社交类网站开发需求分析/培训机构咨询

1. 问题描述：

给你一个有向无环图 ， n 个节点编号为 0 到 n-1 ，以及一个边数组 edges ，其中 edges[i] = [fromi, toi] 表示一条从点  fromi 到点 toi 的有向边。
找到最小的点集使得从这些点出发能到达图中所有点。题目保证解存在且唯一。
你可以以任意顺序返回这些节点编号。

示例 1：

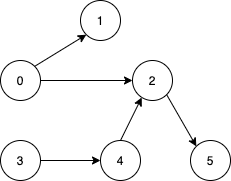
输入：n = 6, edges = [[0,1],[0,2],[2,5],[3,4],[4,2]]
输出：[0,3]
解释：从单个节点出发无法到达所有节点。从 0 出发我们可以到达 [0,1,2,5] 。从 3 出发我们可以到达 [3,4,2,5] 。所以我们输出 [0,3] 。

示例 2：

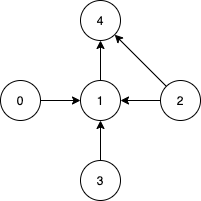
输入：n = 5, edges = [[0,1],[2,1],[3,1],[1,4],[2,4]]
输出：[0,2,3]
解释：注意到节点 0，3 和 2 无法从其他节点到达，所以我们必须将它们包含在结果点集中，这些点都能到达节点 1 和 4 。

提示：

2 <= n <= 10^5
1 <= edges.length <= min(10^5, n * (n - 1) / 2)
edges[i].length == 2
0 <= fromi, toi < n
所有点对 (fromi, toi) 互不相同

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-number-of-vertices-to-reach-all-nodes

2. 思路分析：

一开始感觉是dfs，但是仔细分析题目并不是而且使用dfs思路解决的话不仅复杂而且肯定超时，仔细观察题目给出的图以及测试用例可以发现最小点集都是由入度为0的节点组成的，并且入度为0的节点都是只能够通过自身才能够访问到的，所以入度为0的节点一定是构成最小点集的，看出这一点其实题目就非常好解决了，我们只需要遍历一遍边数组 edges，使用列表统计对应节点的入度，然后遍历列表找出入度为0的节点即可

3. 代码如下：

from typing import Listclass Solution:def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:indegree = [0] * (n)for edge in edges:indegree[edge[1]] += 1res = list()for i in range(n):if not indegree[i]: res.append(i)return res

官方代码：

官方代码使用的是set来记录两个节点的有向边的终点，记录边的终点肯定不是入度为0的节点，最后在[0:n]的范围内找出set中的元素即可（入度为0的节点）

class Solution:def findSmallestSetOfVertices(self, n: int, edges: List[List[int]]) -> List[int]:endSet = set(y for x, y in edges)ans = [i for i in range(n) if i not in endSet]return ans