网站设计要如何做支付功能/外包网络推广公司

引言

2006年的一篇论文《Map-Reduce for Machine Learning on Multicore》[1]在PAC(probably approximate correct)理论和SQL(Statistical Query Learning)[2]理论的框架下，指出了“求和形式算法”可以自然的利用多CPU并行训练（也可以推广到MapReduce编程范式下并行训练）。我们见到的绝大多数使用MapReduce进行训练的模型，都可以归结到这篇论文中提出的形式，它们本质上对于算法本身没有进行任何修改，只是将计算的数据集合进行了一定的拆分。
另外一类的并行训练不依赖MapReduce，例如XGBoost和LightGBM的集群训练模式。这些并行训练本质上是将模型训练过程中的某些方便并行化的步骤做了特殊处理，同样不会修改算法本身。这一类并行算法非常依赖于工程实现。
不同于上述的方式，本文分享的是一种基于微分方程稳定性点的分布式算法：Zero-Gradient-Sum（梯度和零）[3]算法。该算法适用于求和形式的凸问题。同样，这种训练方法不改变算法本身，并且有较优秀的效率，较少的网络IO，以及完备的理论基础。ZGS是一种隐私算法，分布式计算时不同节点之间不交换原始数据，可以使用在医疗数据、金融数据的模型训练场景。经过推广的ZGS在不同类型的网络拓扑结构上(有向图,无向图),不同类型的数据分片上(按行分布或按列分布)以及连续时间和离散时间上均有较为成熟的理论,有很强的适用范围.

问题描述

ZGS适用于如下形式的问题:
$$x^{\ast }\in \underset{x}{\mathrm{argmin}}\sum _{i=1}^N{f}_i(x)\text{\hspace{1em}(1)}$$
其中$f_i$均为可二次求导的凸函数,并且是局部李普希兹的,$N$表示有N个计算节点,$x^{\ast }$是使得${\sum }_{i=1}^N{f}_i(x)$最小的全局最优解.

举个例子,径向基网络(Radial Basis Function Network，RBFN)就满足上述的形式.

我们定义RBFN的损失函数
$$L=||y-Hw|{|}^2+\sigma ||w|{|}^2/2\text{\hspace{1em}(2)}$$
其中$y=[y_1,...,y_N{]}^T$,$w=[w_1,....,w_L{]}^T$
$$H={\left[\begin{array}{ccc}\phi (||x_1-c_1||)& \dots & \phi (||x1-c_L||)\\ ⋮& \ddots & ⋮\\ \phi (||x_N-c_1||)& \dots & \phi (||xN-c_L||)\end{array}\right]}_{N\times L}\text{\hspace{1em}(3)}$$
当径向基函数中$x_i$确定后, 网络的优化即为计算$w$,显然,RBF的损失函数是一个二阶连续的凸函数,满足ZGS可分布式条件.

算法

ZGS的算法最早提出被用于解决无向通信网络中有固定拓扑结构的无约束且可分的凸优化问题.算法表达式如下:
$$\{\begin{array}{r}su{m}_{i=1}^V\nabla f_i(x)=0\\ x_i(0)=x_i^{\ast }\end{array}\text{\hspace{1em}(4)}$$
其中$x_i^{\ast }$表示节点i上的局部最优解.这表示,ZGS将数据分散的存储在不同的节点上,再迭代求解.

例.使用ZGS对RBFN进行训练.

根据公式(2),可以容易求得RBFN损失函数关于$w_i(k)$的导数:
$$\nabla L_i(w_i(k))=(H_i^T{H}_i+{\sigma }_i{I}_L)w_i(k)-H_i^T{y}_i\text{\hspace{1em}(5)}$$
根据ZGS算法,可以得到$w(k)$的迭代式:
$$\{\begin{array}{r}{w}_i(k+1)=w_i(k)+\gamma (H_i^T{H}_i+{\sigma }_i{I}_L{)}^{-1}su{m}_{j\in {\mathbb{N}}_i}{a}_{i}j(w_j(k)-w_i(k))\\ w_i(0)=w_i^{\ast }=(H_i^T{H}_i+{\sigma }_i{I}_L{)}^{-}1H_i^T{y}_i\end{array}\text{\hspace{1em}(6)}$$
进一步,写成矩阵形式:
$$\{\begin{array}{r}W(k+1)=W(k)-\gamma (H^{T}H+\sigma \otimes I_L{)}^{-1}(\mathbb{L}\otimes I)W(k)+W(k)\\ W(0)=W^{\ast }=(H^{T}H+\sigma \otimes I_L{)}^{-1}{H}^{T}y\end{array}\text{\hspace{1em}(7)}$$
其中, $W(k)=[w_1^T(k),w_2^T(k),...,w_V^T(k){]}^T,H=diag{H}_1,H_2,...,H_V,\sigma =diag{\sigma }_1,{\sigma }_2,...,{\sigma }_V$,${\sigma }_i,\gamma$都是可以调的参数.$V$代表分布式拓扑图里的节点集合,$\mathbb{L}$是网络拓扑图的拉普拉斯矩阵.

算法推导

引理1:

强图二次可导的函数满足以下不等式
$$\begin{gathered} f(y)-f(x)-\nabla f(x{)}^T(y-x)\ge \frac{\theta }{2}||y-x|{|}^2 \\ (\nabla f(y)-\nabla f(x){)}^T(y-x)\ge \theta ||y-x|{|}^2 \\ {\nabla }^{2}f(x)\ge \theta I_n\text{\hspace{1em}(8)} \end{gathered}$$
等价的,有
$$\begin{gathered} f(y)-f(x)-\nabla f(x{)}^T(y-x)\le \frac{\Theta }{2}||y-x|{|}^2 \\ (\nabla f(y)-\nabla f(x){)}^T(y-x)\le \Theta ||y-x|{|}^2 \\ {\nabla }^{2}f(x)\le \Theta I_n\text{\hspace{1em}(9)} \end{gathered}$$
引理2:

Lyapunov稳定性分析可以用来确定一个微分方程的稳定性.

对于一个系统,如果平衡状态受到扰动后,任然停留在稳定状态附近,则称为该稳定状态在Lyapunov定义下是稳定的.

如果平衡状态在受到扰动后,最终都会收敛到稳定状态,则称为渐进稳定的.

如果在稳定状态受到 任何扰动 后,最终都会收敛到稳定状态,则称为 大范围内渐进稳定的.

算法推导:

我们的目的是构造一个连续时间的分布式算法:
$$\begin{gathered} {\dot{x}}_i(t)={\phi }_i(x_i(t),x_{Ni}(t);f_i,f_{Ni}) \\ {x}_i(0)=x_i^{\ast }(f_i,f_{Ni})\text{\hspace{1em}(10)} \end{gathered}$$
其中下标中带有N的表示i节点的邻接节点集合.$\dot{x}$表示x的一阶导数.对于这样的微分方程,我们希望他是稳定的,在一定的初值条件下最终能收敛到我们期望的状态.

通过f构造一个Lyapunov方程:
$$V(x)=su{m}_{i\in V}{f}_i(x^{\ast })-f_i(x_i{)}^T(x^{\ast }-x_i)\text{\hspace{1em}(11)}$$
当f为二阶可求导并且强凸时,根据公式(8)易知:
$$\begin{gathered} V(x)\ge su{m}_{i\in V}\frac{{\theta }_i}{2}||x^{\ast }-x_i|{|}^2\ge 0\forall xin{R}^{nN} \\ V(x)\to \infty whenx\to \infty \text{\hspace{1em}(12)} \end{gathered}$$
因此,我们构造的方程是一个合法的Lyapunov方程(该方程取值大于等于0,且当x趋于无穷大时方程趋于无穷大,可以用来刻画系统的能量状态).

对公式(11)做对时间t的求导,可以得到:
$$\dot{V}(x(t))=\sum _{i\in V}(x_t(t)-x^{\ast }){\nabla }^2{f}_i(x_i(t)){\phi }_i(x_i(t),x_{N_i};f_i,f_{Ni})\text{\hspace{1em}(13)}$$
根据问题描述中的假设,每个$\phi$都是局部李普希兹的.$V^{\prime }$是连续的.并且,显然的$V^{\prime }(x^{\ast })=0$.因此,若果能到找到合适的$\phi$使得
$$\sum _{i\in V}(x_t(t)-x^{\ast }){\nabla }^2{f}_i(x_i(t)){\phi }_i(x_i(t),x_{N_i};f_i,f_{Ni})<0,\forall x\ne x^{\ast }\text{\hspace{1em}(14)}$$
那么$V^{\prime }$将在所有非$x^{\ast }$处小于0,整个系统将是Lyapunov渐进稳定的.

但是这样的$\phi$很难构造.首先$x^{\ast }$对于每一个分布式计算节点都是未知的(如果已知那么问题已经得到了最优解).同时,每个节点在计算$\phi$时只能利用到自己的$f_i$和$f_{Ni}$.因此我们不可以让$\phi$ 和$x^{\ast }$关联,例如令$\phi =x^{\ast }-x$.

为了构造合适的$\phi$,引入两个定义
agreementsetA={(y1,y2,...,yN)∈RnN:y1=y2=...=yN}(15)agreement\ set\ \ \ \mathscr{A}=\{(y_1,y_2,...,y_N) \in \mathbb{R}^{nN}:y_1=y_2=...=y_N\} \tag {15} agreement set   A={(y1​,y2​,...,yN​)∈RnN:y1​=y2​=...=yN​}(15)

zero−gradient−summanifoldM={(y1,y2,...,yN)∈RnN:sumi∈V∇fi(yi)=0}(16)zero-gradient-sum\ manifold\ \ \mathscr{M}=\{(y_1,y_2,...,y_N) \in \mathbb{R}^{nN}:sum_{i \in V}\nabla f_i(y_i)=0\} \tag {16} zero−gradient−sum manifold  M={(y1​,y2​,...,yN​)∈RnN:sumi∈V​∇fi​(yi​)=0}(16)

此时$\mathcal{M}$实际上就是一个流形,它的自由度是N-1.有$x^{\ast }\in \mathcal{A}$,$x^{\ast }\in \mathcal{M}$. 又因为
$$\forall xin\mathcal{A}\cap \mathcal{M}\to x=x^{\ast }\text{\hspace{1em}(17)}$$
所以A∩M={x∗}\mathscr{A} \cap \mathscr{M} = \{x^*\}A∩M={x∗}

接下来,在以上两个定义的基础上,给出以下的方法:

条件(14)确保了x沿着任意一条轨迹都将收敛到稳定状态,但这不是必须的.我们只要找出一条轨迹,在这个轨迹上x始终满足(14),那么x沿着这一条轨迹就可以收敛到稳定状态.

观察公式(13),可以得出
$$\dot{V}(x(t))={\Phi }_1(x(t)-x^{\ast T}{\Phi }_2(x(t))\forall t\ge 0\text{\hspace{1em}(18)}$$

.如果我们可以让${\Phi }_2=0$,那么$\dot{(}V)$就会与$x^{\ast }$无关.即需要:
$$\sum {\nabla }^2{f}_i(x_i(t)){\phi }_i(x_i(t),x_{N_i};f_i,f_{Ni})=0\text{\hspace{1em}(19)}$$
于是$\dot{(}V)$变成:
$$\dot{V}(x(t))=\sum _{i\in V}{x}_t(t){\nabla }^2{f}_i(x_i(t)){\phi }_i(x_i(t),x_{N_i};f_i,f_{Ni})\text{\hspace{1em}(20)}$$
这时只要让公式(20)小于0,我们的算法就会收敛.注意到公式(19)和假设(10),我们得到:
$$\frac{d}{dt}\sum _{i\in V}\nabla f_i(x_i(t))=\sum _{i\in V}{\nabla }^2{f}_i(x_i(t))\dot{x_i}(t)=0\text{\hspace{1em}(21)}$$
如果要满足
$$\underset{t\to \infty }{\lim }x(t)=x^{\ast }\text{\hspace{1em}(21)}$$
那么由(21)知,应有:
$$\underset{t\to \infty }{\lim }\frac{d}{dt}\sum _{i\in V}\nabla f_i(x_i(t))=\frac{d}{dt}\sum _{i\in V}\nabla f_i(\underset{t\to \infty }{\lim }{x}_i(t))=\sum _{i\in V}\nabla f_i(x^{\ast })=\nabla F(x^{\ast })=0\text{\hspace{1em}(22)}$$

也就是说,在迭代过程中,每个节点的x梯度和应该始终保持为0. 这里,可以导出初值条件, 所有节点的初值可以这样设置:每个节点的x是当前节点的最优解.(这是满足条件的轨迹上的一个点.)当然这不是唯一可选的初值,但确实最容易构造的初值.

上图解释了前边的推理过程.首先看左图,如果公式(14)除了初值以外均小于0,那么我们从任意的初始位置出发(图中给了3个绿色的点,代表随机选择的三个初值),都可以逐渐收敛到中心稳定的红色点位置. 但实际上,我们只要找出一条确定的收敛路径即可.有图中蓝色的线就只这一条确定的路线.在这条路径上分布式计算节点的梯度和始终都是0.这条路径上有一个特殊的点,很容易找到,也就是每个分布式计算点的本地最优解.

到此为止,只剩$\phi$没有确定了.观察公式(20),$\phi$总是左乘一个非奇异的${\nabla }^2{f}_i(x_i(t))$,所以我们这样构造$\phi$:
$${\phi }_i=({\nabla }^2{f}_i(x_i){)}^{-1}{\varphi }_i(x_i,x_{Ni};f_i,f_{Ni})\text{\hspace{1em}(23)}$$
根据(20)应该小于0,结合公式(19),有:
$$\begin{gathered} \sum _{i\in V}{\varphi }_i=0\forall x\in {\mathbb{R}}^{n\mathbb{N}} \\ \sum _{i\in V}{x}_i^T{\varphi }_i<0\forall x\in {\mathbb{R}}^{n\mathbb{N}}-\mathcal{A}\text{\hspace{1em}(24)} \end{gathered}$$
这时,x的迭代表达式可以写成:
$$\begin{gathered} \dot{x_t}(t)=({\nabla }^2{f}_i(x_i(t)){)}^{-1}\sum _{j\in N_i}{\varphi }_{ij}(x_i(t),x_j(t);f_i.f_j) \\ {\varphi }_i=\sum _{j\in N_i}{\varphi }_{ij}\text{\hspace{1em}(25)} \end{gathered}$$
只要让
$${\varphi }_{ij}=-{\varphi }_{ji}\text{\hspace{1em}(26)}$$
公式(24)的第一个等式就可以成立.带入(24)的不等式,得到
$$\sum _{i\in V}{x}_i^T{\varphi }_i=\frac{1}{2}\sum _{i\in V}\sum _{j\in N_i}(x_i-x_j{)}^T{\varphi }_{ij}\text{\hspace{1em}(27)}$$
对于$\forall x\in {\mathbb{R}}^{nN}-\mathcal{A}$, (27)中的$x_i-x_j$都不等于0.于是(24)不等式成立的条件可以是:
$$(y-z{)}^T{\varphi }_{ij}(y.z;f_i,f_j)<0,\forall i\in v,\forall j\in N_i,\forall y,z\in {\mathcal{R}}^n,y\ne z\text{\hspace{1em}(28)}$$
此时我们只需要考虑图中的一部分节点,对于节点i,需要满足(28)成立,但对于节点j,只要简单的利用(26)确定$\varphi$即可.

以下给出一些合适的$\varphi$的例子.

Example1:
$$\begin{gathered} {\varphi }_{ij}(y,z;f_i,f_j)=({\psi }_{ij1}(y_1,z_1),{\psi }_{ij2}(y_2,z_2),...,{\psi }_{ijn}(y_n,z_n)) \\ {\psi }_{ijk}(y_k,z_k)=-{\psi }_{ijk}(z_k,y_k) \\ (y_k-z_k){\psi }_{ijk}(y_k,z_l)<0\forall y_k\ne z_k \end{gathered}$$

$$\begin{gathered} e.g.{\varphi }_{ijk}(y_k,z_k)=tanh(z_k-y_k) \\ e.g.{\varphi }_{ijk}(y_k,z_k)=\frac{z_k-y_k}{1+y_k^2} \end{gathered}$$

Example2:
ϕij(y,z;fi,fj)=∇g{i,j}(z)−∇g{i,j}(y)\phi_{ij}(y,z;f_i,f_j)=\nabla g\{i,j\}(z)-\nabla g\{i,j\}(y) ϕij​(y,z;fi​,fj​)=∇g{i,j}(z)−∇g{i,j}(y)
其中g{i,j}g\{i,j\}g{i,j}可以是任意的二阶连续可导并且局部强凸的函数.例如
g{i,j}(y)=12yTA{i,j}yg\{i,j\}(y)=\frac{1}{2}y^TA\{i,j\}y g{i,j}(y)=21​yTA{i,j}y
其中A是任意的对称正定矩阵.

实验

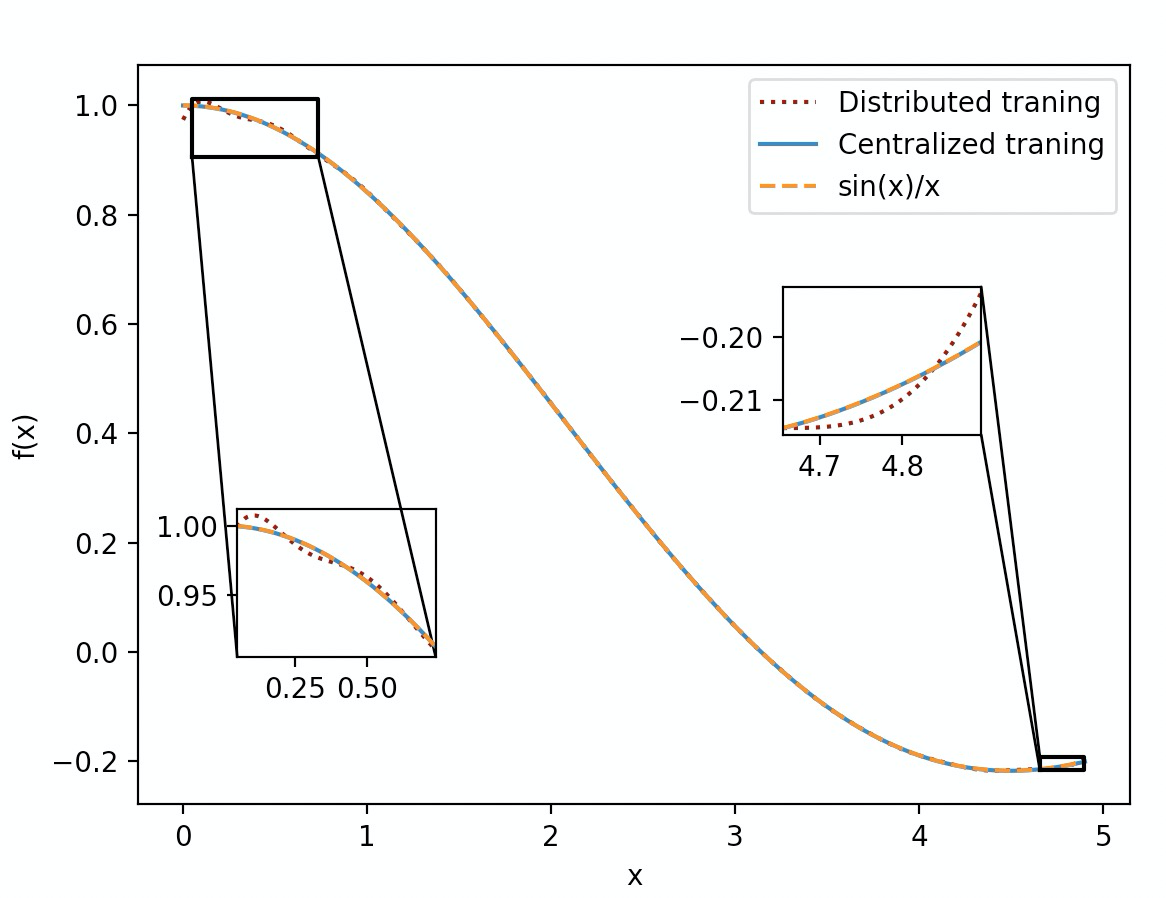
利用算法描述里的公式(6),使用10000个样本在macbook上进行了实验.测试函数为sin(x)/x

参考文献

[1]Cheng-Tao Chu,Sang Kyun Kim,Yi-An Lin, et al.Map-Reduce for Machine Learning on Multicore[C].//Advances in neural information processing systems 19 :.2007:281-288.

[2]Diakonikolas I, Kane D M, Kontonis V, et al. Algorithms and sq lower bounds for pac learning one-hidden-layer relu networks[C]//Conference on Learning Theory. PMLR, 2020: 1514-1539.

[3]Lu J, Tang C Y. Zero-gradient-sum algorithms for distributed convex optimization: The continuous-time case[J]. IEEE Transactions on Automatic Control, 2012, 57(9): 2348-2354.