去年的比赛了,然而今天才改好。
总体难度适中,有大佬AK。
主要是自己SB第二题没想出来,然后又是可怜的100来分。
T1 一道二分+数学的题目。
我们可以二分叫的次数,然后用公式(等差数列,公差都是zi)算一个最大的可行的数目。
最后把多余的加上去即可。
注意当xi,yi都等于0的情况。
CODE
#include<cstdio> #include<cmath> using namespace std; typedef long long LL; LL ans,n,t,t_2,t_s,x,y,z,res,l,r,mid,temp; inline void read(LL &x) {x=0; char ch=getchar();while (ch<'0'||ch>'9') ch=getchar();while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); } int main() {freopen("brute.in","r",stdin); freopen("brute.out","w",stdout); read(n); read(t); t_2=t*2;while (n--){read(x); read(y); read(z);l=1; if (x+y) r=t/(x+y); else r=(LL)sqrt(t_2/z)+1; temp=2*x+2*y;while (l<=r){mid=l+r>>1;if (mid*(temp+mid*z-z)<=t_2) res=mid,l=mid+1; else r=mid-1;}ans+=res*(2*y+z*res-z)/2;t_s=t-res*(temp+res*z-z)/2-x;if (t_s>0) ans+=t_s;}printf("%lld",ans);return 0; }
T2 标算用了神奇的。。。数据结构来打。
然而当时A了这道题的都是用超级简单的方法水过的。
现在只讨论玄学算法(即超级水过的算法)。
由于题目不要求分别输出每一次的值,所以我们只需要先把全部操作做完,最后1次DFS遍历一下每个点一共访问了几次。
第1次操作ans+1; 第2次 ans+2; 第3次 ans+3; 第n次 ans+n;
然后又是玄学的等差数列求和即可。ans+=(n+1)*n/2;
CODE
#include<cstdio> #include<vector> using namespace std; typedef long long LL; const int N=100005; vector <LL> a[N]; LL n,m,i,x,ans,t[N],f[N]; struct io {char op[1 << 26] , * s;io(){freopen( "chiye.in" , "r" , stdin );freopen( "chiye.out" , "w" , stdout );fread( s = op , 1 , 1 << 26 , stdin );}inline void read(LL &u){u = 0;while( * s < 48 ) s++;while( * s > 32 )u = u * 10 + * s++ - 48;} } ip; #define read ip.read inline void dfs(int k) {f[k]+=t[k];for (int i=0;i<a[k].size();++i)f[k]+=t[a[k][i]],f[a[k][i]]+=t[k],dfs(a[k][i]); } int main() {read(n); read(m);for (i=2;i<=n;++i){read(x);a[x].push_back(i);}while (m--){read(x);t[x]++;}dfs(1);for (i=1;i<=n;++i)ans+=f[i]*(f[i]+1)/2;printf("%lld",ans);return 0; }
(fread模板是免费提供的)
T3 Tarjan缩点+树形DP
就这道题改了很久,到现在还是因为不会Tarjan缩点(打了DFS)TLE了4个点。
首先前30分想怎么暴力怎么暴力。
然后发现因为这个图只有简单环,所以左右的点可以分成2种:圆点和方点。
简单地说,圆点就是原来的图中不包括在任何一个环中的点;方点就是把一个简单环缩成的一个点。如下图:
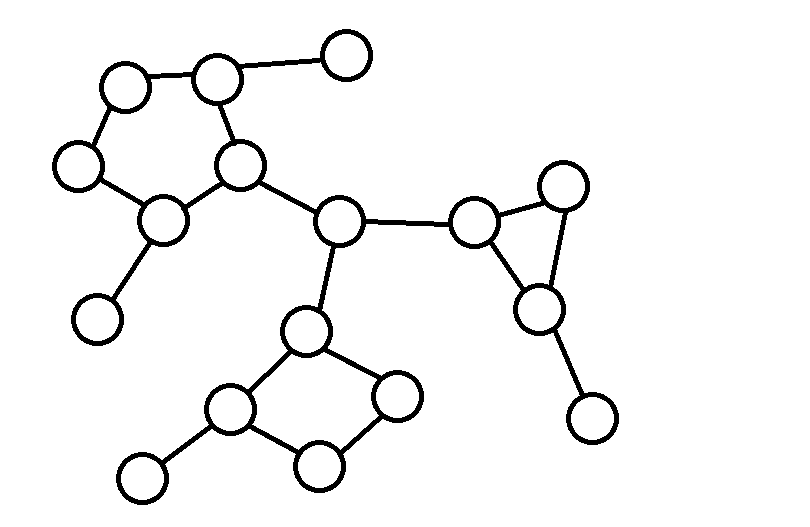
变成
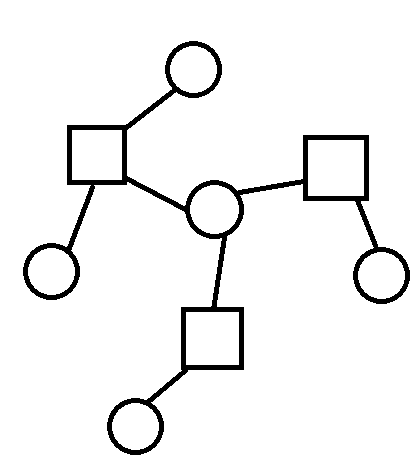
然后我们发现一个眼镜的两边都是方点,如果两个端点确定,那么这两个点可以组成的眼镜数量就是2^(两个端点之间的方点个数);
接下来又有50——70分可以暴力DFS了。
如果想得满分,就得考虑树形DP,设f[x]为以x为根的子树(包括x)一共有多少“一半的眼镜”(即只有一个端点的)
然后状态转移 :
f[x] = Σ( f[ son[x] ] );
如果x是圆点,则f[x]不变
如果x是方点,则f[x] = f[x] * 2 + 1(可以走两次再加上它自己)
每次做的时候更新ans即可。具体看代码。
CODE
#include<cstdio> #include<vector> #include<cstring> using namespace std; const int N=1000005,mod=19260817; vector <int> a[N],b[N]; int n,m,f[N],num[N],pre[N],i,j,tot,x,y; bool kinds[N],vis[N],use[N]; long long ans; inline void read(int &x) {x=0; char ch=getchar();while (ch<'0'||ch>'9') ch=getchar();while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar(); } inline void print(int k) {if (pre[k]) print(pre[k]);num[k]=tot;use[k]=1; } inline void find(int s,int k) {for (int i=0;i<a[k].size();++i)if ((!vis[a[k][i]])&&(!use[a[k][i]])) pre[a[k][i]]=k,vis[a[k][i]]=1,find(s,a[k][i]),vis[a[k][i]]=0; elseif (a[k][i]==s&&a[k][i]!=pre[k]){print(k);kinds[tot]=1;return;} } inline int dp(int k) {vis[k]=1;for (int i=0;i<b[k].size();++i){int now=b[k][i];if (vis[now]) continue;int temp=dp(b[k][i]);ans=(ans+f[k]*(kinds[k]?2ll:1ll)*temp)%mod;f[k]=(f[k]+temp)%mod;}if (kinds[k]) ans=(ans+f[k])%mod,f[k]=(f[k]*2+1)%mod;return f[k]; } int main() {freopen("dark.in","r",stdin); freopen("dark.out","w",stdout);read(n); read(m);for (i=1;i<=m;++i){read(x); read(y);a[x].push_back(y); a[y].push_back(x);}for (i=1;i<=n;++i)if (!use[i]) ++tot,num[i]=tot,use[i]=1,kinds[tot]=0,memset(pre,0,sizeof(pre)),vis[i]=1,find(i,i),vis[i]=0;for (i=1;i<=n;++i)for (j=0;j<a[i].size();++j)if (num[i]!=num[a[i][j]]) b[num[i]].push_back(num[a[i][j]]);dp(1);printf("%lld",ans);return 0; }








