您现在的位置是:主页 > news > 深圳专业制作网站公司吗/友情链接适用网站
深圳专业制作网站公司吗/友情链接适用网站
![]() admin2025/6/24 11:02:34【news】
admin2025/6/24 11:02:34【news】
简介深圳专业制作网站公司吗,友情链接适用网站,邵阳新闻头条今日,erp软件多少钱阅读全文大概需要4.5分钟, 建议先收藏一.什么是箱线图?箱线图(Box Plot)也就是箱须图(BoxWhisker Plot), 它是由一组或多组连续型定量数据的「最小观测值」、第一四分位数、中位数、第三分位数和「最大观测值」来反映数据的分布情况的统计图,因外形似箱子而得名。(…
阅读全文大概需要4.5分钟, 建议先收藏一.什么是箱线图?
箱线图(Box Plot)也就是箱须图(BoxWhisker Plot), 它是由一组或多组连续型定量数据的「最小观测值」、第一四分位数、中位数、第三分位数和「最大观测值」来反映数据的分布情况的统计图,因外形似箱子而得名。(又称盒图,箱图)
数据进行量化处理时分为连续型数据和离散型数据。
像骰子的数字[只能为1-6的整数],汽车的销量[只能为整数]等只能取跨越型数值,称为离散型数据;身高[可以为170cm,180.3cm,190.05cm...]、体重、时间都可以取连续数值的数据称为连续型数据。
箱线图的外形及基本组成:
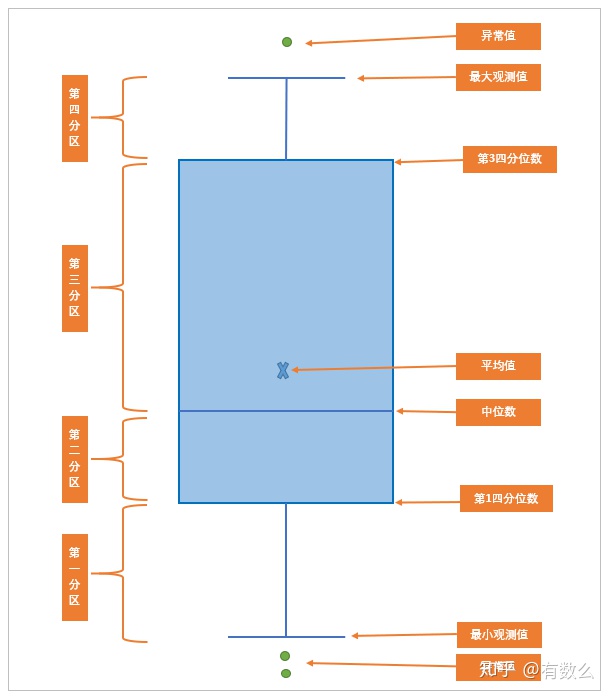
- 数据排序后分成4等份,每份包含25%的数据
- 箱子中包含50%的数据
- 箱子中间的直线代表中位数(median),也就是第2四分位数(Q2)
- 箱子上边缘代表第3四分位数(Q3);下边缘代表第1四分位数数(Q1)
- 最小观测值和最大观测值是除异常值外的最小和最大数据值
- X 代表平均数,异常值用圆圈表示
关于最小,最大观测值的命名问题,为免歧义,文末单独进行了说明
如果要了解箱线图的构成,就必须先了解一些关于数据的代表值的定义,比如说中位数、平均数、四分位数、平均值......
二.数据的代表值
研究数据整体的离散性时,最小值(mimimum),第一四分位数(1st quartile)、中位数(median)、第三四分位数(3rd quartile)、最大值(maximum)称为"5大要数", 分别加以说明。
为了方便说明,假设我们在上海调研12位IT从业者,工作多久后会年薪过百万,得到样本数据T:{5, 7, 6, 28, 8, 12, 11, 13, 12, 14, 16, 15},数据单位为年。(数据仅供参考,切莫自我带入!)
1. 最大值(Max),最小值(Min):数据排序后,位于数据的两端
首先样本T从小到大排序后为{5, 6, 7, 8, 11, 12, 12, 13, 14, 15, 16, 28} ;很明显样本的最大值为28,最小值为4。
2. 中位数:将数据按大小排列后,位于最中间的值。如数据个数为N,则排序后,中位数在(N+1)/2 位置上。
- 当数据个数为奇数:
例如数据组A:{10, 20, 50, 50, 70, 60, 90},包括7个数,排序后为:{90, 70, 60, 50, 50, 20, 10} , 中位数位置:(7+1)/2 = 4, 即中位数为50。
- 当数据个数为偶数:
例如数据组B:{25, 40, 30, 42, 55, 60, 50, 70},包括8个数,排序后为:{70, 60, 55, 50, 42, 40, 30, 25},中位数位置:(8+1)/2 = 4.5, 则B组的中位数为: (50+42)/2 = 46。
对于样本T,中位数位置:(12+1)/2 = 6.5, 中位数等于 (12 + 12)/2 = 6。
3. 四分位数:将数据按大小排序后,分成4等分后,处于3个分割点上的数为四分位数;这三个四分位数按照从小到大的顺序分别为第一四分位数,第二四分位数和第三四分位数。
图示:
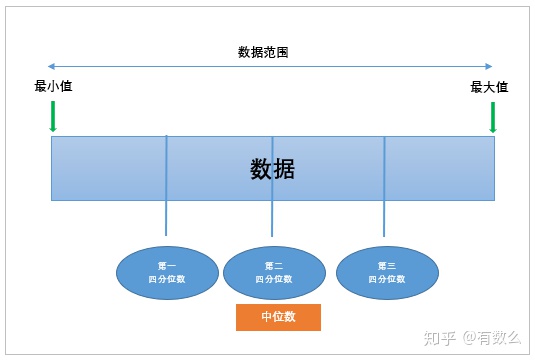
- 第一四分位数(Q1),又称“较小四分位数”,等于样本数据从小到大排序后第25%的数字
- 第二四分位数(Q2),又称“中位数”,等于样本数据从小到大排序后第50%的数字
- 第三四分位数(Q3),又称“较大四分位数”,等于样本数据从小到大排序后第75%的数字
- 四分位距(IQR: InterQuartile Range) = Q3-Q1
>>如何确定四分位数<<
对于四分位数的确定有两种方法,一种是基于「N+1」基础, 另一种是基于「N-1」基础,这里N代表数据的个数。
>a. N+1
EXCEL 的函数 "QUARTILE.EXC" 就是基于此, 这里EXC: Exclusive
- Q1的位置=(n+1) * 0.25
- Q2的位置=(n+1) * 0.5
- Q3的位置=(n+1) * 0.75
结合样本T,计算如下
Step1:数据从小到大排序
{5, 6, 7, 8, 11, 12, 12, 13, 14, 15, 16, 28}
Step2:计算Q1
Q1位置 = (12+1) * 0.25 = 3.25 , 数据位于第3和第4数据之间,靠近第3数据
相当于第三,第四数据的权重分别为0.75,0.25
Q1 = 7 * 0.75 + 8 * 0.25 = 7.25
Step3:计算Q2
Q2[中位数]位置 = (12+1) * 0.5 = 6.5 , 数据位于第6和第7数据之间,均匀分布
Q2 =12*0.5 + 12*0.5 = 12
Step4:计算Q3
Q3位置 = (12+1) * 0.75 = 9.75 , 数据位于第9和第10数据之间,靠近第10数据
Q3 = 14 * 0.25 + 15 * 0.75 = 14.75
Step5:计算IQR
IQR = Q3 - Q1 = 7.5
>b. N-1
EXCEL 的函数 "QUARTILE.INC" 以及函数 "QUARTILE" 都是基于此, 这里INC: Inclusive
- Q1的位置=1+(n-1) * 0.25
- Q2的位置=1+(n-1) * 0.5
- Q3的位置=1+(n-1) * 0.75
结合样本T,参考如上计算步骤,结果如下:
- Q1 = 7.75
- Q2 = 12
- Q3 = 14.25
- IQR = 6.5
可以看出,方法不同计算出的四分位数结果也不相同,当然采用哪种算法都可以,一般N+1比较常用。
4. 平均值(Mean): 数据的算数/几何平均值
显然,样本T的平均值为 12.25
按照不同四分位数的计算方法,样本T的“5大要数”以及平均数为:

结合语义,我们可以看出(基于四分位数N+1算法):
- 样本中25%的人实现年薪百万,可以在7.25年内达成 (妥妥的王者水平)
- 样本中25%的人实现年薪百万,需要7.25-12年(算的上星耀了)
- 样本中25%的人实现年薪百万,需要12-14.75年(钻石没问题)
- 样本中25%的人实现年薪百万,需要14.75年以上(段位铂金)
- 参照样本,实现年薪百万基本上需要12年左右
- 有一个大神,只用了5年就实现了年薪百万!
- 有一个数据比较奇怪,用了28年实现了年薪百万,与样本中其他数据偏差比较大!
当然了,只要实现年薪百万,那肯定就是黄金水平了!
现在我们已经了解“5大要数”和平均数的计算方法,要绘制完整的箱线图,我们需要继续搞懂箱线图中「最小、最大观测值」以及「异常值」。
三. 箱线图的最小观测值、最大观测值以及异常值
“最小观测值和最大观测值是除异常值外的最小和最大数据值”
这是文章开头,对于最大/最小观测值的定义,要找出观测值,就必须先找到「异常值」,还是拿样本T说明:
T:{5, 7, 6, 28, 8, 12, 11, 13, 12, 14, 16, 15}
前面说过,样本中的"28"这个数据比较奇怪,偏离样本中其他数据,那么这个数据究竟是不是异常值?!
识别异常值[Outliers]的标准:
异常值被定义为小于“Q1-1.5*IQR”或大于"Q3+1.5*IQR"的值
这里「Q1-1.5*IQR」也被称为下限值,这里「Q3+1.5*IQR」也被称为上限值
某些文档中,异常值分为温和异常值(mild outliers) 和 极端异常值(extreme outliers)
「Q1-1.5IQR」也被称为内下限值,「Q3+1.5IQR」也被称为内上限值;
「Q1-3IQR」也被称为外下限值,「Q3+3IQR」也被称为外上限值;
数据落在内限值和外限值之间则称为温和异常值,用"O"标识;
数据落在外限值之外则称为极端异常值,用"*"标识;
非特别说明,温和异常值,极端异常值不予区分,统称异常值。
因此样本T的上下限值为:
- 基于N+1
上限值"maxmum" = 14.75 + 1.5*7.5 = 26
下限值"minmum" = 7.25 - 1.5*7.5 = -4
- 基于N -1
上限值"maxmum" = 14.25 + 1.5*6.5 = 24
下限值"minmum" = 7.75 - 1.5*6.5 = -2
可以看出,无论是基于N+1还是N-1算法,样本中只有数据“28”是异常值。
- 据此,样本T的最小观测值,就是样本的最小值,4
- 据此,样本T的最大观测值,就是出去异常数据"28"外的最大值,16
四. 实例化箱线图
参考样本T:{5, 7, 6, 28, 8, 12, 11, 13, 12, 14, 16, 15}, 按照不同的四分位计算方法,最终得到箱线图的代表数为:

箱线图分别为:
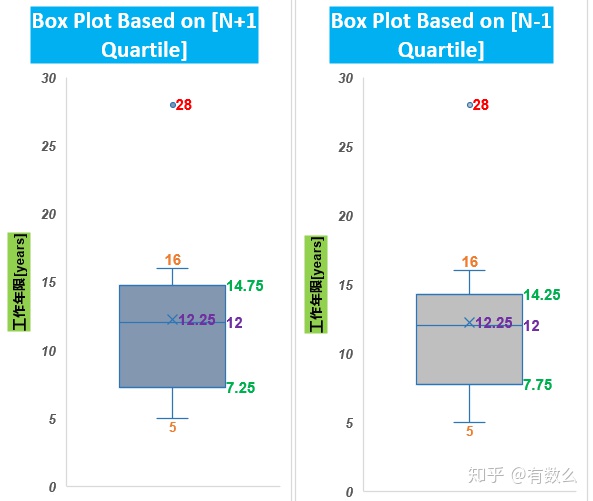
参考箱线图,我们不难得出
- 对于上海IT从业者来说,工作12年-16年左右,最有可能获得百万年薪。
- 两极性,25%的从业者在5-7年可以获得百万年薪,相对应,25%的从业者则需要花费15年以上才能达成这个目标。
正文结束
限于篇幅,为更好的阅读体验,EXCEL 绘制箱线图的方法写在下篇
看完了正文,其实最容易产生误解的就是关于箱线图中的最小观测值和最大观测值,事实上这两个术语确实有"篡改","自造"的嫌疑,我找相关资料的时候,确实也看到了不同的箱线结构,这里加以说明。
- 最小观测值为数据最小值,最大观测值为数据最大值
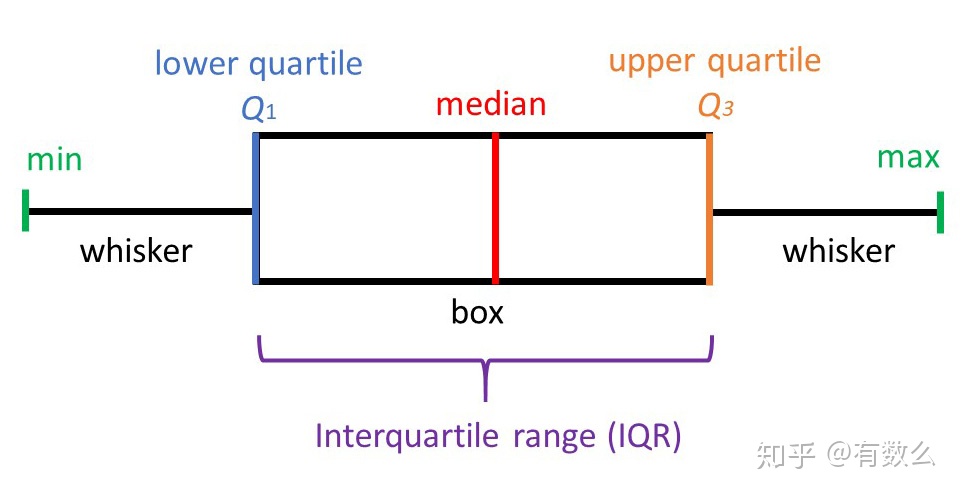
如上箱线图的问题在于,用数据的最大最小值代替了观察值,一旦数据中有异常值,就会产生歧义,比如正文中的样本T, 异常值"28", 就会代替最大观测值。
换句话说,如上箱线图适用于数据没有异常值的情况
这就有意思了,很多时候我们绘制箱线图的目的就是确定数据有没有异常值!
2. 最小观测值为数据的下限值,最大观测值为数据上限值
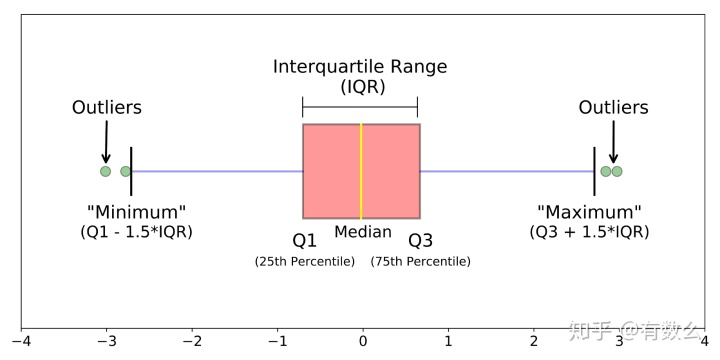
如上箱线图的问题是,虽然用上下限值(内限值)取代了原本的最小、最大观测值,虽然依然可以展示异常值,但是样本数据的最大值,最小值这些关键代表数却无法展示。
换句话说,就是少了箱线图本应具备的数据信息,真实应用中,不适用!
最后,觉得有用,点个赞再走~~
热情洋溢的欢迎转载,注明出处哦!








