深圳网页制作服务商/站长工具seo

1、基本思想

采用一对平行的数组，一个存储键一个存储值
实现的核心是 rank() 方法，它返回表中小于给定键的键的数量。

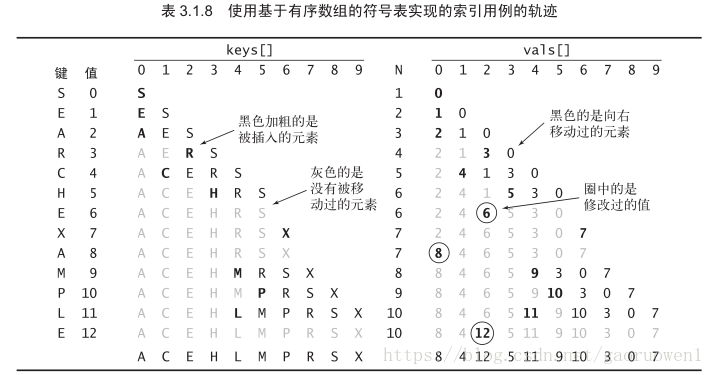
2、算法实现

二分查找法：将被查找的键和子数组的中间键比较。如果被查找的键小于中间键，就在左子数组中继续查找，如果大于就在右子数组中继续查找，否则中间键就是我们要找的键。

实现 rank() 采用了二分查找法，rank()性质如下：
如果表中存在该键，rank() 返回该键的位置，也就是表中小于它的键的数量
如果表中不存在该键，rank() 仍返回表中小于它的键的数量

/*基于递归的二分查找*/
public int rank(Key key,int lo,int hi)
{                        if(hi<lo)return lo;int mid = lo+(hi-lo)/2;int cmp = key.compareTo(keys[mid]);if(cmp > 0)return rank(key, mid+1, hi);else if(cmp < 0)return rank(key, lo, mid-1);else return mid;
}

/*基于迭代的二分查找*/
public int rank(Key key)
{                  int lo=0, hi=N-1;while(lo <= hi){int mid = (lo+hi)/2;int cmp = key.compareTo(keys[mid]);if(cmp < 0)hi = mid-1;else if(cmp > 0)lo = mid+1;else return mid;}return lo;
}

3、基于二分查找的有序符号表

/** 算法3.2 二分查找（基于有序数组）* 数据结构是一对平行的数组，一个存储键一个存储值,* 并在构造函数中将它们转化回 Key[] 和 Value[] 
*/
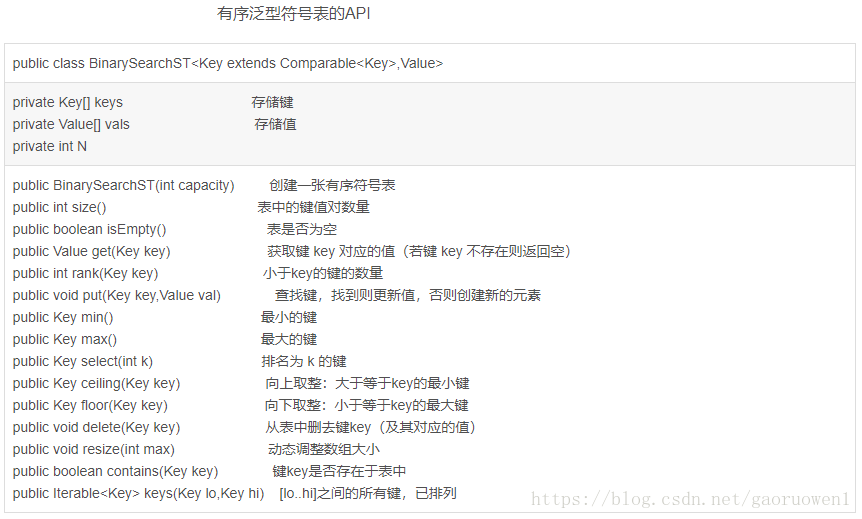
public class BinarySearchST<Key extends Comparable<Key>,Value>
{private Key[] keys;private Value[] vals;private int N;public BinarySearchST(int capacity){keys=(Key[]) new Comparable[capacity];vals=(Value[]) new Object[capacity];}//rank()方法实现了二分查找，它返回表中小于给定键的键的数量public int rank(Key key)public Value get(Key key){if(isEmpty())return null;int i = rank(key);if(i<N && keys[i].compareTo(key)==0)return vals[i];else return null;}public void put(Key key,Value val){                                       int i=rank(key);if(i<N && keys[i].compareTo(key)==0){vals[i]=val;return;}for(int j=N; j>i; j--){keys[j]=keys[j-1];vals[j]=vals[j-1];}keys[i]=key;vals[i]=val;N++;if(N == keys.length)resize(2*keys.length);   //扩充数组大小}public void delete(Key key)  {if(!contains(key))return;int i=rank(key);for(int j=i; j+1<N; j++){keys[j]=keys[j+1];vals[j]=vals[j+1];}N--;if(N>0 && N==keys.length/4)resize(keys.length/2);    //缩小数组大小}public void resize(int max){        //动态调整数组大小Key[] kt = (Key[])new Comparable[max];Value[] vt = (Value[])new Object[max];for(int i=0; i<N; i++){kt[i]=keys[i];vt[i]=vals[i];}keys=kt;vals=vt;}public int size(){ return N; }public boolean isEmpty(){ return N==0; }public Key min(){ return keys[0]; }public Key max(){ return keys[N-1]; }public Key select(int k){ return keys[k]; }public Key ceiling(Key key){   //向上取整：大于等于key的最小键int i=rank(key);return keys[i];}public Key floor(Key key){    //向下取整：小于等于key的最大键int i=rank(key);if(i<N && key.compareTo(keys[i])==0)return keys[i];return keys[i-1];}public boolean contains(Key key){      //键key是否存在于表中int i=rank(key);if(i<N && keys[i].compareTo(key)==0)return true;return false;}public Iterable<Key> keys(Key lo,Key hi){    //[lo..hi]之间的所有键，已排列Queue<Key> q=new Queue<Key>();for(int i=rank(lo); i<rank(hi); i++)q.enqueue(keys[i]);if(contains(hi))q.enqueue(keys[rank(hi)]);return q;}
}

附：可参考例子-记频器

4、性能分析

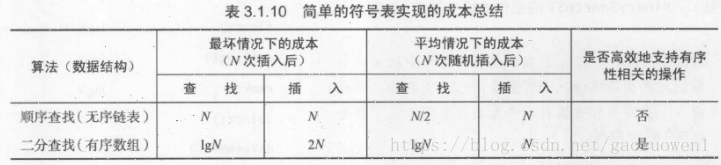
5、顺序查找和二分查找比较

一般情况下，二分查找都比顺序查找快得多，它也是众多实际应用程序的最佳选择。
当然，二分查找也不适合很多应用。例如，它无法处理Leipzig Corpora数据库，因为查找和插入操作是混合进行的，而且符号表也太大了。如我们所强调的那样，现代应用需要同时能够支持高效的 查找 和 插入 两种操作的符号表实现。也就是说，我们需要在构造庞大的符号表的同时能够任意插入（也许还有删除）键值对，同时也要能够完成查找操作。

所以，我们现在核心的问题在于能否找到同时保证查找和插入操作都是对数级别的算法和数据结构。
要支持高效的插入操作，似乎需要一种链式结构。但单链表无法使用二分查找，因为二分查找的高效来自于能够快速通过索引取得任何子数组的中间元素。
为了将二分查找的效率和链表的灵活性结合起来，我们需要更加复杂的数据结构。能够同时拥有两者的就是二叉查找树。