南京网站设计制作排名/seo一般包括哪些内容

一、 题目描述

已有方法 rand7 可生成 1 到 7 范围内的均匀随机整数，试写一个方法 rand10 生成 1 到 10 范围内的均匀随机整数。

不要使用系统的 Math.random() 方法。

示例 1:

输入: 1
输出: [7]

 示例 2:

输入: 2
输出: [8,4]

 示例 3:

输入: 3
输出: [8,1,10]

提示:

1. rand7 已定义。
2. 传入参数: n 表示 rand10 的调用次数。

进阶:

1. rand7()调用次数的 期望值 是多少 ?
2. 你能否尽量少调用 rand7() ?

二、实现思路以及代码

刚开始做这种类型的题目，毫无思绪，参考的某大神的题解，见下：

https://leetcode-cn.com/problems/implement-rand10-using-rand7/solution/cong-zui-ji-chu-de-jiang-qi-ru-he-zuo-dao-jun-yun-/

 1、 (rand_X() - 1) × Y + rand_Y() ==> 可以等概率的生成[1, X * Y]范围的随机数

假设已知rand2()可以均匀的生成[1,2]的随机数，现在想均匀的生成[1,4]的随机数，该如何考虑？

我想如果你也像我一样第一次接触这个问题，那么很可能会这么考虑——令两个rand2()相加，再做一些必要的边角处理。如下：

rand2() + rand2() = ? ==> [2,4]1    +   1     = 21    +   2     = 32    +   1     = 32    +   2     = 4// 为了把生成随机数的范围规约成[1,n]，于是在上一步的结果后减1
(rand2()-1) + rand2() = ? ==> [1,3]0       +   1     = 10       +   2     = 21       +   1     = 21       +   2     = 3

可以看到，使用这种方法处理的结果，最致命的点在于——其生成的结果不是等概率的。在这个简单的例子中，产生2的概率是50%，而产生1和3的概率则分别是25%。原因当然也很好理解，由于某些值会有多种组合，因此仅靠简单的相加处理会导致结果不是等概率的。

因此，我们需要考虑其他的方法了。

仔细观察上面的例子，我们尝试对 (rand2()-1) 这部分乘以 2，改动后如下：

(rand2()-1) × 2 + rand2() = ? ==> [1,3]0            +   1     = 10            +   2     = 22            +   1     = 32            +   2     = 4

神奇的事情发生了，奇怪的知识增加了。通过这样的处理，得到的结果恰是[1,4]的范围，并且每个数都是等概率取到的。因此，使用这种方法，可以通过rand2()实现rand4()。

也许这么处理只是我运气好，而不具有普适性？那就多来尝试几个例子。比如：

(rand9()-1) × 7 + rand7() = resulta               b

 为了表示方便，现将rand9()-1表示为a，将rand7()表示为b。计算过程表示成二维矩阵，如下：

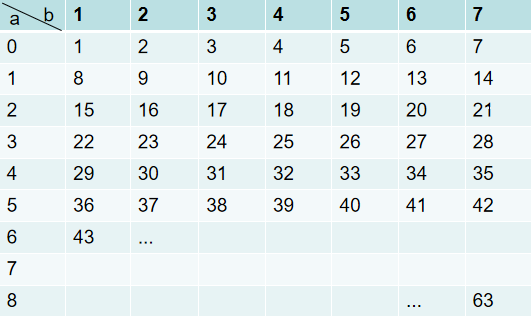
可以看到，这个例子可以等概率的生成[1,63]范围的随机数。再提炼一下，可以得到这样一个规律：

已知 rand_N() 可以等概率的生成[1, N]范围的随机数
那么：
(rand_X() - 1) × Y + rand_Y() ==> 可以等概率的生成[1, X * Y]范围的随机数
即实现了 rand_XY()

2、 通过rand4()来实现rand2()：取余，再加1

那么想到通过rand4()来实现rand2()呢？这个就很简单了，已知rand4()会均匀产生[1,4]的随机数，通过取余，再加1就可以了。如下所示，结果也是等概率的。

rand4() % 2 + 1 = ?1 % 2    + 1 = 22 % 2    + 1 = 13 % 2    + 1 = 24 % 2    + 1 = 1

事实上，只要rand_N()中N是2的倍数，就都可以用来实现rand2()，反之，若N不是2的倍数，则产生的结果不是等概率的。比如：

rand6() % 2 + 1 = ?1 % 2    + 1 = 22 % 2    + 1 = 13 % 2    + 1 = 24 % 2    + 1 = 15 % 2    + 1 = 26 % 2    + 1 = 1rand5() % 2 + 1 = ?1 % 2    + 1 = 22 % 2    + 1 = 13 % 2    + 1 = 24 % 2    + 1 = 15 % 2    + 1 = 2

3、

ok，现在回到本题中。已知rand7()，要求通过rand7()来实现rand10()。

有了前面的分析，要实现rand10()，就需要先实现rand_N()，并且保证N大于10且是10的倍数。这样再通过rand_N() % 10 + 1 就可以得到[1,10]范围的随机数了。

(rand7()-1) × 7 + rand7() ==> rand49()

 但是这样实现的N不是10的倍数啊！这该怎么处理？这里就涉及到了“拒绝采样”的知识了，也就是说，如果某个采样结果不在要求的范围内，则丢弃它。基于上面的这些分析，再回头看下面的代码，想必是不难理解了。

class Solution extends SolBase {public int rand10() {while(true) {int num = (rand7() - 1) * 7 + rand7(); // 等概率生成[1,49]范围的随机数if(num <= 40) return num % 10 + 1; // 拒绝采样，并返回[1,10]范围的随机数}}
}

根据part 1的分析，我们已经知道(rand7() - 1) * 7 + rand7() 等概率生成[1,49]范围的随机数。而由于我们需要的是10的倍数，因此，不得不舍弃掉[41, 49]这9个数。优化的点就始于——我们能否利用这些范围外的数字，以减少丢弃的值，提高命中率总而提高随机数生成效率。

/*** The rand7() API is already defined in the parent class SolBase.* public int rand7();* @return a random integer in the range 1 to 7*/
class Solution extends SolBase {public int rand10() {int a = rand7();//[1,7]以内的随机数int b = rand7();int num = (a - 1) * 7 + b; // rand49if(num <= 40){ // 拒绝采样return num%10+1;}a = num - 40;// rand9：[0,9]b = rand7();//[0,7]num = (a - 1)*7+b; //rand63if(num <= 60){return num%10+1;}a = num -60;//rand3:[1,3]b = rand7();//[0,7]num = (a - 1)* 7+b;// rand21if(num <= 20){return num%10+1;}return 1;}
}