您现在的位置是：主页 > news > 基于php的网站开发毕业论文/北京网站定制公司

基于php的网站开发毕业论文/北京网站定制公司

admin2025/6/13 20:01:22【news】

简介基于php的网站开发毕业论文,北京网站定制公司,怎么做美食团购网站,wordpress用户安全文章目录一、差分介绍与代码模板二、从差分到原数组三、一维差分的应用【区间加】四、一维差分应用拓展【区间加等差单点查询】五、二维差分六、总结一、差分介绍与代码模板如果我们需要维护的数据是“两个相邻数据之差”，这就是差分。令diai−ai−1d_{i}a_{i}-a_…

基于php的网站开发毕业论文,北京网站定制公司,怎么做美食团购网站,wordpress用户安全文章目录一、差分介绍与代码模板二、从差分到原数组三、一维差分的应用【区间加】四、一维差分应用拓展【区间加等差单点查询】五、二维差分六、总结一、差分介绍与代码模板如果我们需要维护的数据是“两个相邻数据之差”，这就是差分。令diai−ai−1d_{i}a_{i}-a_…

文章目录

一、差分介绍与代码模板
二、从差分到原数组
三、一维差分的应用【区间加】
四、一维差分应用拓展【区间加等差+单点查询】
五、二维差分
六、总结

一、差分介绍与代码模板

如果我们需要维护的数据是“两个相邻数据之差”，这就是差分。令 $d_{i}=a_{i}-a_{i-1}$ ，则称 $d$ 是 $a$ 的差分数组。也可以写成 $Δai=ai−ai−1\Delta a_{i} = a_{i} - a_{i-1}$ 。

差分的写法与前缀和专栏的那篇介绍文章差不多，我们使用的数据数组 $a$ 和差分数组 $d$ 都是从1开始：

【差分模板】：

void getDiff(int a[], int n) { //a[0]=0, 使用[1,n]for (int i = 1; i <= n; ++i) d[i] = a[i] - a[i - 1]; //d[0]=0 
}

二、从差分到原数组

其实从前缀和也可以很轻易的求出原数组，不过是求区间和的区间的左右两端点相等罢了（即 $a [i] = s u m [i] - s u m [i - 1]$ ）。

同样的思想，我们也可以拿着差分数组 $d$ 推出 $a$ 数组。而且 $a [i] = a [i - 1] + d [i]$ 。 $a_{i}$ 相当于是差分数组 $d$ 的前缀和 $s u m [i]$ … 不说相当于，其实， $a$ 数组就是 $d$ 数组的前缀和数组。

如果要求 $a$ 数组的区间和，怎么做呢？(^_^)

所以，从我们约定的前缀和的写法(方便递推求前缀和数组)和求差分这两种角度来看，就写 $a [0] = 0$ 。

简单的举例：

a   : 0 | 3 7  5 8 (a[0]默认为0)
d   : 0 | 3 4 -2 3
sum : 0 | 3 7  5 8

很容易想明白，现在我在0楼，上了3楼，又上了4层楼，再往下走了两层楼，然后又上了三层楼，那么我现在位于0+3+4-2+3=8楼。

代码如下：

void getA(int p[], int n) { //d[0]=0, 使用[1,n]for (int i = 1; i <= n; ++i) a[i] = a[i - 1] + d[i];
}

前缀和可以让人以O(1)的时间求出一个区间的和。差分的用途也差不多，用来优化算法，甚至可以优化掉一个次方的复杂度。

下面具体介绍其应用。

三、一维差分的应用【区间加】

给定一个序列 $a$ ，其初值全为0，有很多(m)次操作，允许离线，形如： $\quad l \quad r \quad k$ ，将 $a_{[l,r]}$ 中的每个值加上 $k$ 。为方便，这里的 $\geq 1, r \geq 1$ 。最后输出整个数组，复杂度要求 $O (n)$ 。

举例如下：

a : 0 | 0 0 0 0 0 0A 1 2 3
-> a : 0 | 3 3 0 0 0 0A 2 5 -2
-> a : 0 | 3 1 -2 -2 -2 0A 5 6 3
-> a : 0 | 3 1 -2 -2 1 3

最简单的想法，就是对原数组进行操作，每次对区间 $[l, r]$ 进行相应的操作，时间为 $O (m n)$ ，m很大时甚至会达到平方的复杂度。下面的做法，可以真正做到 $O (n)$ 。

不难发现，区间 $[l, r]$ 加k，实际上发生了如下的两件事：

$a [l]$ 比前一个元素多了 $k$ ；
$a [r + 1]$ 比前一个元素少了 $k$ ；（不用大了小了的说法，会引起误解）

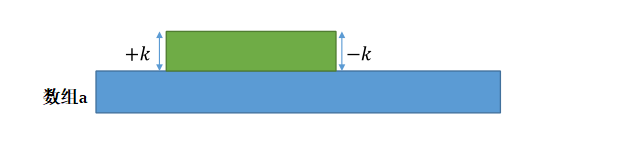
在差分数组 $d$ 的基础上面，可以对应转换为两个操作：

$d [l] + = k$ ；
$d [r + 1] - = k$ ；

即，一次区间加，只修改这两个元素，区间内部的数据之间的差值没有变化，对应于差分数组相应区别不变。

最后利用上面的（求前缀和）方法，从 $d$ 数组求出 $a$ 数组，即为答案。

例子：

a : 0 | 0 0 0 0 0 0
d : 0 | 0 0 0 0 0 0A 1 2 3
-> a : 0 | 3 3  0 0 0 0
-> d : 0 | 3 0 -3 0 0 0A 2 5 -2
-> a : 0 | 3  1 -2 -2 -2 0
-> d : 0 | 3 -2 -3  0  0 2A 5 6 3
-> a : 0 | 3  1 -2 -2  1 3
-> d : 0 | 3 -2 -3  0  3 2  (r + 1 > n, 计不计算都行, p数组开大一些)

区间加：

void add(int l, int r, int k) {d[l] += k;d[r + 1] -= k;
}void getA() {for (int i = 1; i <= n; ++i) //预先指定a[0]=0a[i] = a[i - 1] + d[i];

如果是单点加，用上面的add完全没问题：
$d_{x} += k, d_{x+1} -= k.$

本质和区间加一模一样。

四、一维差分应用拓展【区间加等差+单点查询】

给定一个序列 $a$ ，其初值全为0，有很多(m)次操作，操作有两种，强制在线，形如：

区间加等差数列： $\quad l \quad r \quad f \quad w$ ，将 $a_{[l,r]}$ 中的每个元素，加上首项为 $f$ 、公差为 $w$ 的等差数列对应的元素，即 $a_{[l]} += f_{1}$ ， $a_{[l + 1]} += f_{2}$ ，… 。
单点查询： $x$ ，求出 $a_{x}$ 。

为方便，这里的 $\geq 1, r \geq 1$ 。最后输出整个数组。

$e . g .$ 目前 $a=\{1,2,3,3,3,3\}$ ，给 $[3, 5]$ 加上首项为 $2$ 、公差为 $1$ 的等差数列， $a$ 变为 ${1,2,5,6,7,3\}$ 。

原来的 $d=\{1,1,1,0,0,0\}$ ，修改后的 $d$ 数组： ${1,1,3,1,1,-4\}$ 。显然： $a$ 区间加等差，相当于 $d$ 区间加常数、端点单点修改。

我们自然要把 $d_{[l + 1,r]}$ 加上 $w$ ， $d_{l}$ 加上 $f_{1}$ ；那么右端点呢？要把刚才的操作复原： $d_{r+1} -= f_{1} + (r - l)w$ 。

因此，我们要解决的问题在于，维护 $d$ 数组，支持单点修改、区间加，可以使用线段树或者差分+树状数组（比如 $d$ 的差分数组 $d' = \{1,0,0,-1,0,0\}$ ，修改后的 $d' = \{1, 0, 2, -2, 0, -5\}$ ，对 $a$ 加上等差数列，相当于对 $d$ 单点修改端点、区间加等差 $w$ ，相当于对 $d^{'}$ 单点修改端点、单点修改区间端点）加以解决。