您现在的位置是:主页 > news > 武汉手机网站建设信息/邹平县seo网页优化外包
武汉手机网站建设信息/邹平县seo网页优化外包
![]() admin2025/6/8 14:22:02【news】
admin2025/6/8 14:22:02【news】
简介武汉手机网站建设信息,邹平县seo网页优化外包,平面设计包括哪些方面,无锡网站建设价格费用关于第三章:第三章正式开始谈数据结构的实现,说的是最基本的链表、栈和队列。链表的用处非常多,以后的其他数据结构(比如散列表、图)也会用到,非常基本而实用的数据结构。而栈,则是编译器中递归实现的核心,…
关于第三章:
第三章正式开始谈数据结构的实现,说的是最基本的链表、栈和队列。
链表的用处非常多,以后的其他数据结构(比如散列表、图)也会用到,非常基本而实用的数据结构。
而栈,则是编译器中递归实现的核心,学习这个数据结构可以有效的帮助理解递归的工作原理。
至于队列,经常用在模拟一些比如顾客排队时间,进程时间调度的问题上。
笔记:
抽象数据类型(ADT,abstract data type):
ADT是一些操作的集合。抽象数据类型是数学的抽象;
在ADT的定义中根本没有涉及如何实现操作的集合,也不存在什么法则来告诉我们必须有那些操作,这是一个设计决策——由程序员从相应的需求中决定自己需要的操作,并将操作实现。
表ADT:
数据以
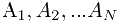 排列,将这类数据称为表,这个表的大小是N,大小为0的表称为空表。
排列,将这类数据称为表,这个表的大小是N,大小为0的表称为空表。
除空表外,我们说
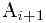 后继
后继
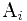 ,并称
,并称
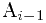 前驱
前驱
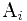 。我们不给
。我们不给
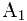 定义前驱,也不给
定义前驱,也不给
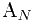 定义后继。
定义后继。
表的实现:
(1)数组实现:表的所有ADT都可以用数组实现,但是因为数组的连续储存方式,带来昂贵的插入和删除花费,所以我们一般不用简单数组作表的ADT实现。
(2)链表实现:由一些不在内存中相连的结构组成,每个结构包含指向下一结构的指针,称为Next指针。
头节点的使用:
因为处理
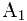 时遇到的边界处理问题,为了简化链表实现,我们给链表使用头节点。
时遇到的边界处理问题,为了简化链表实现,我们给链表使用头节点。
综上所述,一个带头节点的链表描述如下图:
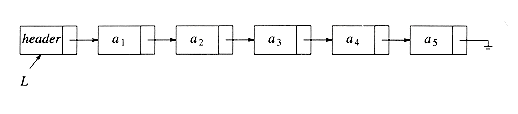
一个单链表的部分实现:
void Insert(List L,Position Prev,ElemType Input)
{
Position New;
New = CreateNode();
New->Data = Input;
New->Next = Prev->Next;
Prev->Next = New;
}
void Delete(List L,ElemType Search)
{
Position Prev;
Prev = FindPrev(L,Search);
if (Prev->Next != NULL) {
Position Target;
Target = Prev->Next;
Prev->Next = Target->Next;
free(Target);
}
}
Position Find(List L,ElemType Search)
{
Position Target;
Target = L->Next; // header assumed
while (Target != NULL &&
Target->Data != Search)
Target = Target->Next;
return Target;
}
Position FindPrev(List L,ElemType Search)
{
Position Prev;
Prev = L; // do not assumed header here!
while (Prev != NULL &&
Prev->Next->Data != Search)
Prev = Prev->Next;
return Prev;
}
注意对比Find()和FindPrev()函数对头节点的处理。
Find中,头节点内的无效元素会影响查找结果,所有在这里把头节点忽略掉。
而在FindPrev中,头节点可能作为某节点的前驱节点(比如查找目标是第一个有效节点的时候),所以在这里不忽略头节点。
List DeleteList(List L)
{
if (L->Next != NULL) {
Position Target,Temp;
Target = L->Next;
L->Next = NULL;
while (Target != NULL) {
Temp = Target->Next;
free(Target);
Target = Temp; // notice!
}
}
return L;
}
另外,编写DeleteList函数时,也要注意节点的处理,否则删除将不能正确进行。
双链表、循环链表:


这两个链表的实现和单链表类似,只是节点的结构不同。
另外,要注意的是边界节点的处理,这里就不展开谈了。
struct db_list {
ElemType Data;
Pos Prev;
Pos Next;
};
游标(数组式链表)的实现:
游标是在不支持指针的语言中,使用链表的方法,它使用数组来模拟链表的运行,包括创建节点和删除节点。
void InitCursor(void)
{
int i;
for (i = 0; i < SpaceSize; i++)
Cursor[i].Next = i+1;
Cursor[i - 1].Next = 0;
}
List CreateList(void)
{
Position Header;
Header = Alloc();
Cursor[Header].Next = 0;
return Header;
}
首先,要初始化数组,制造首尾相连的效果。
然后,再编写两个函数实现数组中类似Alloc和Free的功能。
Position Alloc(void)
{
Position P;
P = Cursor[0].Next;
Cursor[0].Next = Cursor[P].Next;
return P;
}
void Free(Position P)
{
Cursor[0].Next = Cursor[P].Next;
Cursor[0].Next = P;
}
游标的各种操作和链表原理相同,要注意的是,在游标中的赋值,比如,注意不要这样:
P = P->Next
而是
P = Cursor[L].Next;
栈ADT:
栈是限制删除和插入只能在一个位置上进行的表,该位置叫做栈的顶。
栈又叫LIFO(后进现出,last in first out)表。
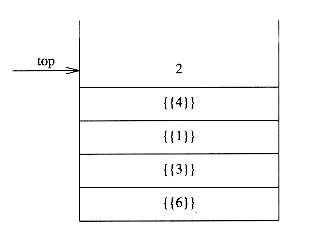
栈的数组实现:
栈的数组实现比链表实现典型,这里只贴数组实现代码。
struct StackRecord {
int Size;
int Position;
ElemType * Data;
};
void Push(Stack S,ElemType Input)
{
if (!IsFull(S)) {
S->Data[++S->Position] = Input;
}
}
void Pop(Stack S)
{
if (!IsEmpty(S)) {
S->Position--;
}
}
注意Push中的
S->Data[++S->Position] = Input;
++一定要前置。
栈实现递归:
值得一提的是,在程序语言用,递归是使用栈实现的。
在下面的一段尾递归代码:
void Res(int num)
{
if (num == 0){
return;
}
else {
printf("%d\n",num);
Res(--num);
}
}
如果我们把5赋值给函数RecuresNum运行,则它的展开模型是这样的:
puts(5);
Res(4);
| |
|--puts(4); |
|--Res(3);
| |
|--puts(3); |
|--Res(2);
| |
|--puts(2); |
|--Res(1);
| |
|--puts(1); |
|--Res(0); |
| |
|------->----------|
(不会用linux下的画图软件,原谅我XD)
其中每个Res调用,都会将前一个Res函数的数据通过栈Push保存起来,等到新函数调用完毕,就原路通过Pop返回到原来的函数上。
队列ADT:
队列是插入在一端进行,而删除在另一端进行的表。
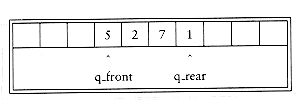
同样的,队列的链表实现也相当直观,我们在这里只贴数组实现的代码。
struct QueueRecord {
int Capacity;
int Size;
Pos Front;
Pos Rear;
ElemType * Data;
};
void Enqueue(Queue Q,ElemType Input)
{
if (!IsFull(Q)) {
++Q->Size;
Q->Rear = Succ(Q,Q->Rear);
Q->Data[Q->Rear] = Input;
}
else {
fprintf(stderr,"Enqueue fail!");
}
}
void Dequeue(Queue Q)
{
if (!IsEmpty(Q)) {
--Q->Size;
Q->Front = Succ(Q,Q->Front);
}
else {
fprintf(stderr,"Dequeue fail!");
}
}
static Pos Succ(Queue Q,Pos Index)
{
if (++Index == Q->Capacity)
Index = 0;
return Index;
}
值得注意的是回绕的处理,其他的操作都很简单。
习题答案:
3.3 (a)
void SwapWithNext( Position BeforeP, List L )
{
Position P, AfterP;
P = BeforeP->Next;
AfterP = P->Next; /* Both P and AfterP assumed not NULL. */
P->Next = AfterP->Next;
BeforeP->Next = AfterP;
AfterP->Next = P;
}
3.4 链表实现交操作
List
Intersect( List L1, List L2 )
{
List Result;
Position L1Pos, L2Pos, ResultPos;
L1Pos = First( L1 ); L2Pos = First( L2 );
Result = MakeEmpty( NULL );
ResultPos = First( Result );
while( L1Pos != NULL && L2Pos != NULL )
{
if( L1Pos->Element < L2Pos->Element )
L1Pos = Next( L1Pos, L1 );
else if( L1Pos->Element > L2Pos->Element )
L2Pos = Next( L2Pos, L2 );
else
{
Insert( L1Pos->Element, Result, ResultPos );
L1 = Next( L1Pos, L1 ); L2 = Next( L2Pos, L2 );
ResultPos = Next( ResultPos, Result );
}
}
return Result;
}
3.5 链表实现并操作
List
Union( List L1, List L2 )
{
List Result;
ElementType InsertElement;
Position L1Pos, L2Pos, ResultPos;
L1Pos = First( L1 ); L2Pos = First( L2 );
Result = MakeEmpty( NULL );
ResultPos = First( Result );
while ( L1Pos != NULL && L2Pos != NULL ) {
if( L1Pos->Element < L2Pos->Element ) {
InsertElement = L1Pos->Element;
L1Pos = Next( L1Pos, L1 );
}
else if( L1Pos->Element > L2Pos->Element ) {
InsertElement = L2Pos->Element;
L2Pos = Next( L2Pos, L2 );
}
else {
InsertElement = L1Pos->Element;
L1Pos = Next( L1Pos, L1 ); L2Pos = Next( L2Pos, L2 );
}
Insert( InsertElement, Result, ResultPos );
ResultPos = Next( ResultPos, Result );
}
/* Flush out remaining list */
while( L1Pos != NULL ) {
Insert( L1Pos->Element, Result, ResultPos );
L1Pos = Next( L1Pos, L1 ); ResultPos = Next( ResultPos, Result );
}
while( L2Pos != NULL ) {
Insert( L2Pos->Element, Result, ResultPos );
L2Pos = Next( L2Pos, L2 ); ResultPos = Next( ResultPos, Result );
}
return Result;
}
注意3。4和3。5的区别。
3。12 不用递归翻转单链表
List
ReverseList( List L )
{
Position CurrentPos, NextPos, PreviousPos;
PreviousPos = NULL;
CurrentPos = L;
NextPos = L->Next;
while( NextPos != NULL )
{
CurrentPos->Next = PreviousPos;
PreviousPos = CurrentPos;
CurrentPos = NextPos;
NextPos = NextPos->Next;
}
CurrentPos->Next = PreviousPos;
return CurrentPos;
}
3。15 自调整表的链表实现
Position
Find( ElementType X, List L )
{
Position PrevPos, XPos;
PrevPos = FindPrevious( X, L );
if( PrevPos->Next != NULL ) /* Found. */
{
XPos = PrevPos ->Next;
PrevPos->Next = XPos->Next;
XPos->Next = L->Next;
L->Next = XPos;
return XPos;
}
else
return NULL;
}
3。24
因为只有49个活动记录,栈空间不会用完。但因为计算是指数上升的,所以计算不会在合理的时间内返回结果。








