有穷自动机的非形式化定义
非形式化定义,即非数学语言的定义。
自动机是一种抽象的机器,它有很多个状态,用圆圈来表示。状态与状态之间有箭头,箭头上有所需要的条件,
也即只有满足箭头上的条件时才能从一个状态走到另一个状态。状态的目的是记住系统历史的有关部分,也即记住所
输入的字符串都满足了自动机系统的哪些条件,这就是所说的记住历史。而有穷就是说这个自动机的状态是有限的,
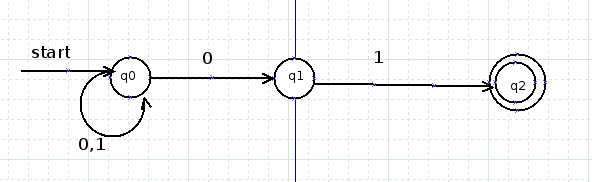
这样才能够编程来实现它。下面是一个简单的有穷自动机,它扫描所给的字符串,判断其中是否包含字符串then。

有穷自动机的形式化定义
有穷自动机分为:①确定型有穷自动机②非确定型有穷自动机
有穷自动机确定与否,只在于他们转移函数的定义不同。
记状态机$A$为 $$A = ( V,\sum,\delta,V_{N},V_{T} )$$
确定型有穷自动机(Deterministic Finite Automaton)的定义:
1.一个有穷的状态集合,通常记作V。状态非为非终结状态$V_{N}$和终结状态$V_{T}$
2.一个有穷的输入符号字母表。通常记作$\sum$。
3.一个转移函数,该转移函数以一个状态和一个输入符号作为变量,返回一个状态。通常记做$\delta$。
如果从状态p到状态q有一条权值为a的箭头,那么$\delta(p,a)=q$
基础:$\delta(p,\epsilon)=p$ ,也就是说,如果在状态p下不读入输入,就还处于状态p。
归纳:假设w是形如xa的串,a是w的结尾符号,x是除结尾符号外所有的符号的串,那么有$\delta(p,w)=\delta(\delta(p,x),a)$
也就是说为了计算$\delta(p,w)$,必须先计算$\delta(p,x) = q$, 然后再计算$\delta(q,a)$
也即$\delta(p,w) = \delta(q,a)$
其实上面就是一个递归的定义。
4.一个初始化状态,也即入口。通常记作$S$,$S \in V_{N}$
5.一个终结状态的集合$V_{T}$。
非确定型有穷自动机(Nondeterministic Finite Automaton)的定义:
1.一个有穷的状态集合,通常记作V。状态非为非终结状态$V_{N}$和终结状态$V_{T}$
2.一个有穷的输入符号字母表。通常记作$\sum$。
3.一个转移函数,该转移函数以一个状态和一个输入符号作为变量,返回的状态的个数不再是一个,而有可能是多个。
基础:$\delta(p,\epsilon)=p$ ,也就是说,如果在状态p下不读入输入,就还处于状态p。
归纳:假设w是形如xa的串,a是w的结尾符号,x是除结尾符号外所有的符号的串,
假设$\delta(p,x)={p_1,p_2,..,p_k}$,即这个函数有k个值。
设$\bigcup_{i=1}^{k}\delta(p_{i},a) = \{r_1,r_2,...,r_m\}$
那么有$\delta(p,w) = \{r_1,r_2,...,r_m\}$。即要计算$\delta(p,w)$,那么先计算$\delta(p,x)$,然后从这些状态出发,进行带a标记的箭头的转移。
4.一个初始化状态,也即入口。通常记作$S$,$S \in V_{N}$
5.一个终结状态的集合$V_{T}$。
DFA与NFA的对比
DFA的好处是状态转移的函数是确定的,即能知道下一个状态如何走。
而NFA如果状态转移函数是多值的,那么将面临输入符号而不知道如何走的情况。
但是NFA通常比DFA更容易设计。
考虑下面这种情况,要设计一个有穷自动机,它的任务是接受所有的仅以01结尾的0和1的串。
那么很容易想到下面的这个NFA