前言

若想学习Markdown，请参见我的其他博客：Markdown详细教程+技巧总结 。
若想学习LaTeX，请参见我的其他博客：LaTeX详细教程+技巧总结 。

若使用LaTeX编译器编写LaTeX数学公式，需要在导言区引用数学公式的宏包，代码为\usepackage{amsmath}；若要修改公式的字体，还需要引用宏包\usepackage{amsfonts}。

若使用Markdown编写LaTeX数学公式，CSDN支持LaTeX数学公式，但有些本地编辑器可能不支持LaTeX数学公式，Typroa可以更改设置支持，VS Code可以通过安装扩展的方式支持。

本篇博客内容包含前言，注意事项，插入公式，注释，编号，转义字符，换行与对齐，字体，空格，上下标，括号，大括号和行标，分式，开方，对数，省略号，最值，方程组和分段函数，累加和累乘，矢量，积分，极限，导数与偏导，矩阵，表格，希腊字母，运算符，黑板粗体（空心字母），戴帽符号，特殊符号，等等。

1. 官方文档（英文）：
   传送门：官方文档
   网址：http://www.ctex.org/documents/packages/math/index.htm
2. 中文文档：
   传送门：中文教程
   网址：https://www.latexlive.com/help
3. 技巧：使用在线LaTeX公式编辑器，来生成LaTeX公式代码，然后复制到LaTeX编辑器（或Markdown编辑器）中，并在两边加上$或$$即可。
   在线LaTeX公式编辑器网址：https://www.latexlive.com/
4. 插入公式
   左对齐公式（行中公式）：$数学公式$
   居中公式（独立公式）：$$数学公式$$
   注意：使用$行中公式时，数学公式与$连接处不要有空格，否则公式不会显示；使用$$居中公式时，数学公式与$$连接处可以有空格。即$ 数学公式 $ 不显示公式。
5. 注释：%为单行注释。
6. 细节请参照下文。

注意事项

1. 使用$，即行中公式时，数学公式与$连接处不要有空格，否则公式不会显示。即$ 数学公式 $ 不显示公式。
2. 使用$$，即居中公式时，数学公式与$$连接处可以有空格。
3. 使用$$时，上方要空一行。
4. =不要单独打一行，否则可能会出错。
5. + - * / = ( ) | , . '等符号直接在$或$$之间输入即可识别。

插入公式

左对齐公式（行中公式）：$数学公式$
居中公式（独立公式）：$$数学公式$$

注意： 注意事项请参照目录章节中的注意事项子章节。

左对齐例子：$x+y=z$
$x+y=z$

居中对齐例子：$$x+y=z$$
$$x+y=z$$

注释

%为单行注释。

例子：

$$
%第一个极限
\lim_{n \to +\infty} \frac{1}{n(n+1)}
\quad %空一格
and %英文单词and
\quad %空一格
%第2个极限
\lim_{x\leftarrow{example} \infty} \frac{1}{n(n+1)}
$$

显示：
$$\underset{n\to +\infty }{\lim }\frac{1}{n(n+1)}and\underset{x\leftarrow example\infty }{\lim }\frac{1}{n(n+1)}$$

编号

Markdown编辑器

在公式末尾使用\tag{编号}来实现公式手动编号，大括号内的内容可以自定义。

例子：

$$
x+y=z
\tag{1}
$$

显示：
$$x+y=z\text{\hspace{1em}(1)}$$

LaTeX编辑器

包含自动编号和手动编号两种方式。
详情请参见我的另一篇博客LaTeX详细教程中的公式编号章节。
此处简单介绍使用方法。

自动编号
使用\begin{equation}和\end{equation}进行公式输入，要同时使用，且编号不能够修改。

例子：

\begin{equation}
a^2+b^2=c^2
\end{equation}

显示：

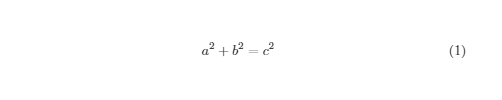
手动编号
在公式末尾使用\tag{编号}来实现公式手动编号，大括号内的内容可以自定义。需要使用\usepackage{amsmath}宏包，不能写在$或$$中，会报错。

例子：

\begin{equation}
a^2+b^2=c^2
\tag{2}
\end{equation}

显示：

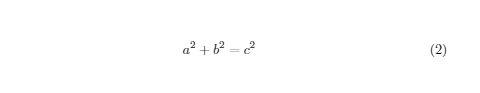
转义字符

在公式中输入_或^等符号时，会产生上下标功能，若想输入符号本身则需要转义字符\，写法为\+字符，示例如下：

例子：

$$
% \ 为转义字符
home\_name=honor
$$

显示：
$$home\_name=honor$$

换行与对齐

换行

使用\\进行换行，最后一行的\\可写可不写。

例子：

$$
f(x)=2x+1 \\
=2+1 \\
=3
$$

显示：
$$\begin{gathered} f(x)=2x+1 \\ =2+1 \\ =3 \end{gathered}$$

对齐

使用\begin{aligned}进行对齐，&表示对齐位置，一般都在=前面。

例子：

\begin{aligned}
f(x)&=2x+1 \\
&=2+1 \\
&=3
\end{aligned}

显示：

$$\begin{array}{rl}f(x)& =2x+1\\ & =2+1\\ & =3\end{array}$$

字体

若要对公式的某一部分字符进行字体转换，可以用 \字体{需转换的字符} 命令，其中 \字体 部分可以参照下表选择合适的字体。一般情况下，公式默认为意大利体，直体为罗马体 \rm。一般里面一层大括号可省略。

注意：在LaTeX编辑器中，修改公式字体时，需要引入宏包\usepackage{amsmath}和\usepackage{amsfonts}，且在公式中输入。

输入	说明	显示
\mathit 或 \it	斜体（默认，意大利体）	$D$
\mathrm 或 \rm	罗马体	$\mathrm{D}$
\mathbf 或 \bf	粗体	$\mathbf{D}$
\mathbb	黑板粗体	$\mathbb{D}$
\mathsf 或 \sf	等线体	$\mathsf{D}$
\mathcal	花体	$\mathcal{D}$
\mathscr	手写体	$\mathcal{D}$
\mathtt	打字机体	$\mathtt{D}$
\mathfrak	哥特体	$\mathfrak{D}$
\boldsymbol	黑体	$\mathbf{D}$

例子：
$$A+\mathbb{BC}+D$$

显示：
$$A+\mathbb{B}\mathbb{C}+D$$

空格

\quad：空一格
\qquad：空两格

例子：
$$x \quad y \qquad z$$

显示：
$$xyz$$

上下标

^表示上标， _ 表示下标。如果上下标的内容多于一个字符，需要用 {}将这些内容括成一个整体。上下标可以嵌套，也可以同时使用。

例子：
$$x^{y^z_w}=(1+{\rm e}^x)^{-2xy^w}$$

显示：
$$x^{y_w^z}=(1+{\mathrm{e}}^x{)}^{-2x{y}^w}$$

上下标同时使用例子：
$$f(x) = x_1^2 + {x}_{2}^{2}$$

显示：
$$f(x)=x_1^2+x_2^2$$

括号

()、[]、|表示符号本身，使用 \{\} 来表示 {}。当要显示大号的括号或分隔符时，要用 \left 和 \right 命令，如$\left(表达式\right)$，大号的括号详见下一节）。

一些特殊的括号：

特殊括号	输入	显示
尖括号	$\langle表达式\rangle$	$⟨表达式⟩$
向上取整	$\lceil表达式\rceil$	$\lceil 表达式\rceil$
向下取整	$\lfloor表达式\rfloor$	$\lfloor 表达式\rfloor$
大括号	$\lbrace表达式\rbrace$	{表达式}\lbrace表达式\rbrace{表达式}

例子：
$$f(x,y,z) = 3y^2z \left( 3+\frac{7x+5}{1+y^2} \right)$$

显示：
$$f(x,y,z)=3y^{2}z\left(3+\frac{7x+5}{1+y^2}\right)$$

大括号

方法1
使用 \left和 \right来创建自动匹配高度的括号，包含 (圆括号)、[方括号]、|绝对值|。

例子：

$$
f\left(\left[\frac{1+\left\{x,y\right\}}{\left(\frac{x}{y}+\frac{y}{x}\right)\left(u+1\right)}+a\right]^{3/2}
\right)
$$

显示：
f([1+{x,y}(xy+yx)(u+1)+a]3/2)f\left( \left[ \frac{ 1+\left\{x,y\right\} }{ \left( \frac{x}{y}+\frac{y}{x} \right) \left(u+1\right) }+a \right]^{3/2} \right) f⎝⎜⎛​⎣⎡​(yx​+xy​)(u+1)1+{x,y}​+a⎦⎤​3/2⎠⎟⎞​

有时候要用\left.或\right.进行匹配而不显示本身。

例子：
$$\left. \frac{ {\rm d}u}{ {\rm d}x} \right| _{x=0}$$

显示：
$${\frac{\mathrm{d}u}{\mathrm{d}x}|}_{x=0}$$

方法2
使用\big和\bigg来创建逐级变大的括号，包含 (圆括号)、[方括号]、|绝对值|。

例子：

$$\bigg( \big( ( ) \big) \bigg)$$
$$\bigg[ \big[ [ ] \big] \bigg]$$
$$\bigg| \big| | | \big| \bigg|$$

显示：
$$\left(\right(()\left)\right)$$
$$\left[\right[[]\left]\right]$$
$$\left|\right|||\left|\right|$$

分式

通常使用 \frac {分子} {分母} 命令产生一个分式，分式可嵌套。
便捷情况可直接输入 \frac ab来快速生成一个 $\frac{a}{b}$。
如果分式很复杂，亦可使用 分子 \over 分母 命令，此时分式仅有一层。

例子：
$$\frac{a-1}{b-1} \quad and \quad {a+1\over b+1}$$

显示：
$$\frac{a-1}{b-1}and\frac{a+1}{b+1}$$

根式

\sqrt [根指数] {被开方数}

注意：缺省根指数时为2

例子：
$$\sqrt{2} \quad and \quad \sqrt[n]{x+y}$$

显示：
$$\sqrt{2}and\sqrt[n]{x+y}$$

对数

\log_{对数底数}{表达式}

表达式的大括号可省略

显示：
${\log }_{x+y}(z+1)$

省略号

数学公式中常见的省略号有两种，\ldots 表示与文本底线对齐的横向省略号 $\dots$，\cdots 表示与文本中线对齐的横向省略号 $\cdots$，\vdots表示纵向省略号 $⋮$，\ddots表示斜向省略号 $\ddots$。

例子：
$$f(x_1,x_2,\underbrace{\ldots}_{\rm ldots} ,x_n) = x_1^2 + x_2^2 + \underbrace{\cdots}_{\rm cdots} + x_n^2$$

显示：
$$f(x_1,x_2,\underset{\mathrm{l}\mathrm{d}\mathrm{o}\mathrm{t}\mathrm{s}}{\underbrace{\dots }},x_n)=x_1^2+x_2^2+\underset{\mathrm{c}\mathrm{d}\mathrm{o}\mathrm{t}\mathrm{s}}{\underbrace{\cdots }}+x_n^2$$

最值

\max_{下标表达式}{最值表达式}表示最大值，\min_{下标表达式}{最值表达式}表达最小值。
例子：
$$||x||_\infty=\max_{1\leq i\leq n}{|x_i|}$$

显示：
$$||x|{|}_{\infty }=\underset{1\le i\le n}{\max }|x_i|$$

方程组和分段函数

方程组

方程组有2种方式，分别是\begin{aligned}和\begin{cases}方式，&表示对齐位置，推荐使用\begin{cases}方式，使用方法如下：

\begin{aligned}方式：可以使方程组根据=对齐

$$
\left\{
\begin{aligned}
a+b&=2 \\
a-b&=4 \\
\end{aligned}
\right.
$$

显示：
$$\{\begin{array}{rl}a+b& =2\\ a-b& =4\end{array}$$

\begin{cases}方式（推荐）：简便，但无法根据=对齐

$$
\begin{cases}
a+b=2 \\
a-b=4 \\
\end{cases}
$$

显示：
$$\{\begin{array}{l}a+b=2\\ a-b=4\end{array}$$

分段函数

分段函数可以通过\begin{cases}方式实现，不同的是方程式和条件之间要用&符号隔开。

例子：

$$
y =
\begin{cases}
\sin(x)       & x<0 \\
x^2 + 2x +4   & 0 \leq x < 1 \\
x^3           & x \geq 1 \\
\end{cases}
$$

显示：
$$y=\{\begin{array}{ll}\sin (x)& x<0\\ x^2+2x+4& 0\le x<1\\ x^3& x\ge 1\end{array}$$

累加和累乘

使用 \sum_{下标表达式}^{上标表达式}{累加表达式}来输入一个累加。
与之类似，使用 \prod \bigcup \bigcap来分别输入累乘、并集和交集。
此类符号在行内显示时上下标表达式将会移至右上角和右下角。

例子：
$$\sum_{i=1}^n \frac{1}{i^2} \quad and \quad \prod_{i=1}^n \frac{1}{i^2} \quad and \quad \bigcup_{i=1}^{2} R$$

显示：
$$\sum _{i=1}^n\frac{1}{i^2}and\prod _{i=1}^n\frac{1}{i^2}and\bigcup _{i=1}^{2}R$$

矢量

使用 \vec{矢量}来自动产生一个矢量。
也可以使用 \overrightarrow等命令自定义字母上方的符号。

例子：
$$\vec{a} \cdot \vec{b}=0\$$

显示：
$$\vec{a}\cdot \vec{b}=0$$

例子：
$$\overleftarrow{xy} \quad and \quad \overleftrightarrow{xy} \quad and \quad \overrightarrow{xy}$$

显示：
$$\overleftarrow{xy}and\overleftrightarrow{xy}and\overrightarrow{xy}$$

极限

\lim_{变量 \to 表达式} 表达式
如有需求，可以更改 \to 符号至任意符号。

例子：
$$\lim_{n \to +\infty} \frac{1}{n(n+1)} \quad and \quad \lim_{x\leftarrow{example} \infty} \frac{1}{n(n+1)}$$

显示：
$$\underset{n\to +\infty }{\lim }\frac{1}{n(n+1)}and\underset{x\leftarrow example\infty }{\lim }\frac{1}{n(n+1)}$$

导数

导数
${\rm d}x$或${\text d}x$或$\text{d}x$

$\mathrm{d}x$或$\text{d}x$或$\text{d}x$

偏导
$\frac{\partial y}{\partial x}$

$\frac{\partial y}{\partial x}$

梯度
$\nabla f(x)$

$\nabla f(x)$

积分

\int_积分下限^积分上限 {被积表达式}

例子：
$$\int_0^1 {x^2} \,{\rm d}x$$

显示：
$${\int }_0^1{x}^2\mathrm{d}x$$

矩阵

基础矩阵

使用\begin{matrix}…\end{matrix} 这样的形式来表示矩阵，在\begin 与\end 之间加入矩阵中的元素即可。矩阵的行之间使用\\ 分隔，\\表示换行，列之间使用& 分隔，&表示对齐位置。

例子：

$$
\begin{matrix}
1 & x & x^2 \\
1 & y & y^2 \\
1 & z & z^2 \\
\end{matrix}
$$

显示：
$$\begin{array}{ccc}1& x& x^2\\ 1& y& y^2\\ 1& z& z^2\end{array}$$

带括号的矩阵

使用\left 与\right 表示括号

如果要对矩阵加括号，可以像上文中提到的一样，使用\left 与\right 配合表示括号符号。

例子：

$$
\left[
\begin{matrix}
1 & x & x^2 \\
1 & y & y^2 \\
1 & z & z^2 \\
\end{matrix}
\right]
$$

显示：
$$\left[\begin{array}{ccc}1& x& x^2\\ 1& y& y^2\\ 1& z& z^2\end{array}\right]$$

使用特殊的matrix

带括号的矩阵也可以使用特殊的matrix 。即替换\begin{matrix}…\end{matrix} 中matrix 为pmatrix ，bmatrix ，Bmatrix ，vmatrix , Vmatrix 。

1. pmatrix：$\begin{pmatrix}1 & 2 \\ 3 & 4\\ \end{pmatrix}$
   $\left(\begin{array}{cc}1& 2\\ 3& 4\end{array}\right)$
2. bmatrix：$\begin{bmatrix}1 & 2 \\ 3 & 4\\ \end{bmatrix}$
   $\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]$
3. Bmatrix：$\begin{Bmatrix}1 & 2 \\ 3 & 4\\ \end{Bmatrix}$
   $\left\{\begin{array}{cc}1& 2\\ 3& 4\end{array}\right\}$
4. vmatrix：$\begin{vmatrix}1 & 2 \\ 3 & 4\\ \end{vmatrix}$
   $\left|\begin{array}{cc}1& 2\\ 3& 4\end{array}\right|$
5. Vmatrix：$\begin{Vmatrix}1 & 2 \\ 3 & 4\\ \end{Vmatrix}$
   $\Vert \begin{array}{cc}1& 2\\ 3& 4\end{array}\Vert$

行列式

方法已经在上一节带括号的矩阵中有所介绍，此处只写一个例子。

例子1：使用\left 与\right 表示括号

$$
\left|
\begin{matrix}
1 & x & x^2 \\
1 & y & y^2 \\
1 & z & z^2 \\
\end{matrix}
\right|
$$

显示：
$$\left|\begin{array}{ccc}1& x& x^2\\ 1& y& y^2\\ 1& z& z^2\end{array}\right|$$

例子2：使用特殊的matrix

$$
\begin{vmatrix}
1 & x & x^2 \\
1 & y & y^2 \\
1 & z & z^2 \\
\end{vmatrix}
$$

显示：
$$\left|\begin{array}{ccc}1& x& x^2\\ 1& y& y^2\\ 1& z& z^2\end{array}\right|$$

元素省略的矩阵

可以使用\cdots ：$\cdots$，\ddots：$\ddots$ ，\vdots：$⋮$ ，来省略矩阵中的元素。

例子：

$$
\begin{pmatrix}
1&a_1&a_1^2&\cdots&a_1^n\\
1&a_2&a_2^2&\cdots&a_2^n\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
1&a_m&a_m^2&\cdots&a_m^n\\
\end{pmatrix}
$$

显示：
$$\left(\begin{array}{ccccc}1& a_1& a_1^2& \cdots & a_1^n\\ 1& a_2& a_2^2& \cdots & a_2^n\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& a_m& a_m^2& \cdots & a_m^n\end{array}\right)$$

增广矩阵

增广矩阵需要使用前面的表格中使用到的\begin{array} ... \end{array} 来实现。

例子：

$$
\left[  \begin{array}  {c c | c} %这里的c表示数组中元素对其方式：c居中、r右对齐、l左对齐，竖线表示2、3列间插入竖线
1 & 2 & 3 \\
\hline %插入横线，如果去掉\hline就是增广矩阵
4 & 5 & 6
\end{array}  \right]
$$

显示：
$$\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\end{array}\right]$$

表格

使用\begin{array}{列样式}…\end{array} 这样的形式来创建表格，列样式可以是clr 表示居中，左，右对齐，还可以使用| 表示一条竖线。表格中各行使用\\ 分隔，各列使用& 分隔。使用\hline 在本行前加入一条直线。

例子：

$$
\begin{array}{c|lcr}
n & \text{Left} & \text{Center} & \text{Right} \\
\hline
1 & 0.24 & 1 & 125 \\
2 & -1 & 189 & -8 \\
3 & -20 & 2000 & 1+10i \\
\end{array}
$$

显示：
$$\begin{array}{clcr}n& \text{Left}& \text{Center}& \text{Right}\\ 1& 0.24& 1& 125\\ 2& -1& 189& -8\\ 3& -20& 2000& 1+10i\end{array}$$

希腊字母

输入 \小写希腊字母英文全称和\首字母大写希腊字母英文全称来分别输入小写和大写希腊字母。
对于大写希腊字母与现有字母相同的，直接输入大写字母即可。

输入	显示	输入	显示
$\alpha$	$\alpha$	$A$	$A$
$\beta$	$\beta$	$B$	$B$
$\gamma$	$\gamma$	$\Gamma$	$\Gamma$
$\delta$	$\delta$	$\Delta$	$\Delta$
$\epsilon$	$ϵ$	$E$	$E$
$\zeta$	$\zeta$	$Z$	$Z$
$\eta$	$\eta$	$H$	$H$
$\theta$	$\theta$	$\Theta$	$\Theta$
$\iota$	$\iota$	$I$	$I$
$\kappa$	$\kappa$	$K$	$K$
$\lambda$	$\lambda$	$\Lambda$	$\Lambda$
$\nu$	$\nu$	$N$	$N$
$\mu$	$\mu$	$M$	$M$
$\xi$	$\xi$	$\Xi$	$\Xi$
$o$	$o$	$O$	$O$
$\pi$	$\pi$	$\Pi$	$\Pi$
$\rho$	$\rho$	$P$	$P$
$\sigma$	$\sigma$	$\Sigma$	$\Sigma$
$\tau$	$\tau$	$T$	$T$
$\upsilon$	$\upsilon$	$\Upsilon$	${\rm Y}$
$\phi$	$\varphi$	$\Phi$	$\Phi$
$\chi$	$\chi$	$X$	$X$
$\psi$	$\psi$	$\Psi$	$\Psi$
$\omega$	$\omega$	$\Omega$	$\Omega$

黑板粗体（空心字母）

空心字母属于一种字体，官方名称为黑板粗体，仅对大写字母起作用。若使用LaTeX编辑器，使用前需要在导言区引入宏包\usepackage{amsfonts}，并在公式中修改字体。

使用$\mathbb{字母}$即可使用空心字母，下方示例仅展示3个字母（M，R，L），其它字母同理。

大写字母	公式语言
$\mathbb{M}$	$\mathbb{M}$
$\mathbb{R}$	$\mathbb{R}$
$\mathbb{L}$	$\mathbb{L}$
…	…

运算符

对于加减除，对应键盘上便可打出来，但是对于乘法，键盘上没有这个符号，所以我们应该输入 \times 来显示一个 $\times$ 号。

普通字符在数学公式中含义一样，除了 # $ % & ~ _ { } 若要在数学环境中表示这些符号# $ % & _ { }，需要分别表示为\# \$ \% \& \_ \{ \}，即在个字符前加上转义字符 \ 。

关系运算符

关系运算符	公式语言	集合运算符	公式语言	对数运算符	公式语言
$\pm$	$\pm$	$\varnothing$	$\emptyset$	$\log$	$\log$
$\times$	$\times$	$\in$	$\in$	$\lg$	$\lg$
$÷$	$\div$	$\notin$	$\notin$	$\ln$	$\ln$
$\mid$	$\mid$	$\subset$	$\subset$
$\nmid$	$\nmid$	$\supset$	$\supset$
$\cdot$	$\cdot$	$\subseteq$	$\subseteq$
$\circ$	$\circ$	$\supseteq$	$\supseteq$
$\ast$	$\ast$	$\cap$	$\cap$(可加前缀big)
$\odot$	$\odot$(可加前缀big)	$\cup$	$\cup$(可加前缀big)
$\otimes$	$\otimes$(可加前缀big)	$\vee$	$\vee$(可加前缀big)
$\oplus$	$\oplus$(可加前缀big)
$\le$	$\leq$ 或 $\le$	$\wedge$	$\wedge$(可加前缀big)
$\ge$	$\geq$ 或 $\ge$	$\uplus$	$\uplus$(可加前缀big)
$\ne$	$\neq$ 或 $\ne$	$\bigsqcup$	$\sqcup$(可加前缀big)
$\sim$	$\sim$
$\backsim$	$\backsim$
$\simeq$	$\simeq$
$\cong$	$\cong$
$\approx$	$\approx$
$\equiv$	$\equiv$
$\ll$	$\ll$
$\gg$	$\gg$
$\sum$	$\sum$
$\prod$	$\prod$
$\coprod$	$\coprod$
$\prec$	$\prec$
$⪯$	$\preceq$
$\succ$	$\succ$
$⪰$	$\succeq$
$+,-,\ast ,/,<,>,=$	$+, -, *, /, <, >, =$

其中，部分公式添加前缀big可以放大，删掉big前缀即为正常大小。
例如，$\odot$为$\odot$，$\bigodot$为$⨀$。

三角运算符

三角运算符	公式语言	微积分运算符	公式语言	逻辑运算符	公式语言
$\perp$	$\bot$	$\prime$	$\prime$	$\because$	$\because$
$\angle$	$\angle$	$\int$	$\int$	$\therefore$	$\therefore$
$30^{\circ }$	$30^\circ$	$\iint$	$\iint$	$\forall$	$\forall$
$\sin$	$\sin$	$\iiint$	$\iiint$	$\exists$	$\exists$
$\cos$	$\cos$	$\oint$	$\oint$	$\ne$	$\not=$
$\tan$	$\tan$	$\lim$	$\lim$	$\ngtr$	$\not>$
$\cot$	$\cot$	$\infty$	$\infty$	$\not\subset$	$\not\subset$
$\sec$	$\sec$	$\nabla$	$\nabla$	$\neg$	$\neg$
$\csc$	$\csc$
$△$	$\bigtriangleup$
$▽$	$\bigtriangledown$
$◃$	$\triangleleft$
$▹$	$\triangleright$

箭头运算符

箭头符号	公式语言
$\uparrow$	$\uparrow$
$\downarrow$	$\downarrow$
$\updownarrow$	$\updownarrow$
$\Uparrow$	$\Uparrow$
$\Downarrow$	$\Downarrow$
$\Updownarrow$	$\Updownarrow$
$\to$	$\rightarrow$ 或 $\to$
$\leftarrow$	$\leftarrow$ 或 $\gets$
$\leftrightarrow$	$\leftrightarrow$
$\Rightarrow$	$\Rightarrow$
$\Leftarrow$	$\Leftarrow$
$\iff$	$\Leftrightarrow$
$⟶$	$\longrightarrow$
$⟵$	$\longleftarrow$
$⟹$	$\Longrightarrow$ 或 $\implies$
$⟸$	$\Longleftarrow$
$⟺$	$\Longleftrightarrow$
$\rightharpoonup$	$\rightharpoonup$
$\leftharpoonup$	$\leftharpoonup$
$\rightharpoondown$	$\rightharpoondown$
$\leftharpoondown$	$\leftharpoondown$
$\swarrow$	$\swarrow$
$\nearrow$	$\nearrow$
$\nwarrow$	$\nwarrow$
$\searrow$	$\searrow$
$\mapsto$	$\mapsto$
$⟼$	$\longmapsto$

离散数学符号

符号	公式	名称
$\neg$	$\neg$	非
$\wedge$	$\wedge$	合取，且
$\vee$	$\vee$	析取，或
$\to$	$\rightarrow$	充分条件
$\leftarrow$	$\leftarrow$	必要条件
$\leftrightarrow$	$\leftrightarrow$	充要条件

戴帽符号（各种帽子）

戴帽符号	公式语言
$\hat{A}$	$\hat{A}$
$\hat{A}$	$\widehat{A}$
$\check{A}$	$\check{A}$
$\check{A}$	$\widecheck{A}$
$\breve{A}$	$\breve{A}$
$\tilde{A}$	$\tilde{A}$
$\tilde{A}$	$\widetilde{A}$
$\overline{A}$	$\overline{A}$
$\underline{A}$	$\underline{A}$
$\overleftarrow{A}$	$\overleftarrow{A}$
$\overrightarrow{A}$	$\overrightarrow{A}$
$\overbrace{A}$	$\overbrace{A}$
$\underbrace{A}$	$\underbrace{A}$
$\stackrel{a}{b}$	$\overset{a}{b}$
$\underset{a}{b}$	$\underset{a}{b}$

特殊符号

上述内容仅包含一些常用公式及符号，一些不常用的符号可以查找官方文档获取，此处提供一个比较全的LaTeX符号博客：链接，供大家参考。

下方展示一些不常用特殊符号：

无穷大符号：$\infty$
$\infty$

领结符号：$\bowtie$
$\bowtie$

帽：$\hat x$
$\hat{x}$

范数：$\ell_p$
${\ell }_p$

箭头备注：$\xrightarrow{f}$
$\stackrel{f}{\to }$

上备注：$\overset{def}{=}$
$\stackrel{def}{=}$

下备注：$\underset{x\in S\subseteq X}{max}$
$\underset{x\in S\subseteq X}{\max }$

And so on.