您现在的位置是:主页 > news > 建一个门户网站多少钱/公司营销策划方案
建一个门户网站多少钱/公司营销策划方案
![]() admin2025/6/1 20:28:08【news】
admin2025/6/1 20:28:08【news】
简介建一个门户网站多少钱,公司营销策划方案,乌鲁木齐做网站公司,团建智慧登陆官网文章目录1 原函数与不定积分的概念1.1 原函数1.2 原函数存在定理1.3 不定积分2 不定积分的性质3 基本积分表4 例题后记1 原函数与不定积分的概念 1.1 原函数 定义1 如果在区间I上,可导函数F(x)的导航为f(x),即对任一x∈Ix\in Ix∈I,都有 F′…
文章目录
- 1 原函数与不定积分的概念
- 1.1 原函数
- 1.2 原函数存在定理
- 1.3 不定积分
- 2 不定积分的性质
- 3 基本积分表
- 4 例题
- 后记
1 原函数与不定积分的概念
1.1 原函数
定义1 如果在区间I上,可导函数F(x)的导航为f(x),即对任一x∈Ix\in Ix∈I,都有
F′(x)=f(x)或者dF(x)=f(x)dxF^{'}(x)=f(x)或者dF(x)=f(x)dxF′(x)=f(x)或者dF(x)=f(x)dx,
那么函数F(x)就称为f(x)(或者f(x)dxf(x)dxf(x)dx)在区间I上的一个原函数。
1.2 原函数存在定理
原函数存在定理 如果函数f(x)在区间I上连续,那么在区间I存在可导函数F(x),使得对于任一x∈Ix\in Ix∈I都有
F′(x)=f(x)F^{'}(x)=f(x)F′(x)=f(x)
连续函数一定有原函数
- 如果f(x)有一个原函数,那么f(x)就有无限多个原函数
- F(x)+CF(x)+CF(x)+C可以表示f(x)f(x)f(x)的任意一个原函数,其中C为任意常数
1.3 不定积分
定义2 在区间I上,函数f(x)f(x)f(x)的带有任意常数项的原函数称为f(x)(或f(x)dx)f(x)(或f(x)dx)f(x)(或f(x)dx)在区间I上的不定积分,记做
∫f(x)dx\int{f(x)dx}∫f(x)dx
其中∫\int∫称为积分号,f(x)f(x)f(x)称为被积函数,f(x)dxf(x)dxf(x)dx称为被积表达式,x称为积分变量。
注:
- 若F(x)为f(x)F(x)为f(x)F(x)为f(x)的一个原函数,则∫f(x)dx=F(x)+C\int{f(x)dx}=F(x)+C∫f(x)dx=F(x)+C,其中C为任意常数。
- ∫f(x)dx\int{f(x)dx}∫f(x)dx表示f(x)f(x)f(x)的任意一个原函数,是一种运算。
例2 求∫1xdx\int \frac{1}{x}dx∫x1dx
解:当x>0时,(lnx)′=1x,所以∫1xdx=lnx+C当x<0时,(ln(−x))′=1−x⋅−1=1x,∫1xdx=ln(−x)+C综上∫1xdx=ln∣x∣+C解:\\ 当x\gt0时,(\ln x)^{'}=\frac{1}{x},所以\int \frac{1}{x}dx=\ln x+C \\ 当x\lt0时,(\ln(-x))^{'}=\frac{1}{-x}\cdot-1=\frac{1}{x},\int \frac{1}{x}dx=\ln(-x)+C \\ 综上\int \frac{1}{x}dx=\ln|x|+C \\ 解:当x>0时,(lnx)′=x1,所以∫x1dx=lnx+C当x<0时,(ln(−x))′=−x1⋅−1=x1,∫x1dx=ln(−x)+C综上∫x1dx=ln∣x∣+C
2 不定积分的性质
设F(x)为f(x)在区间I上的一个原函数
性质1 d[∫f(x)dx]dx=f(x)或d[∫f(x)dx]=f(x)dx\frac{d[\int f(x)dx]}{dx}=f(x)或 d[\int f(x)dx]=f(x)dxdxd[∫f(x)dx]=f(x)或d[∫f(x)dx]=f(x)dx
性质2 ∫F′(x)dx=F(x)+C或∫dF(x)=F(x)+C\int F^{'}(x)dx=F(x)+C或\int dF(x)=F(x)+C∫F′(x)dx=F(x)+C或∫dF(x)=F(x)+C
性质3 设函数f(x)及g(x)的原函数存在,则
∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx\int{[f(x)+g(x)]dx}=\int{f(x)dx}+\int{g(x)dx}∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx
证明:上式右端求导,[∫f(x)dx+∫g(x)dx]′=[∫f(x)dx]′+[∫g(x)dx]′=f(x)+g(x)所以右端也是f(x)+g(x)的不定积分证明:\\ 上式右端求导,[\int{f(x)dx}+\int{g(x)dx}]^{'}=[\int{f(x)dx}]^{'}+[\int{g(x)dx}]^{'}\\ =f(x)+g(x) \\ 所以右端也是f(x)+g(x)的不定积分 证明:上式右端求导,[∫f(x)dx+∫g(x)dx]′=[∫f(x)dx]′+[∫g(x)dx]′=f(x)+g(x)所以右端也是f(x)+g(x)的不定积分
注:性质3对于有限个函数都是成立的。
性质4 设函数f(x)的原函数存在,kkk为非零常数,则
∫kf(x)dx=k∫f(x)dx\int{kf(x)dx}=k\int{f(x)dx}∫kf(x)dx=k∫f(x)dx
3 基本积分表
①$\int{kdx}=kx+C $
②∫xudx=xu+1u+1+C\int{x^udx}=\frac{x^{u+1}}{u+1}+C∫xudx=u+1xu+1+C ③∫dxx=ln∣x∣+C\int{\frac{dx}{x}}=\ln|x|+C∫xdx=ln∣x∣+C
④∫11+x2dx=arctanx+C\int{\frac{1}{1+x^2}dx}=\arctan x+C∫1+x21dx=arctanx+C ⑤∫11−x2dx=arcsinx+C\int{\frac{1}{\sqrt{1-x^2}}dx}=\arcsin x+C∫1−x21dx=arcsinx+C
⑥∫cosxdx=sinx+C\int{\cos xdx}=\sin x+C∫cosxdx=sinx+C ⑦∫sinxdx=−cosx+C\int{\sin xdx}=-\cos x+C∫sinxdx=−cosx+C
⑧∫1sin2xdx=∫sec2xdx=tanx+C\int{\frac{1}{\sin^2x}dx}=\int{\sec^2xdx}=\tan x+C∫sin2x1dx=∫sec2xdx=tanx+C ⑨∫1cos2xdx=∫csc2xdx=−cotx+C\int{\frac{1}{\cos^2x}dx}=\int{\csc^2xdx}=-\cot x+C∫cos2x1dx=∫csc2xdx=−cotx+C
⑩∫secxtanxdx=secx+C\int{\sec x\tan xdx}=\sec x+C∫secxtanxdx=secx+C ⑪∫cscxcotxdx=−cscx+C\int{\csc x\cot xdx}=-\csc x+C∫cscxcotxdx=−cscx+C
⑫∫exdx=ex+C\int{e^xdx}=e^x+C∫exdx=ex+C ⑬∫axdx=axlna+C\int{a^xdx}=\frac{a^x}{\ln a}+C∫axdx=lnaax+C
4 例题
例1 ∫(x−1)3x2dx\int{\frac{(x-1)^3}{x^2}dx}∫x2(x−1)3dx
解:∫(x−1)3x2dx=∫x3−3x2+3x−1x2=∫xdx−∫3dx+∫3x−∫1x2=12x2−3x+3ln∣x∣+1x+C解:\\ \int{\frac{(x-1)^3}{x^2}dx}=\int{\frac{x^3-3x^2+3x-1}{x^2}}\\ =\int{xdx}-\int{3dx}+\int{\frac{3}{x}}-\int{\frac{1}{x^2}}\\ =\frac{1}{2}x^2-3x+3\ln|x|+\frac{1}{x}+C 解:∫x2(x−1)3dx=∫x2x3−3x2+3x−1=∫xdx−∫3dx+∫x3−∫x21=21x2−3x+3ln∣x∣+x1+C
例2 ∫2x4+x2+3x2+1dx\int{\frac{2x^4+x^2+3}{x^2+1}dx}∫x2+12x4+x2+3dx
解:利用多项式相除,得2x2+1,余4,有∫2x4+x2+3x2+1dx=∫(2x2−1+4x2+1)dx=∫2x2dx−∫1dx+∫4x2+1dx=2x33−x+4arctanx+C解:\\ 利用多项式相除,得2x^2+1,余4,有\\ \int{\frac{2x^4+x^2+3}{x^2+1}dx}=\int{(2x^2-1+\frac{4}{x^2+1})dx}\\ =\int{2x^2dx}-\int{1dx}+\int{\frac{4}{x^2+1}dx}=\frac{2x^3}{3}-x+4\arctan x+C 解:利用多项式相除,得2x2+1,余4,有∫x2+12x4+x2+3dx=∫(2x2−1+x2+14)dx=∫2x2dx−∫1dx+∫x2+14dx=32x3−x+4arctanx+C
多项式相除,如下图4-1所示: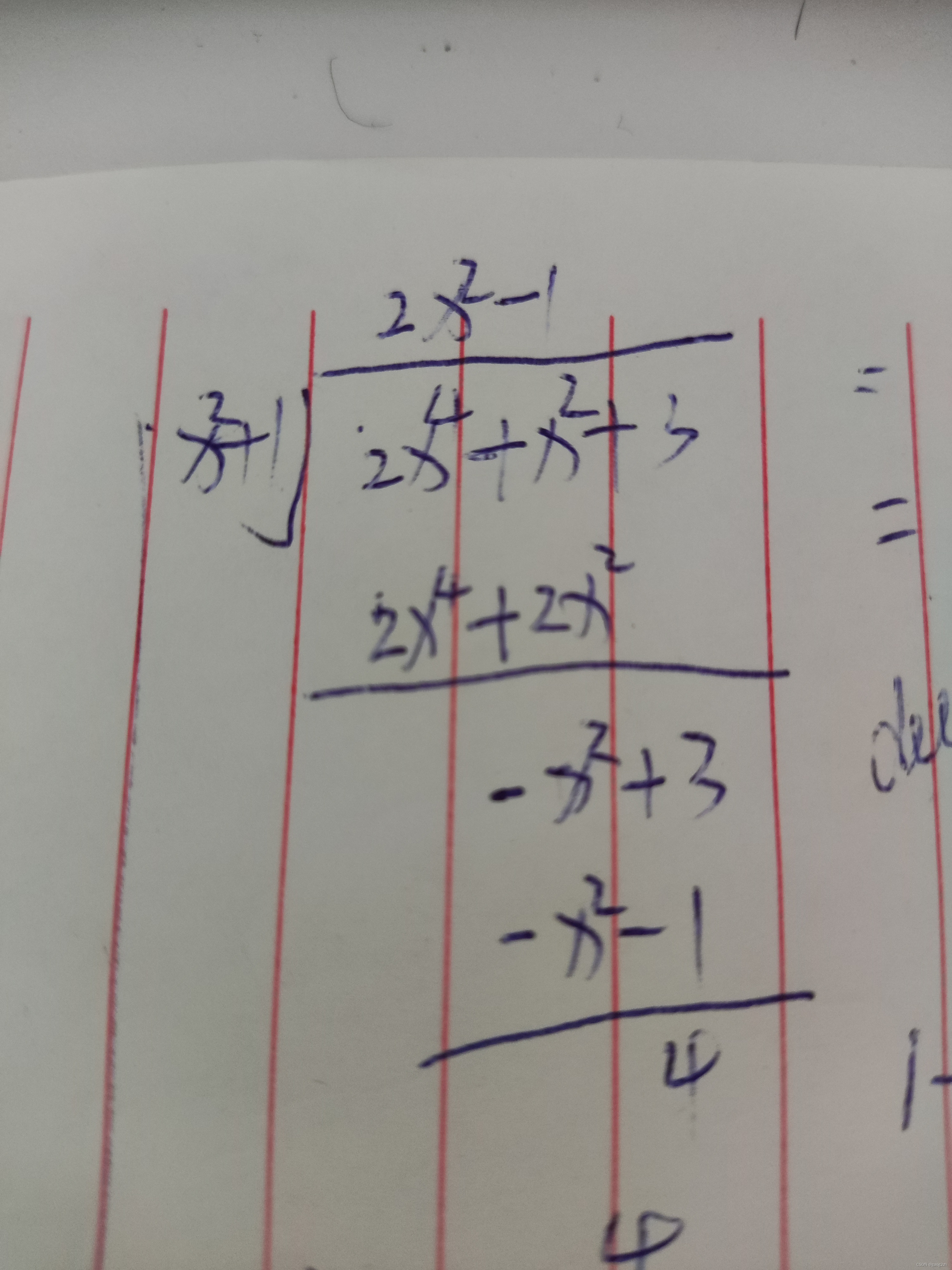
后记
❓QQ:806797785
⭐️文档笔记地址:https://gitee.com/gaogzhen/math
参考:
[1]同济大学数学系.高等数学 第七版 上册[M].北京:高等教育出版社,2014.7.P184~p193.
[2]【梨米特】同济七版《高等数学》全程教学视频|纯干货知识点解析,应该是全网最细|微积分 | 高数[CP/OL].2020-04-16.p27.








