您现在的位置是:主页 > news > 网站开发能封装成app吗/实体店铺引流推广方法
网站开发能封装成app吗/实体店铺引流推广方法
![]() admin2025/5/30 6:19:23【news】
admin2025/5/30 6:19:23【news】
简介网站开发能封装成app吗,实体店铺引流推广方法,做企业官网的流程,做技术分享网站 盈利文章目录算法符号说明Hamilton方程物理解释一些性质可逆 ReversibilityH的不变性保体积 Volume preservation辛 Symplecticness离散化Hamilton方程 leapfrog方法Eulers methodModified Eulers methodLeapfrog methodMCMC概率与Hamiltonian, 正则(canonical)分布HMC算法HMC保持正…
文章目录
- 算法
- 符号说明
- Hamilton方程
- 物理解释
- 一些性质
- 可逆 Reversibility
- H的不变性
- 保体积 Volume preservation
- 辛 Symplecticness
- 离散化Hamilton方程 leapfrog方法
- Euler's method
- Modified Euler's method
- Leapfrog method
- MCMC
- 概率与Hamiltonian, 正则(canonical)分布
- HMC算法
- HMC保持正则分布不变的证明 detailed balance
- 遍历性 Ergodicty
- HMC的一个例子及优势
- HMC在实际中的应用和理论
- 线性变换
- HMC的调整ϵ,L\epsilon, Lϵ,L
- 结合HMC与其它MCMC
- Scaling with dimensionality
- HMC的扩展和变种
- 分割
- 处理约束
- Langevin method, LMC
- Windows of states
- 代码
Neal R. M. , MCMC Using Hamiltonian Dynamics[J]. arXiv: Computation, 2011: 139-188.
@article{neal2011mcmc,
title={MCMC Using Hamiltonian Dynamics},
author={Neal, Radford M},
journal={arXiv: Computation},
pages={139–188},
year={2011}}
Hamiltonian Monte Carlo-wiki
算法
先把算法列一下.
Input: 初始值qqq, 步长ϵ\epsilonϵ与leapfrog迭代次数LLL.
- 令q(0)=qq^{(0)} = qq(0)=q;
- 循环迭代直到停止条件满足(以下第ttt步):
- 从标准正态分布中抽取ppp, q=q(t−1)q = q^{{(t-1)}}q=q(t−1), p(t−1)=pp^{(t-1)} = pp(t−1)=p.
- p=p−ϵ∇qU(q)/2,(alg.1)\tag{alg.1} p = p- \epsilon \nabla_q U(q) / 2, p=p−ϵ∇qU(q)/2,(alg.1)
- 重复 i=1,2,…,Li=1,2,\ldots, Li=1,2,…,L:
- q=q+ϵ∇pH(p),(alg.2)\tag{alg.2} q = q + \epsilon \nabla_pH(p), q=q+ϵ∇pH(p),(alg.2)
- 如果i≠Li \not = Li=L:
p=p−ϵ∇qU(q).(alg.3)\tag{alg.3} p = p- \epsilon \nabla_q U(q). p=p−ϵ∇qU(q).(alg.3)
- p=p−ϵ∇qU(q)/2,p∗=−p,q∗=q.(alg.4)\tag{alg.4} p = p- \epsilon \nabla_q U(q) / 2, \quad p^* = -p, q^*=q. p=p−ϵ∇qU(q)/2,p∗=−p,q∗=q.(alg.4)
- 计算接受概率
α=min{1,exp(−H(q∗,p∗)+H(q∗,p∗)}.(alg.5)\tag{alg.5} \alpha = \min \{ 1, \exp(-H(q^*,p^*) + H(q^*, p^*)\}. α=min{1,exp(−H(q∗,p∗)+H(q∗,p∗)}.(alg.5) - 从均匀分布U(0,1)U(0,1)U(0,1)中抽取uuu, 如果u<αu<\alphau<α, q(t)=q∗q^{(t)}=q^*q(t)=q∗, 否则q(t)=q(t−1)q^{(t)}=q^{(t-1)}q(t)=q(t−1).
output: {p(t),q(t)}\{p^{(t)},q^{(t)}\}{p(t),q(t)}.
注: 1中的标准正态分布不是唯一的, 但是文中选的便是这个. 4中的p∗=−pp^*=-pp∗=−p在实际编写程序的时候可以省去.
符号说明
因为作者从物理方程的角度给出几何解释,所以这里给出的符号一般有俩个含义:
| 符号 | 概率 | 物理 |
|---|---|---|
| qqq | 随机变量,服从我们所在意的分布 | 冰球的位置 |
| ppp | 用以构造马氏链的额外的变量 | 冰球的动量(mv) |
| U(q)U(q)U(q) | …与我们所在意的分布有关 | 冰球的势能 |
| K(p)K(p)K(p) | … | 冰球的动能 |
| H(q,p)H(q, p)H(q,p) | 与我们所在意的分布有关 | H(q,p)=U(q)+K(p)H(q, p) = U(q) + K(p)H(q,p)=U(q)+K(p) |
Hamilton方程
物理解释
Hamilton方程(i=1,2,…,di=1,2,\ldots, di=1,2,…,d, ddd是维度):
dqidt=∂H∂pi(2.1)\tag{2.1} \frac{dq_i}{dt} = \frac{\partial H}{\partial p_i} dtdqi=∂pi∂H(2.1)
dpidt=−∂H∂qi(2.2)\tag{2.2} \frac{dp_i}{dt} = -\frac{\partial H}{\partial q_i} dtdpi=−∂qi∂H(2.2)
这个东西怎么来的, 大概是因为H(q,p)=U(q)+K(p)H(q, p) = U(q)+K(p)H(q,p)=U(q)+K(p), 如果机械能守恒, 那么随着时间ttt的变化H(q,p)H(q, p)H(q,p)应该是一个常数, 所以其关于t的导数应该是0.
dHdt=∑i[∂H∂pidpidt+∂H∂qidqidt]=(∇pH)Tp˙+(∇qH)Tq˙=0,\frac{dH}{dt} = \sum_i [\frac{\partial H}{\partial p_i} \frac{dp_i}{dt}+\frac{\partial H}{\partial q_i}\frac{dq_i}{dt}] = (\nabla_p H)^T \dot{p}+(\nabla_qH)^T \dot{q} = 0, dtdH=i∑[∂pi∂Hdtdpi+∂qi∂Hdtdqi]=(∇pH)Tp˙+(∇qH)Tq˙=0,
其中p˙=(∂p1/∂t,…,∂pd/∂t)\dot{p}=(\partial{p_1}/\partial t, \ldots, \partial p_d / \partial t)p˙=(∂p1/∂t,…,∂pd/∂t).
而(2.1)(2.1)(2.1), 左边是速度q˙=v\dot{q} = vq˙=v, 右边
∇pH=∇pK=∇p∣p∣22m=pm=v=q˙.\nabla_p H = \nabla_p K = \nabla_p \frac{|p|^2}{2m} = \frac{p}{m} = v=\dot{q}. ∇pH=∇pK=∇p2m∣p∣2=mp=v=q˙.
不过,估计是先有的(2.2)再有的H吧, 就先这么理解吧. 需要一提的是, K(p)K(p)K(p)通常定义为
K(p)=pTM−1p/2,K(p)=p^TM^{-1}p/2, K(p)=pTM−1p/2,
其中MMM是对称正定的, 后面我们可以看到, 这种取法与正态分布相联系起来.
此时:
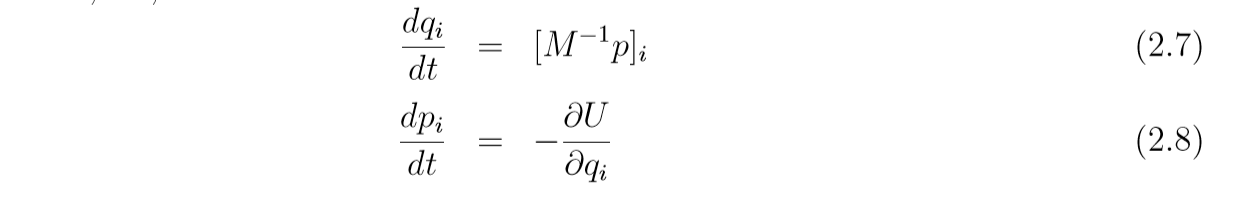
一些性质
可逆 Reversibility
映射Ts:(q(t),p(t))↦(q(t+s),p(t+s))T_s: (q(t), p(t)) \mapsto (q(t+s), p(t+s))Ts:(q(t),p(t))↦(q(t+s),p(t+s))是一一的,这个我感觉只能从物理的解释上理解啊, 一个冰球从一个点到另一个点, 现在H确定, 初值确定, 不就相当于整个轨迹都确定了吗, 那从哪到哪自然是一一的, 也就存在逆T−sT_{-s}T−s, 且只需:
dqidt=−∂H∂pi,\frac{dq_i}{dt} = -\frac{\partial H}{\partial p_i}, dtdqi=−∂pi∂H,
dpidt=−(−∂H∂qi).\frac{dp_i}{dt} = -(-\frac{\partial H}{\partial q_i}). dtdpi=−(−∂qi∂H).
H的不变性
即
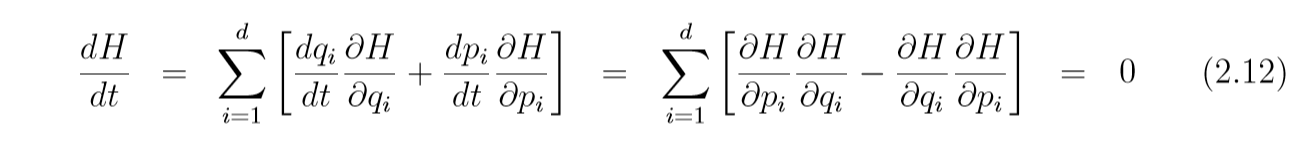
当然, 因为我们的算法是离散化的, 所以这个性质只是在ϵ\epsilonϵ比较小的时候近似保持.
保体积 Volume preservation
即假设区域R={(q,p)}R=\{(q,p)\}R={(q,p)}在映射TtT_tTt的作用下为Rt={(q(t),p(t)}R_t=\{(q(t), p(t)\}Rt={(q(t),p(t)}, 则二者的体积相同, 均为VVV.
定义
v(t)=∫RtdV=∫Rdet(∂Tt∂z)dV,v(t)= \int_{R_t} dV = \int_{R} \det( \frac{\partial T_t}{\partial z}) dV, v(t)=∫RtdV=∫Rdet(∂z∂Tt)dV,
其中z=(q,p)z = (q, p)z=(q,p). 又
z(t)=Ttz=z+tJ∇H(z)+O(t2),z(t) = T_tz = z+t J\nabla H(z) + \mathcal{O}(t^2), z(t)=Ttz=z+tJ∇H(z)+O(t2),
其中
f:=dzdt=J∇H(z),J=(0d×dId×d−Id×d0d×d).f:=\frac{dz}{dt} = J\nabla H(z), \\ J = \left ( \begin{array}{ll} 0_{d \times d} & I_{d\times d} \\ -I_{d\times d} & 0_{d \times d} \end{array}\right ). f:=dtdz=J∇H(z),J=(0d×d−Id×dId×d0d×d).
所以
∂Tt∂z=I+∂f∂zt+O(t2),\frac{\partial{T_t}}{\partial z} = I + \frac{\partial f}{\partial z}t + \mathcal{O}(t^2), ∂z∂Tt=I+∂z∂ft+O(t2),
又对于任意方阵AAA,
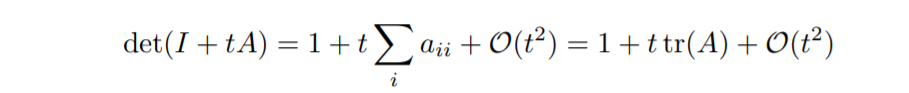
所以
det(∂Tt∂z)=1+tr(∂f/∂z)t+O(t2),\det (\frac{\partial{T_t}}{\partial z} ) = 1 + \mathrm{tr}(\partial f / \partial z) t + \mathcal{O}(t^2), det(∂z∂Tt)=1+tr(∂f/∂z)t+O(t2),
且tr(∂f/∂z)=divf\mathrm{tr}(\partial f / \partial z)=\mathrm{div} ftr(∂f/∂z)=divf, 于是
dvdt∣t=0=∫RdivfdV.\frac{d v}{ d t} |_{t=0} = \int_{R}\mathrm{div} f \: d V. dtdv∣t=0=∫RdivfdV.
又
divf=divJ∇H(z)=Jdiv∇H(z)=∑i=1d[∂∂q∂H∂pi−∂∂p∂H∂qi]=0.\mathrm{div}f = \mathrm{div} J\nabla H(z) = J \mathrm{div} \nabla H(z) = \sum_{i=1}^d [\frac{\partial}{\partial q}\frac{\partial H}{\partial p_i}-\frac{\partial}{\partial p}\frac{\partial H}{\partial q_i}] = 0. divf=divJ∇H(z)=Jdiv∇H(z)=i=1∑d[∂q∂∂pi∂H−∂p∂∂qi∂H]=0.
对于t=t0t=t_0t=t0, 我们都可以类似的证明dv(t0)/dt=0dv(t_0)/dt=0dv(t0)/dt=0, 所以v(t)v(t)v(t)是常数.
这部分的证明参考自
Here
辛 Symplecticness

离散化Hamilton方程 leapfrog方法
下面四幅图, 是U(q)=q2/2,K(p)=p2/2U(q)=q^2/2, K(p)=p^2/2U(q)=q2/2,K(p)=p2/2, 起始点为(q,p)=(0,1)(q, p) = (0, 1)(q,p)=(0,1).
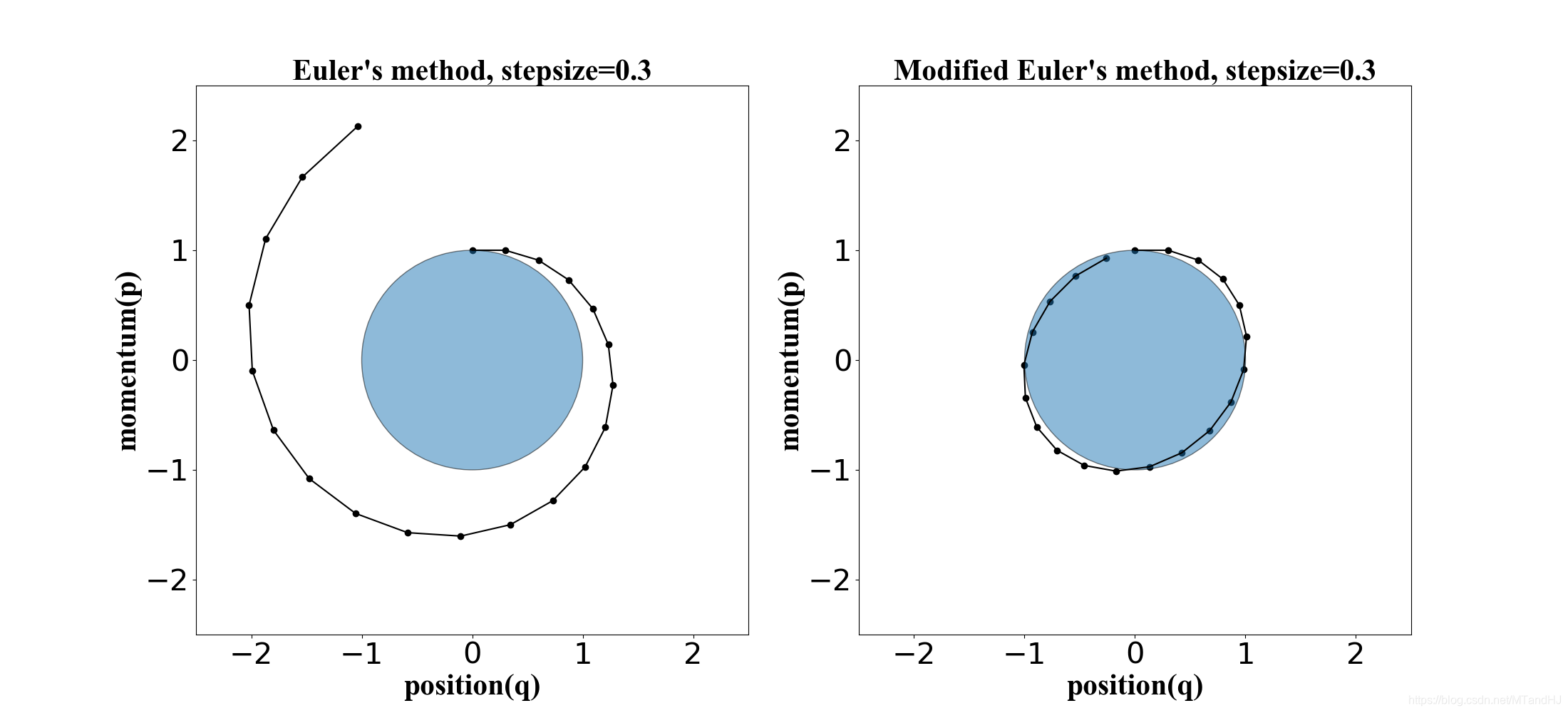
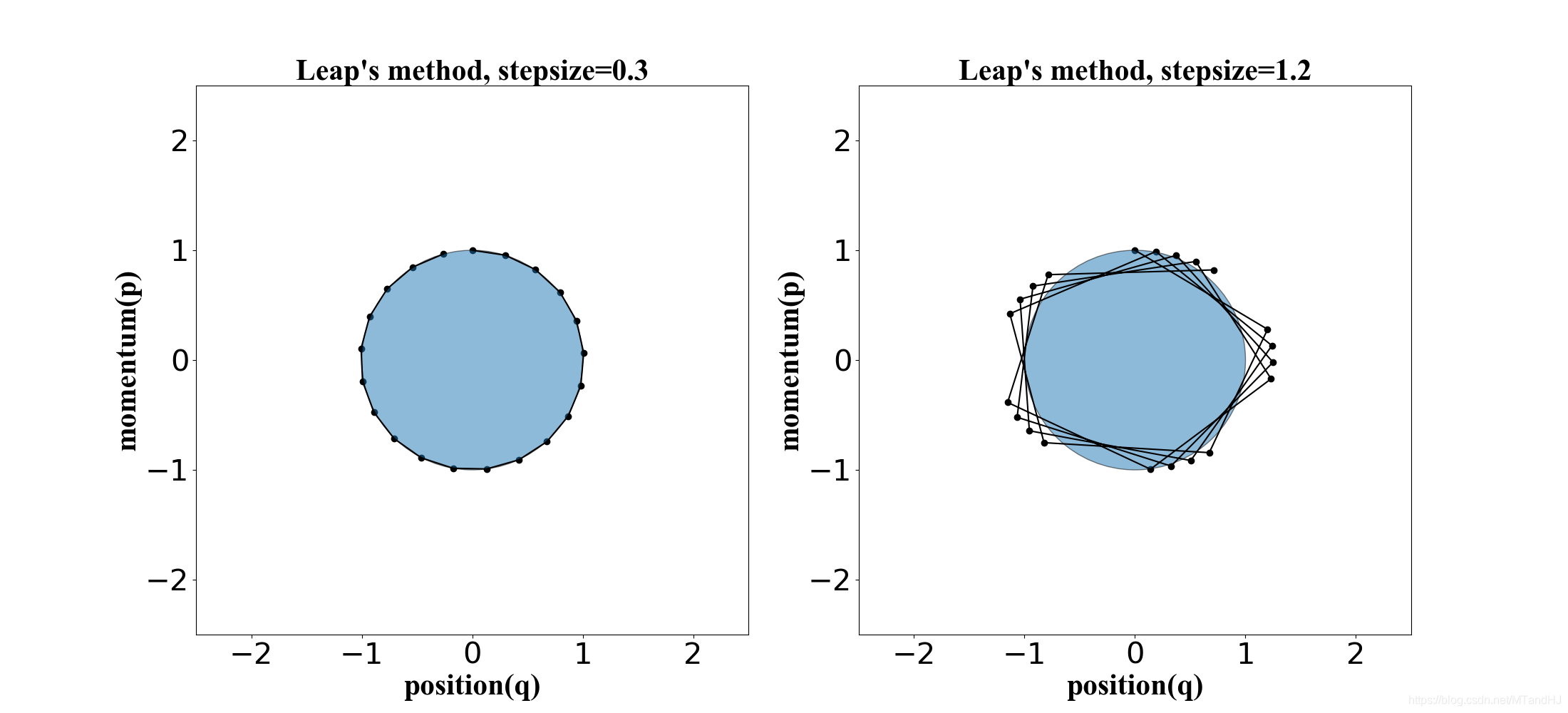
Euler’s method
如果假定K(p)=∑i=1dpi22miK(p) = \sum_{i=1}^d \frac{p_i^2}{2m_i}K(p)=∑i=1d2mipi2,
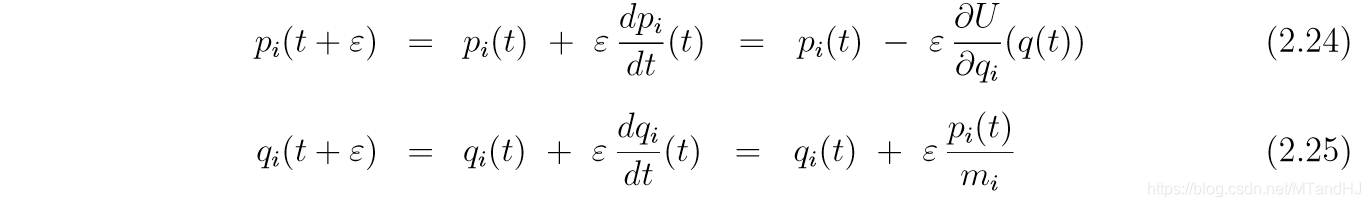
Modified Euler’s method
仅有一个小小的变动,
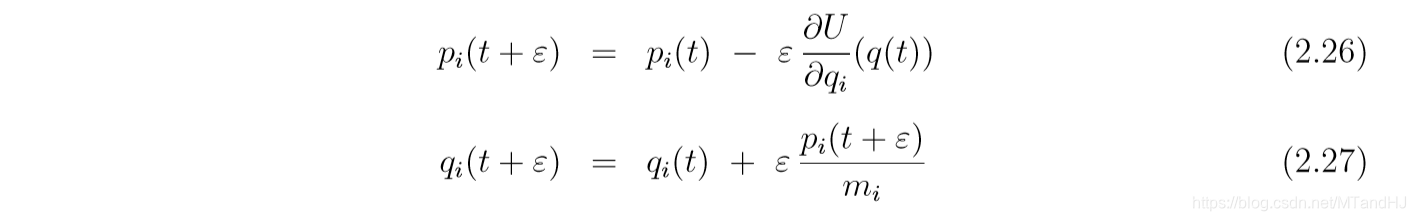
Leapfrog method
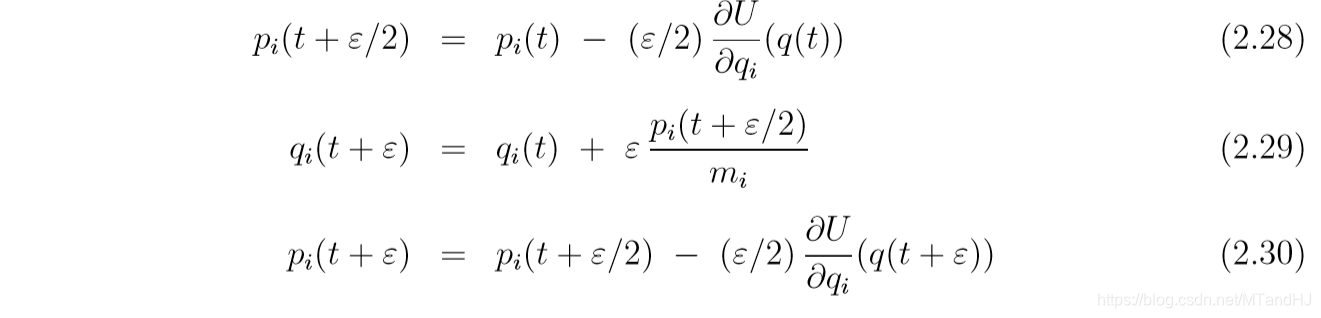
注意到, 在实际编写程序的时候, 除了第一步和最后一步, 我们可以将ppp的俩个半步合并成一步.
另外从右下角的图可以发现, 因为离散化的缘故, H(q,p)H(q, p)H(q,p)的值是有偏差的. 但是Leapfrog 方法和 modified Euler方法都是保体积的, 因为每步更新都只改变一个量, 可以验证其雅可比行列式为1.
MCMC
概率与Hamiltonian, 正则(canonical)分布
如何将分布于Hamilton方程联系在一起? 假如, 我们关心的是qqq的分布P(q)P(q)P(q), 则我们构造一个容易采样的分布P(q)P(q)P(q),
P(q,p)=1Zexp(−H(q,p)/T),(3.2)\tag{3.2} P(q, p) = \frac{1}{Z}\exp(-H(q,p)/T), P(q,p)=Z1exp(−H(q,p)/T),(3.2)
其中ZZZ是规范化的常数, TTT一般取1. 从(3.2)中容易得到H(q,p)H(q,p)H(q,p). 事实上此时q,pq, pq,p是独立的(这么写是说明直接构造P(q,p)P(q, p)P(q,p)也是可以的), 则可以分别
P(q)=1Z1exp(−U(q)/T),P(p)=1Z2exp(−K(p)/T).P(q) = \frac{1}{Z_1}\exp(-U(q)/T), \\ P(p) = \frac{1}{Z_2}\exp(-K(p)/T). P(q)=Z11exp(−U(q)/T),P(p)=Z21exp(−K(p)/T).
在贝叶斯统计中, 有
U(q)=−log[π(q)L(D∣q)],U(q) = -\log [\pi (q) L(D|q)], U(q)=−log[π(q)L(D∣q)],
其中DDD为数据, LLL为似然函数, 与文章中不同, 文章中是L(q∣D)L(q|D)L(q∣D), 应该是笔误.
HMC算法
就是开头提到的算法, 但是其中有一些地方值得思考. (alg.4)我们令p∗=−pp^*=-pp∗=−p, 这一步在实际中是不起作用的, 既然K(p)=K(−p)K(p)=K(-p)K(p)=K(−p)而且在下轮中我们重新采样ppp, 我看网上的解释是为了理论, 取反这一部分使得proposal是对称的, 是建议分布g(p∗,q∗∣p,q)=g(p,q∣p∗,q∗)g(p^*, q^*|p, q)=g(p, q| p^*, q^*)g(p∗,q∗∣p,q)=g(p,q∣p∗,q∗)? 不是很懂.
关于这个问题的讨论
有点明白了, 首先因为Leapfrog是确定的, 所以P(q∗,p∗∣q,p)P(q^*, p^*|q, p)P(q∗,p∗∣q,p)非0即1:
P(q∗,p∗∣q,p)=δ(q∗,p∗,q,p)={1,TLϵ(q,p)=q∗,p∗,0,TLϵ(q,p)≠q∗,p∗.P(q^*, p^*|q, p) = \delta(q^*,p^*,q,p) = \left \{ \begin{array}{ll} 1, & T_{L\epsilon} (q, p) = q^*, p^*, \\ 0, & T_{L\epsilon} (q, p) \not = q^*, p^*. \end{array} \right. P(q∗,p∗∣q,p)=δ(q∗,p∗,q,p)={1,0,TLϵ(q,p)=q∗,p∗,TLϵ(q,p)=q∗,p∗.
为了P(q∗,p∗∣q,p)=P(q,p∣q∗,p∗)P(q^*, p^*|q, p)=P(q, p|q^*, p^*)P(q∗,p∗∣q,p)=P(q,p∣q∗,p∗), 如果不取反肯定不行, 因为他就会往下走, 取反的操作实际上就是在可逆性里提到的, 在同样的操作下, q∗,p∗q^*, p^*q∗,p∗会回到q,pq, pq,p. 于是MH接受概率就退化成了M接受概率. 但是前文也提到了, 取反的操作, 只有在K(p)=K(−p)K(p)=K(-p)K(p)=K(−p)的情况下是成立的.
HMC保持正则分布不变的证明 detailed balance
假设{Ak}\{A_k\}{Ak}是(q,p)∈R2d(q, p) \in \mathbb{R}^{2d}(q,p)∈R2d空间的一个分割, 其在L次leapfrog的作用, 及取反的操作下的像为{Bk}\{B_k\}{Bk}, 由于可逆性, {Bk}\{B_k\}{Bk}也是一个分割, 且有相同的体积VVV(保体积性),则
P(Ai)T(Bj∣Ai)=P(Bj)T(Ai∣Bj).P(A_i) T(B_j|A_i) = P(B_j)T(A_i|B_j). P(Ai)T(Bj∣Ai)=P(Bj)T(Ai∣Bj).
实际上i≠ji\not =ji=j是时候是显然的, 因为二者都是0. 因为HHH是连续函数, 当VVV变得很小的时候, HHH在XXX区域上的值相当于常数HXH_XHX, 于是
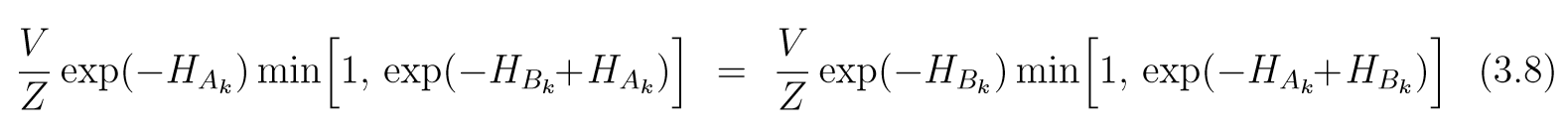
所以(3.7)成立.
Detailed balance:
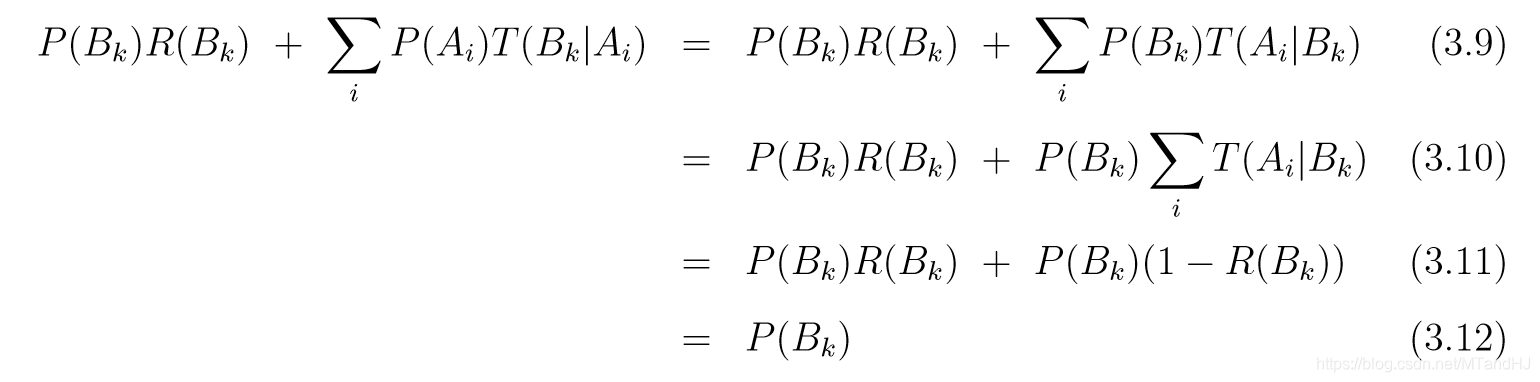
其中R(X)R(X)R(X)是当前状态属于XXX, 拒绝提议的(q∗,p∗)(q^*,p^*)(q∗,p∗)的概率. 注意∑iT(Ai∣Bk)=T(Ak∣Bk)=1−R(Bk)\sum_{i} T(A_i|B_k)=T(A_k|B_k)=1-R(B_k)∑iT(Ai∣Bk)=T(Ak∣Bk)=1−R(Bk). 看上面的连等式可能会有点晕, 注意到, 左端实际上是概率P{q(t),p(t))∈Bk}P\{q^{(t)}, p^{(t)}) \in B_k\}P{q(t),p(t))∈Bk}, 最右端是P{(q(t−1),p(t−1))∈Bk}P\{(q^{(t-1)}, p^{(t-1)}) \in B_k\}P{(q(t−1),p(t−1))∈Bk}, 这样就能明白啥意思了.
遍历性 Ergodicty
马氏链具有遍历性才会收敛到一个唯一的分布上(这部分不了解), HMC是具有这个性质的, 只要LLL和ϵ\epsilonϵ选的足够好. 但是如果选的不过也会导致坏的结果, 比如上面的图, p2+q2=1p^2+q^2=1p2+q2=1, 如果我们选择了Lϵ≈2πL\epsilon \approx 2\piLϵ≈2π, 那么我们的Leapfrog总会带我们回到原点附近, 这就会导致比较差的结果.
HMC的一个例子及优势
下图是:
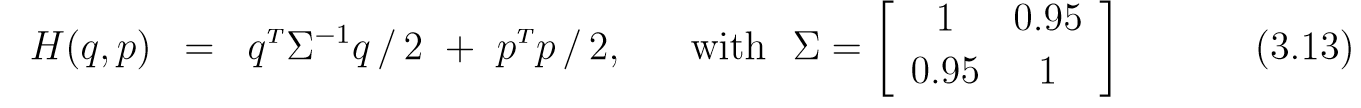
ϵ=0.25,L=30,q=[−1.5,−1.55]T,p=[−1,1T]\epsilon=0.25, L=30, q = [-1.5, -1.55]^T, p=[-1, 1^T]ϵ=0.25,L=30,q=[−1.5,−1.55]T,p=[−1,1T].
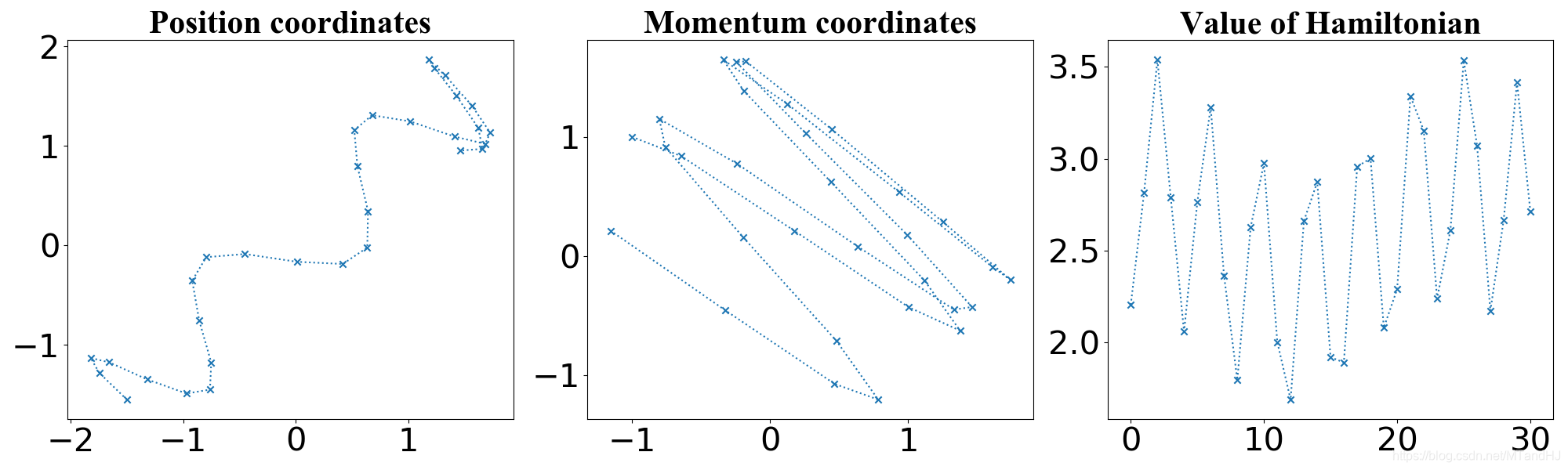
相关系数由0.950.950.95改为0.980.980.98, ϵ=0.18,L=20\epsilon=0.18, L=20ϵ=0.18,L=20, 随机游走取的协方差矩阵为对角阵, 标准差为0.180.180.18, HMC生成ppp的为标准正态分布.
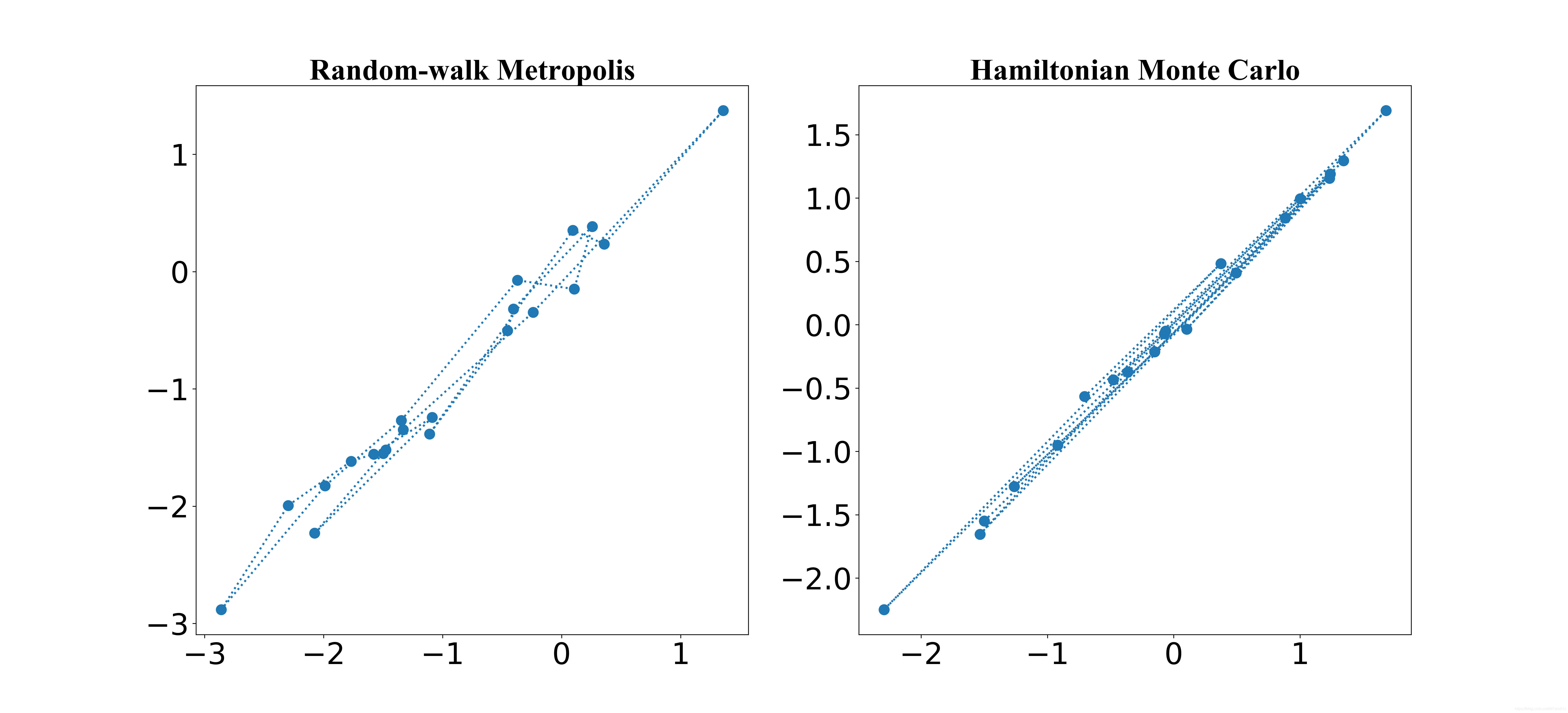
文章中提到, HMC较Randomwalk的优势在于,Randomwalk对协方差很敏感, 而且太大会导致接受率很低, 太小俩俩之间的相关性又会太高.
HMC在实际中的应用和理论
线性变换
有些时候, 我们会对变量施加线性映射q′=Aqq'=Aqq′=Aq(AAA非奇异方阵), 此时新的密度函数P′(q′)=P(A−1q′)/∣det(A)∣P'(q') = P(A^{-1}q') / |\det (A)|P′(q′)=P(A−1q′)/∣det(A)∣, 其中P(q)P(q)P(q)是qqq的密度函数, 相应的我们需要令U′(q′)=U(A−1q′)U'(q')=U(A^{-1}q')U′(q′)=U(A−1q′).
如果我们希望线性变化前后不会是的情况变得"更糟", 一个选择是p′=(AT)−1pp'=(A^T)^{-1}pp′=(AT)−1p,则K′(p′)=K(ATp′)K'(p')=K(A^Tp')K′(p′)=K(ATp′), 如果K(p)=pTM−1p/2K(p) = p^TM^{-1}p / 2K(p)=pTM−1p/2, 则
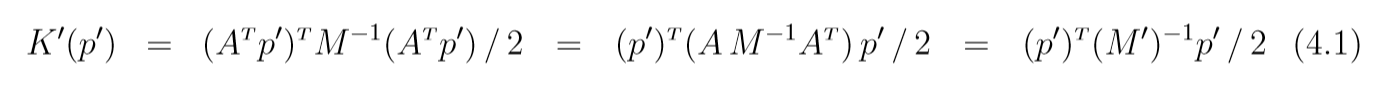
其中M′=(AM−1AT)−1=(A−1)TMA−1M' = (AM^{-1}A^T)^{-1}=(A^{-1})^TMA^{-1}M′=(AM−1AT)−1=(A−1)TMA−1. 此时(q′,p′)(q', p')(q′,p′)的更新会使得原先的(q,p)(q,p)(q,p)的更新保持, 即
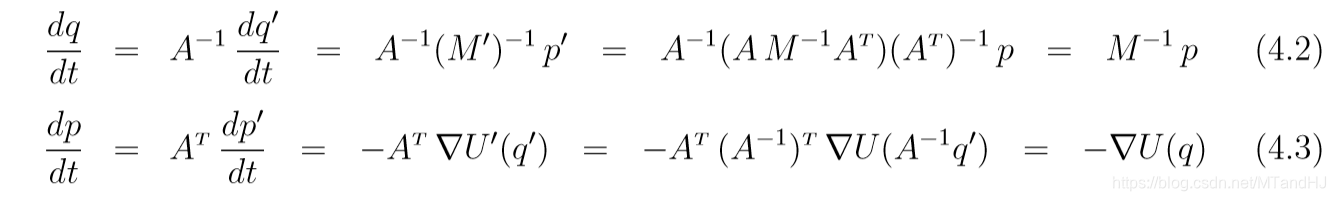
所以(q,p)(q, p)(q,p)本质上按照原来的轨迹发生着变化.
设想, 我们对qqq的协方差矩阵有一个估计Σ\SigmaΣ, 且近似服从高斯分布, 我们可以对其做Cholesky分解Σ=LLT\Sigma=LL^TΣ=LLT, 并且令q′=L−1qq'=L^{-1} qq′=L−1q, 则q′q'q′的各分量之间就相互独立了, 那么我们很自然的一个选择是K(p)=pTp/2K(p)=p^Tp/2K(p)=pTp/2, 那么q′q'q′的各分量的独立性能够保持.
另一个做法是, 保持qqq不变, 但是K(p)=pTΣp/2K(p) = p^T \Sigma p / 2K(p)=pTΣp/2, 此时q′=L−1q,p′=(LT)−1pq'=L^{-1}q, p'=(L^{T})^{-1}pq′=L−1q,p′=(LT)−1p, 则相当于
K(p′)=(p′)TM′−1p′,M′=(L−1LLT(L−1)T)−1=I.K(p')=(p')^T{M'}^{-1}p', \quad M' = (L^{-1}LL^T(L^{-1})^T)^{-1}=I. K(p′)=(p′)TM′−1p′,M′=(L−1LLT(L−1)T)−1=I.
所以俩个方法是等价的.
HMC的调整ϵ,L\epsilon, Lϵ,L
HMC对ϵ,L\epsilon, Lϵ,L的选择比较严苛.
预先的实验
我们可以对一些ϵ,L\epsilon,Lϵ,L进行实验, 观察轨迹, 虽然这个做法可能产生误导, 另外在抽样过程中随机选择ϵ,L\epsilon, Lϵ,L是一个不错的选择.
stepsize ϵ\epsilonϵ
ϵ\epsilonϵ的选择很关键, 如果太大, 会导致低的接受率, 如果太小, 不仅会造成大量的计算成本, 且如果此时LLL也很小, 那么HMC会缺乏足够的探索.
考虑下面的例子:
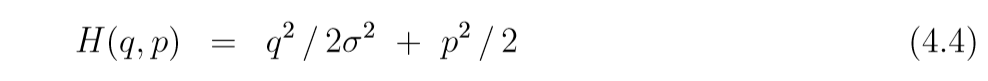
每一次leapfrog将(q(t),p(t))(q(t), p(t))(q(t),p(t))映射为(q(t+s),p(t+s))(q(t+s), p(t+s))(q(t+s),p(t+s)), 则
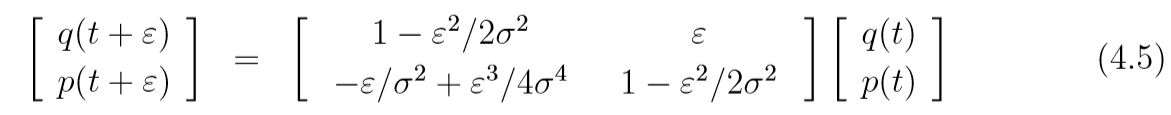
(q,p)(q, p)(q,p)是否稳定, 关键在于系数矩阵的特征值的模(?还是实部)是否小于1, 特征值为
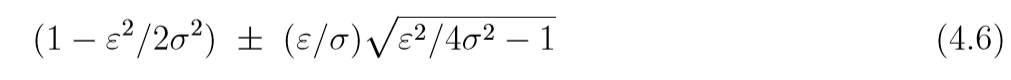
当ϵ>2σ\epsilon>2\sigmaϵ>2σ的时候,(4.6)有一个实的大于1的特征值, 当ϵ<2σ\epsilon < 2 \sigmaϵ<2σ的时候, 特征值是复制, 且模为:
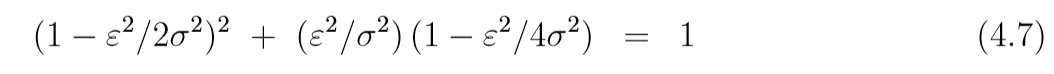
所以, 我们应当选择ϵ<2σ\epsilon < 2\sigmaϵ<2σ.
在多维问题中, K(p)=pTp/2K(p)=p^Tp/2K(p)=pTp/2,如果q<0q<0q<0且协方差矩阵为Σ\SigmaΣ, 我们可以取协方差矩阵的最小特征值(非零?)作为步长. 如果K(p)=pTM−1p/2K(p)=p^TM^{-1}p/2K(p)=pTM−1p/2, 我们可以通过线性变化将其转换再考虑.
tracjectory length LLL
如何选择LLL也是一个问题, 我们需要足够大的LLL使得每次的探索的足够的, 以便能够模拟出独立的样本, 但是正如前面所讲, 大的LLL不仅会带来计算成本, 而且可能会导致最后结果在起点附近(由周期性带来的麻烦). 而且LLL没法通过轨迹图正确的选择. 一个不错的想法是在一个小的区间内随机选择LLL, 这样做可能会减少由于周期性带来的麻烦.
多尺度
我们可以利用qqq的缩放信息, 为不同的qiq_iqi添加给予不同的ϵi\epsilon_iϵi. 比方说在K(p)=pTp/2K(p)=p^Tp/2K(p)=pTp/2的前提下, 应该对qiq_iqi放大sis_isi倍, 即q′=q/siq'= q / s_iq′=q/si(ppp不变).
等价的, 可以令K(p)=pTM−1p/2,mi=1/si2K(p) = p^TM^{-1}p / 2, m_i = 1/ s_i^2K(p)=pTM−1p/2,mi=1/si2(qqq不变), 相当于qi′=qi/si,p′=sipq_i'=q_i/s_i, p'=s_ipqi′=qi/si,p′=sip, 则
mi′=si(1/si2)si=1m_i' = s_i (1/ s_i^2)s_i=1mi′=si(1/si2)si=1, 所以K(p′)=(p′)Tp′/2K(p')=(p')^Tp'/2K(p′)=(p′)Tp′/2. 这么做就相当于一次leapfrog为:
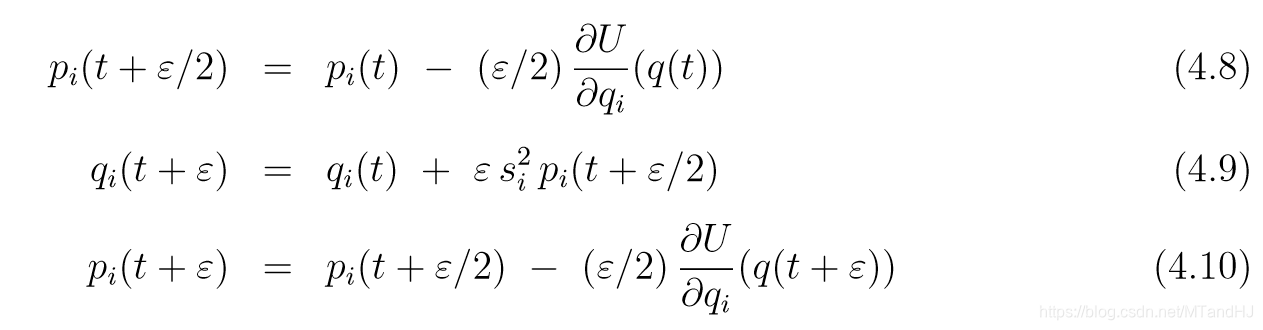
结合HMC与其它MCMC
当我们所关心的变量是离散的, 或者其对数概率密度(U(q)U(q)U(q))的导数难以计算的时候, 结合其它MCMC是有必要的.
Scaling with dimensionality
U(q)=∑ui(qi)U(q) = \sum u_i(q_i)U(q)=∑ui(qi)的情况
如果U(q)=∑ui(qi)U(q)=\sum u_i(q_i)U(q)=∑ui(qi), 且uiu_iui之间相互独立(?), 这种假设是可行的, 因为之前已经讨论过, 对于qqq其协方差矩阵为Σ\SigmaΣ, 我们可以通过线性变化使其对角化, 且效能保持.
Cruetz指出, 任何的Metropolis形式的算法在采样密度函数P(x)=1Zexp(−E(x))P(x)=\frac{1}{Z}\exp(-E(x))P(x)=Z1exp(−E(x))的时候都满足:
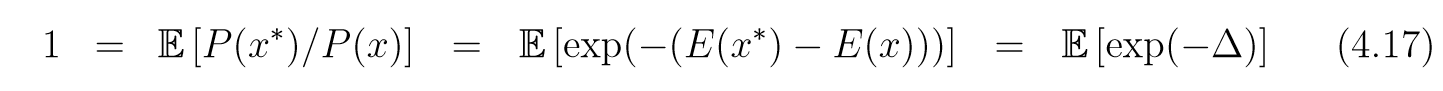
其中xxx表现在的状态, 而x∗x^*x∗表提议. 则根据Jensen不等式可知:
1=E[exp(Δ)]≥exp(E[−Δ]),1 = \mathbb{E}[\exp(\Delta)] \ge \exp(\mathbb{E}[-\Delta]), 1=E[exp(Δ)]≥exp(E[−Δ]),
所以E[−Δ]≤0\mathbb{E}[-\Delta]\le 0E[−Δ]≤0,
E[Δ]≥0.(4.18)\tag{4.18} \mathbb{E}[\Delta] \ge 0. E[Δ]≥0.(4.18)
在U(q)=∑ui(qi)U(q) = \sum u_i(q_i)U(q)=∑ui(qi)的情况下, 令Δ1:=E(x∗)−E(x)\Delta_1:=E(x^*)-E(x)Δ1:=E(x∗)−E(x), x=qi,E(x)=ui(qi)x=q_i, E(x)=u_i(q_i)x=qi,E(x)=ui(qi)或者x=(qi,pi),E(x)=ui(qi)=pi2/2x=(q_i, p_i), E(x)=u_i(q_i)=p_i^2/2x=(qi,pi),E(x)=ui(qi)=pi2/2. 对于整个状态, 我们则用Δd\Delta_dΔd表示, 则Δd\Delta_dΔd是所有Δ1\Delta_1Δ1的和. 既然Δ\DeltaΔ的平均值均为正, 这会导致接受概率min(1,exp(−Δd)\min (1, \exp(-\Delta_d)min(1,exp(−Δd)的减小(随着维度的增加), 除非以减小步长作为代价, 或者建议分布的宽度进一步降低(即x,x∗x,x^*x,x∗尽可能在一个区域内).
因为exp(−Δ1)≈1−Δ1+Δ12/2\exp(-\Delta_1) \approx 1 -\Delta_1+\Delta_1^2 / 2exp(−Δ1)≈1−Δ1+Δ12/2, 再根据(4.17)得:
E[Δ1]≈E[Δ12]/2.(4.19)\tag{4.19} \mathbb{E} [\Delta_1] \approx \mathbb{E} [\Delta_1^2]/2. E[Δ1]≈E[Δ12]/2.(4.19)
故Δ1\Delta_1Δ1的方差约是均值的两倍(Δ1\Delta_1Δ1足够小的时候), 类似的也作用与Δd\Delta_dΔd. 为了有一个比较好的接受率, 我们应当控制Δd\Delta_dΔd的均值在1左右(小于?), 此时exp(−1)≈0.3679\exp(-1)\approx0.3679exp(−1)≈0.3679.
HMC的全局误差(标准差)在O(ϵ2)\mathcal{O}(\epsilon^2)O(ϵ2)级别, 所以Δ12\Delta_1^2Δ12应当在ϵ4\epsilon^4ϵ4级别, 所以E[Δ1]\mathbb{E}[\Delta_1]E[Δ1]也应当在ϵ4\epsilon^4ϵ4级别, 则E[Δd]\mathbb{E}[\Delta_d]E[Δd]在dϵ4d\epsilon^4dϵ4级别上, 所以为了保持均值为1左右, 我们需要令ϵ\epsilonϵ正比于d−1/4d^{-1/4}d−1/4, 相应的LLL为d1/4d^{1/4}d1/4.
文章中还有关于Randomwalk的分析, 这里不多赘述了.
HMC的扩展和变种
这个不一一讲了, 提一下
分割
假如HHH能够分解成:

那么我们可以一个一个来处理, 相当于T1,ϵ∘T2,ϵ,∘⋯∘Tk−1,ϵ∘Tk,ϵT_{1, \epsilon} \circ T_{2, \epsilon}, \circ \cdots \circ T_{k-1, \epsilon} \circ T_{k, \epsilon}T1,ϵ∘T2,ϵ,∘⋯∘Tk−1,ϵ∘Tk,ϵ. 这个做法依旧是保体积的(既然每一个算子都是保体积的), 但是如果希望其可逆(对称), 这就要求Hi(q,p)=Hk−i+1(q,p).H_i(q, p)=H_{k-i+1}(q, p).Hi(q,p)=Hk−i+1(q,p). 这个有很多应用场景:
比如U(q)=U0(q)+U1(q)U(q) = U_0(q)+U_1(q)U(q)=U0(q)+U1(q), 其中计算U0U_0U0如果是容易的, 我们可以作如下分解:
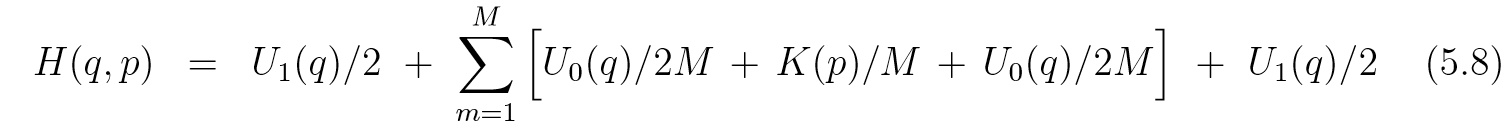
此时有3M+23M+23M+2项, H1(q,p)=Hk(q,p)=U1(q)/2H_1(q, p) = H_k(q, p)=U_1(q)/2H1(q,p)=Hk(q,p)=U1(q)/2, H3i−1=H3i+1=U0(q)/2MH_{3i-1}=H_{3i+1}=U_0(q)/2MH3i−1=H3i+1=U0(q)/2M, H3i=K(p)/MH_{3i}=K(p)/MH3i=K(p)/M. 此时对于中间部分, 相当于步长变小了,误差自然会小.
当处理大量数据, 并用到似然函数的时候:

不过文章中说这个分解是不对称的, 可明明是对称的啊.
处理约束
有些时候, 我们对qqq有约束条件, 比方q>v,q<wq >v, q<wq>v,q<w等等, 直接给算法:

Langevin method, LMC
假设我们使用K(p)=(1/2)∑pi2K(p)=(1/2)\sum p_i^2K(p)=(1/2)∑pi2, ppp从标准正态分布中采样, 每次我们只进行一次leapfrog变计算接受概率, 即
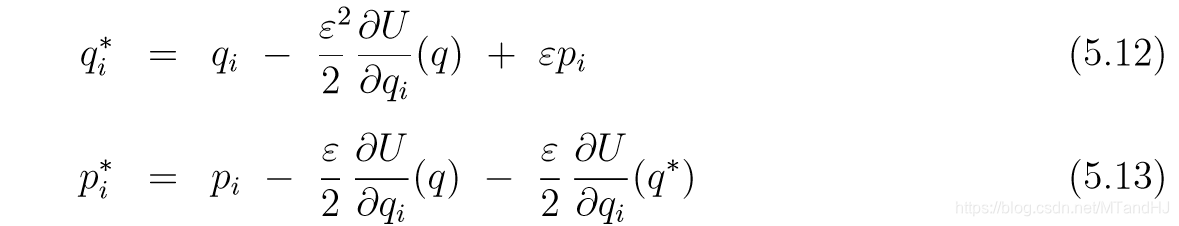
以及其接受概率:
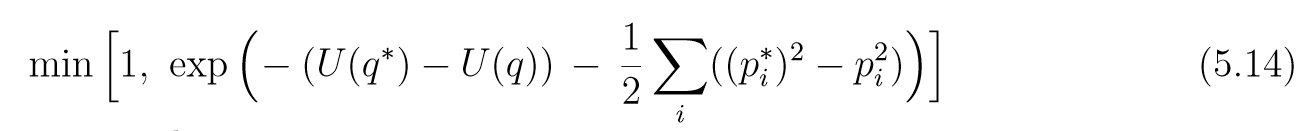
Windows of states
这个方法试图将HHH的曲线平滑来提高接受率.
我们可以通过任意(q,p)(q, p)(q,p)构造一列[(q0,p0),…,(qW−1,pW−1)][(q_0, p_0), \ldots, (q_{W-1}, p_{W-1})][(q0,p0),…,(qW−1,pW−1)]. 首先从{0,1,…,W−1}\{0, 1, \ldots, W-1\}{0,1,…,W−1}中等概率选一个数, 这个数代表(q,p)(q, p)(q,p)在序列中的位置, 记为(qs,ps)(q_s, p_s)(qs,ps), 则其前面的可以通过leapfrog (−ϵ-\epsilon−ϵ)产生, 后面的通过leapfrog(+ϵ+\epsilon+ϵ)产生. 所以任意列的概率密度为:
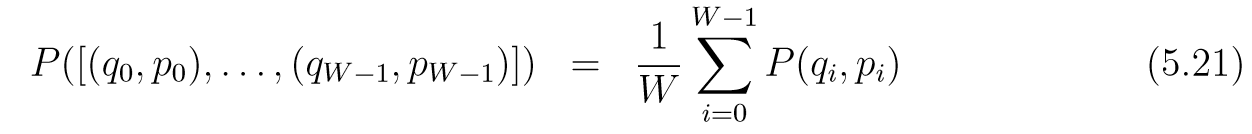
然后从(qW−1,pW−1)(q_{W-1}, p_{W-1})(qW−1,pW−1)出发, 通过L-W+1步leapfrog(+ϵ+\epsilon+ϵ)获得[qW,pW,…,(qL,pL)][q_W,p_W,\ldots, (q_L, p_L)][qW,pW,…,(qL,pL)]并定义提议序列为[(qL,−pL),…,(qL−W+1,pL−W+1)][(q_L, -p_{L}), \ldots, (q_{L-W+1}, p_{L-W+1)}][(qL,−pL),…,(qL−W+1,pL−W+1)],计算接受概率:
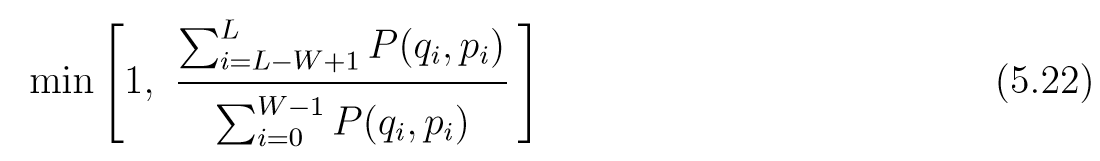
其中P(q,p)∝exp(−H(q,p))P(q, p)\propto \exp(-H(q,p))P(q,p)∝exp(−H(q,p)). 设拒绝或者接受后的状态为:[(q0+,p0+),…,(qW−1+,pW−1+)][(q_0^+, p_0^+), \ldots, (q_{W-1}^+, p_{W-1}^+)][(q0+,p0+),…,(qW−1+,pW−1+)], 依照概率

抽取(qe+,pe+)(q_e^+, p_e^+)(qe+,pe+), 这个就是(q,p)(q,p)(q,p)后的下一个状态.
文中说这么做分布不变, 因为:
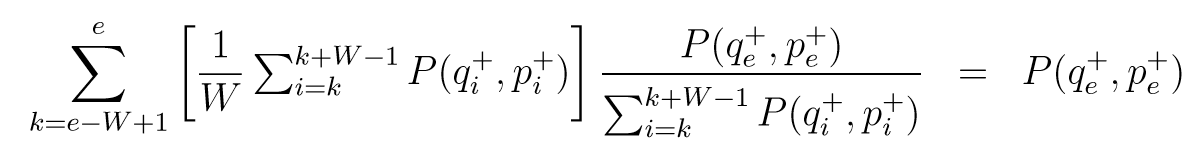
如果没理解错, 前面的部分就是(qe+,pe+)(q_e^+, p_e^+)(qe+,pe+)出现在最开始的序列中的概率, 但是中间的接受概率哪里去了? 总不能百分百接受吧…
代码
import numpy as np
from collections.abc import Iterator, Callable
from scipy import stats
class Euler:"""Euler方法"""def __init__(self, grad_u, grad_k, epsilon):self.grad_u = grad_uself.grad_k = grad_kself.epsilon = epsilondef start(self, p, q, steps):trajectory_p = [p]trajectory_q = [q]for t in range(steps):temp = p - self.epsilon * self.grad_u(q) # 更新一步Pq = q + self.epsilon * self.grad_k(p) # 更新一步qp = temptrajectory_p.append(p)trajectory_q.append(q)return trajectory_p, trajectory_qdef modified_start(self, p, q, steps):"""启动!:param p::param q::param steps: 步数:return: p, q"""trajectory_p = [p]trajectory_q = [q]for t in range(steps):p = p - self.epsilon * self.grad_u(q) #更新一步Pq = q + self.epsilon * self.grad_k(p) #更新一步qtrajectory_p.append(p)trajectory_q.append(q)return trajectory_p, trajectory_q
class Leapfrog:"""Leapfrog 方法"""def __init__(self, grad_u, grad_k, epsilon):self.grad_u = grad_uself.grad_k = grad_kself.epsilon = epsilonself.trajectory_q = []self.trajectory_p = []def start(self, p, q, steps):self.trajectory_p.append(p)self.trajectory_q.append(q)for t in range(steps):p = p - self.epsilon * self.grad_u(q) / 2q = q + self.epsilon * self.grad_k(p)p = p - self.epsilon * self.grad_u(q) / 2self.trajectory_q.append(q)self.trajectory_p.append(p)return p, q
class HMC:"""HMC方法 start为进行一次accept_prob: 计算接受概率hmc: 完整的过程acc_rate: 接受概率"""def __init__(self, grad_u, grad_k, hamiltonian, epsilon):assert isinstance(grad_u, Callable), "function needed..."assert isinstance(grad_k, Callable), "function needed..."assert isinstance(hamiltonian, Callable), "function needed..."self.grad_u = grad_uself.grad_k = grad_kself.hamiltonian = hamiltonianself.epsilon = epsilonself.trajectory_q = []self.trajectory_p = []def start(self, p, q, steps):self.trajectory_p.append(p)self.trajectory_q.append(q)p = p - self.epsilon * self.grad_u(q) / 2for t in range(steps-1):q = q + self.epsilon * self.grad_k(p)p = p - self.epsilon * self.grad_u(q)q = q + self.epsilon * self.grad_k(p)p = p - self.epsilon * self.grad_u(q) / 2p = -preturn p, qdef accept_prob(self, p1, q1, p2, q2):""":param p1: 原先的:param q1::param p2: 建议的:param q2::return:"""p1 = np.exp(self.hamiltonian(p1, q1))p2 = np.exp(self.hamiltonian(p2, q2))alpha = min(1, p1 / p2)return alphadef hmc(self, generate_p, q, iterations, steps):assert isinstance(generate_p, Iterator), "Invalid generate_p"self.trajectory_q = [q]p = next(generate_p)self.trajectory_p = [p]count = 0.for t in range(iterations):tempp, tempq = self.start(p, q, steps)if np.random.rand() < self.accept_prob(p, q, tempp, tempq):p = temppq = tempqself.trajectory_p.append(p)self.trajectory_q.append(q)count += 1p = next(generate_p)self.acc_rate = count / iterationsreturn self.trajectory@propertydef trajectory(self):return np.array(self.trajectory_p), \np.array(self.trajectory_q)class Randomwalk:"""walk: 完整的过程, 实际上Metropolis更新似乎就是start中steps=1, 一开始将文章的意思理解错了, 不过将错就错, 这样子也能增加一下灵活性."""def __init__(self, pdf, sigma):assert isinstance(pdf, Callable), "function needed..."self.pdf = pdfself.sigma = sigmaself.trajectory = []def start(self, q, steps=1):for t in range(steps):q = stats.multivariate_normal.rvs(mean=q,cov=self.sigma)return qdef accept_prob(self, q1, q2):""":param q1: 原始:param q2: 建议:return:"""p1 = self.pdf(q1)p2 = self.pdf(q2)alpha = min(1, p2 / p1)return alphadef walk(self, q, iterations, steps=1):self.trajectory = [q]count = 0.for t in range(iterations):temp = self.start(q, steps)if np.random.rand() < self.accept_prob(q, temp):q = tempcount += 1self.trajectory.append(q)self.acc_rate = count / iterationsreturn np.array(self.trajectory)







