深圳极速网站建设定制/网页一键生成app软件

 

H - XOR

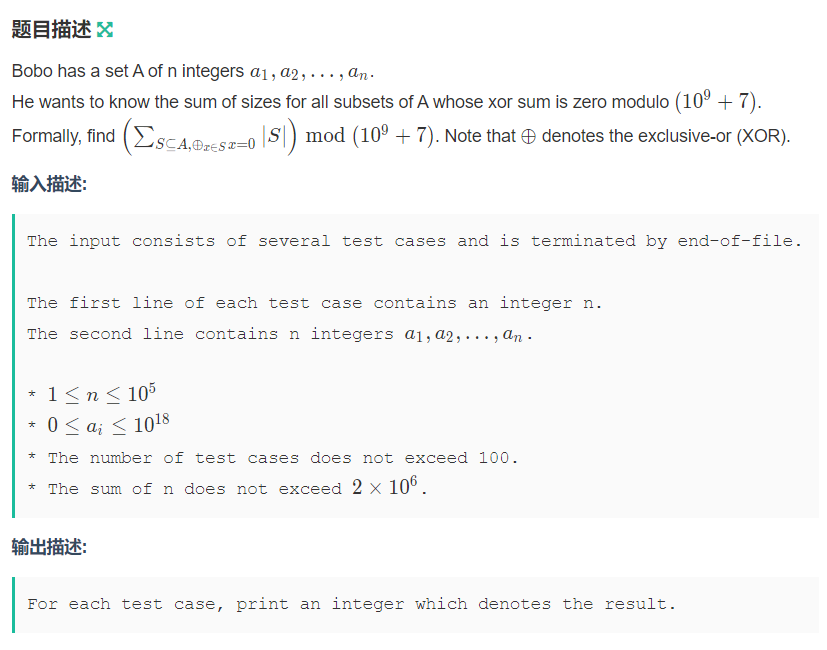
题意：给定n个整数，求所有异或和为0的子集的大小和。

思路：看到异或和，差不多就要往线性基上想。如果一些数异或和为0，肯定是线性基里的一些数和线性基外的一些数异或得到的，因为线性基外的数都能由线性基里的数异或得到。

先对n个数求线性基lb，设线性基大小为r。

1.线性基外的数的贡献：剩下 (n-r) 个数在线性基外。对于每一个线性基外的数，它可以和剩下的 (n-r-1) 的数任意组合，这种组合有 2^(n-r-1)，所以总共有的贡献 (n-r) * 2^(n-r-1)。

2.线性基内的数的贡献：对于每一个线性基内的数，如果有一个不包含它的线性基（由除它外的n-1数组成）能把它表示出来，那么它也就相当于是另一个线性基外的数，他的贡献也是 2^(n-r-1)。如果该数不能被剩下n-1个数的线性基表示出来，那么它不会出现在任何子集里，它的贡献为0。

 

关于线性基的介绍，看了好几篇博客，这篇比较详细。

这类题基本都是一样的套路：

1. 最大异或和
2. 第 k 大异或和 / 异或和是第几大
3. 求所有异或值的和

 

AC代码：

#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int mod = 1e9+7;
typedef long long ll;ll pow(ll a, ll n) {ll res = 1;while(n) {if(n&1) res = res * a % mod;a = a * a % mod;n >>= 1;}return res;
}
struct LB { // 线性基模板ll a[65];int cnt;LB() {memset(a, 0, sizeof(a));}ll insert(ll x) {for(int i=60;i>=0;i--) {if((x>>i)&1) {if(!a[i]) {  // a[i] 不存在a[i] = x;++cnt;break;} else {x ^= a[i];}}}return x>0;}
};int main() {int n;while(scanf("%d", &n)!=EOF) {LB lb1, lb2;int r = 0;vector<ll> v1, v2;ll ai;for(int i=1;i<=n;i++) {scanf("%lld", &ai);if(lb1.insert(ai)) {v1.push_back(ai);} elselb2.insert(ai);}if(v1.size()==n) {printf("0\n");continue;}//线性基外的数的总贡献ll ans = 1LL* (n-v1.size())* pow(2, n-v1.size()-1) % mod;//枚举每个线性基内的数 for(int i=0;i<v1.size();i++) {LB tmp = lb2;for(int j=0;j<v1.size();j++) {if(i==j) continue;tmp.insert(v1[j]);  //生成除了v1[i]之外的线性基
            }//如果v[i]能被线性基组成，他就属于线性基外的数if(!tmp.insert(v1[i])) ans = (ans + pow(2, n-v1.size()-1)) % mod;}printf("%lld\n", ans);}return 0;
}