学习心得

（1）模型评估的Error=偏差+方差+噪声
（2）为了改进以往的梯度下降，我们可以自适应调整学习速率Adagrad、随机梯度下降法、特征缩放等方法
（3）回归的作业和numpy实现logistic回归识别是否为猪狗猫task在下一篇【李宏毅机器学习CP9】（task3下部分）PM2.5预测作业 + numpy实现神经网络logistic回归，注意逻辑回归是最基础也是最重要的模型：

通过逻辑回归能演化出很多模型：

• 逻辑回归=线性回归+sigmoid激活函数，从而将回归问题转换为分类问题
• 逻辑回归+矩阵分解，构成了推荐算法中常用的FM模型
• 逻辑回归+softmax，从而将二分类问题转化为多分类问题
• 逻辑回归还可以看做单层神经网络，相当于最简单的深度学习模型

一、误差Error分析

由于真实模型 $\hat{f}$ 我们不知道，所以只能通过收集 Pokemon精灵 的数据，然后通过 step1~step3 训练得到我们的理想模型 $f^{\ast }$，$f^{\ast }$ 其实是 $\hat{f}$ 的一个预估。

1.估测变量x的偏差和方差

偏差：平均模型（对用所有训练集得到的所有模型求平均值）与真实模型之间的差距
方差：用所有训练集得到的所有模型本身也各不相同，他们的变动水平即方差

知乎orangeprince用户的一个解答：
首先 Error = Bias + VarianceError反映的是整个模型的准确度，Bias反映的是模型在样本上的输出与真实值之间的误差，即模型本身的精准度，Variance反映的是模型每一次输出结果与模型输出期望之间的误差，即模型的稳定性。

举一个例子，一次打靶实验，目标是为了打到10环，但是实际上只打到了7环，那么这里面的Error就是3。具体分析打到7环的原因，可能有两方面：一是瞄准出了问题，比如实际上射击瞄准的是9环而不是10环；二是枪本身的稳定性有问题，虽然瞄准的是9环，但是只打到了7环。那么在上面一次射击实验中，Bias就是1,反应的是模型期望与真实目标的差距，而在这次试验中，由于Variance所带来的误差就是2，即虽然瞄准的是9环，但由于本身模型缺乏稳定性，造成了实际结果与模型期望之间的差距。

1）评估x的偏差bias

• 假设 $x$ 的平均值是 $\mu$，方差为 ${\sigma }^2$

评估平均值要怎么做呢？

• 首先拿到 $N$ 个样本点：{x1,x2,⋅⋅⋅,xN}\{x^1,x^2,···,x^N\}{x1,x2,⋅⋅⋅,xN}
• 计算平均值 $m$, 得到 $m=\frac{1}{N}{\sum }_n{x}^n\ne \mu$

但是如果计算很多组的 $m$ ，然后求 $m$ 的期望：
$$E[m]=E[\frac{1}{N}\sum x^n]=\frac{1}{N}\sum _{n}E[x^n]=\mu$$ 这个估计是无偏估计（unbiased）。
然后 $m$ 分布对于 $\mu$ 的离散程度（方差）：
$$Var[m]=\frac{{\sigma }^2}{N}$$，N越小则越离散：

2）评估x的方差variable

上面的$Biased$ $estimator$在维基百科上（https://en.wikipedia.org/wiki/Bias_of_an_estimator）有对应的计算过程：


用同一个model，在不同的训练集中找到的 $f^{\ast }$ 就是不一样的

2.不同模型情况

1）不同模型的方差

一次模型的方差就比较小的，也就是是比较集中，离散程度较小。而5次模型的方差就比较大，同理散布比较广，离散程度较大。

所以用比较简单的模型，方差是比较小的（就像射击的时候每次的时候，每次射击的设置都集中在一个比较小的区域内）。如果用了复杂的模型，方差就很大，散布比较开。

这也是因为简单的模型受到不同训练集的影响是比较小的。

2）不同模型的偏差

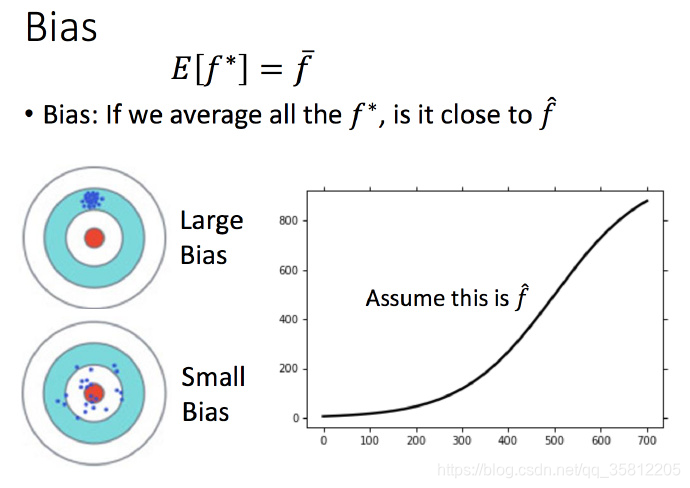
这里没办法知道真正的 $\hat{f}$，所以假设图中的那条黑色曲线为真正的 $\hat{f}$
结果可视化，一次平均的 $\bar{f}$ 没有5次的好，虽然5次的整体结果离散程度很高。

一次模型的偏差比较大，而复杂的5次模型，偏差就比较小。
直观的解释：简单的模型函数集的space比较小，所以可能space里面就没有包含靶心，肯定射不中。而复杂的模型函数集的space比较大，可能就包含的靶心，只是没有办法找到确切的靶心在哪，但足够多的，就可能得到真正的 f¯f¯。

每一个model就是一个function set，可以用上图的左下方的圈圈表示这个function set，即范围。一个简单的model的set是比较小的（可能就根本没有包含target），而上图左边的五次方方程曲线，这时的function set比较大。 虽然分布的比较散，没有办法找出target（数据少），但是比较分散在中心周围，平均起来能接近f¯。

3）方差VS偏差

将系列02中的误差拆分为偏差和方差。

• $Underfitting$欠拟合：简单模型（左边）是偏差（$bias$）比较大造成的误差
• $Overfitting$过拟合：复杂模型（右边）是方差（$variance$）过大造成的误差（过拟合，即在训练集表现良好，但是在测试集上很糟糕）

3.判断&分析

• 如果模型没有很好的训练训练集，就是偏差过大，也就是欠拟合
• 如果模型很好的训练训练集，即再训练集上得到很小的错误，但在测试集上得到大的错误，这意味着模型可能是方差比较大，就是过拟合。

对于欠拟合和过拟合，是用不同的方式来处理的

1）bias偏差大-欠拟合

此时应该重新设计模型。因为之前的函数集里面可能根本没有包含$f^{\ast }$。可以：

• 将更多的函数加进去，比如考虑高度重量，或者HP值等等。
• 或者考虑更多次幂、更复杂的模型。

如果此时强行再收集更多的data去训练，这是没有什么帮助的，因为设计的函数集本身就不好，再找更多的训练集也不会更好。

2）variance方差大-过拟合

• 简单粗暴的方法：更多的数据
  

• 但是很多时候不一定能做到收集更多的data。
  PS：很多种收集（调整）数据的方法，针对对问题的理解对数据集做调整。比如识别手写数字的时候，偏转角度的数据集不够，那就将正常的数据集左转15度，右转15度，类似这样的处理。

• 另一方法：正则化，使得参数越小越好（找到的曲线更平滑），也可以对$regularization$一项加上$weight$。但是正则化可能影响$bias$（曲线都平滑时可能就没包含目标的function）。

4.模型的选择

• 现在在偏差和方差之间就需要一个权衡
• 想选择的模型，可以平衡偏差和方差产生的错误，使得总错误最小

但是下面这件事最好不要做：

用训练集训练不同的模型，然后在测试集上比较错误，模型3的错误比较小，就认为模型3好。但实际上这只是你手上的测试集，真正完整的测试集并没有。比如在已有的测试集上错误是0.5，但有条件收集到更多的测试集后通常得到的错误都是大于0.5的。

1）交叉验证

图中public的测试集是已有的，private是没有的，不知道的。

• 交叉验证 就是将训练集再分为两部分，一部分作为训练集，一部分作为验证集。用训练集训练模型，然后再验证集上比较，确实出最好的模型之后（比如模型3），再用全部的训练集训练模型3，然后再用public的测试集进行测试，此时一般得到的错误都是大一些的。
• 不过此时会比较想再回去调一下参数，调整模型，让在public的测试集上更好，但不太推荐这样。

上述方法可能会担心将训练集拆分的时候分的效果比较差怎么办，可以用下面的方法。

2）N-折交叉验证

将训练集分成N份，比如分成3份。

比如在三份中训练结果Average错误是模型1最好，再用全部训练集训练模型1。

二、梯度下降

0.复习梯度下降

在回归问题的第三步中，需要解决下面的最优化问题：

$${\theta }^{\ast }=\underset{\theta }{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}L(\theta )\text{\hspace{1em}(1)}$$

• $L$ :lossfunction（损失函数）
• $\theta$ :parameters（参数）

这里的parameters是复数，即 $\theta$ 指代一堆参数，比如上篇说到的 $w$ 和 $b$ 。

我们要找一组参数 $\theta$ ，让损失函数越小越好，这个问题可以用梯度下降法解决：

假设 $\theta$ 有里面有两个参数 ${\theta }_1,{\theta }_2$
随机选取初始值

$${\theta }^0=\left[\begin{array}{c}{\theta }_1^0\\ {\theta }_2^0\end{array}\right]\text{\hspace{1em}(2)}$$

然后分别计算初始点处，两个参数对 $L$ 的偏微分，然后 ${\theta }^0$ 减掉 $\eta$ 乘上偏微分的值，得到一组新的参数。同理反复进行这样的计算。黄色部分为简洁的写法，$▽L(\theta )$ 即为梯度。

$\eta$ 叫做Learning rates（学习速率）

上图举例将梯度下降法的计算过程进行可视化。

1.优化算法

1）调整学习速率

小心翼翼地调整学习率

上图左边黑色为损失函数的曲线，假设从左边最高点开始，如果学习率调整的刚刚好，比如红色的线，就能顺利找到最低点。如果学习率调整的太小，比如蓝色的线，就会走的太慢，虽然这种情况给足够多的时间也可以找到最低点，实际情况可能会等不及出结果。如果 学习率调整的有点大，比如绿色的线，就会在上面震荡，走不下去，永远无法到达最低点。还有可能非常大，比如黄色的线，直接就飞出去了，更新参数的时候只会发现损失函数越更新越大。

虽然这样的可视化可以很直观观察，但可视化也只是能在参数是一维或者二维的时候进行，更高维的情况已经无法可视化了。

解决方法就是上图右边的方案，将参数改变对损失函数的影响进行可视化。比如学习率太小（蓝色的线），损失函数下降的非常慢；学习率太大（绿色的线），损失函数下降很快，但马上就卡住不下降了；学习率特别大（黄色的线），损失函数就飞出去了；红色的就是差不多刚好，可以得到一个好的结果。

自适应学习率

举一个简单的思想：随着次数的增加，通过一些因子来减少学习率

• 通常刚开始，初始点会距离最低点比较远，所以使用大一点的学习率
• update好几次参数之后呢，比较靠近最低点了，此时减少学习率
• 比如 ${\eta }^t=\frac{{\eta }^t}{\sqrt{t+1}}$，$t$ 是次数。随着次数的增加，${\eta }^t$ 减小

学习率不能是一个值通用所有特征，不同的参数需要不同的学习率

Adagrad 算法

Adagrad 是什么？
每个参数的学习率都把它除上之前微分的均方根。解释：
普通的梯度下降为：

$$w^{t+1}\leftarrow w^t-{\eta }^t{g}^t\text{\hspace{1em}(3)}$$ $${\eta }^t=\frac{{\eta }^t}{\sqrt{t+1}}\text{\hspace{1em}(4)}$$

• $w$ 是一个参数

Adagrad 可以做的更好：
$$w^{t+1}\leftarrow w^t-\frac{{\eta }^t}{{\sigma }^t}{g}^t\text{\hspace{1em}(5)}$$ $$g^t=\frac{\partial L({\theta }^t)}{\partial w}\text{\hspace{1em}(6)}$$

• ${\sigma }^t$ :之前参数的所有微分的均方根（$root$ $mean$ $square$），对于每个参数都是不一样的。

Adagrad举例

下图是一个参数的更新过程

将 Adagrad 的式子进行化简：

Adagrad存在的矛盾

在 Adagrad 中，当梯度越大的时候，步伐应该越大，但下面分母又导致当梯度越大的时候，步伐会越小。

（1）下图是一个直观的解释：

（2）下面为一个正式的解释：

比如初始点在 $x_0$，最低点为 $-\frac{b}{2a}$，最佳的步伐就是 $x0$ 到最低点之间的距离 $\left|x_0+\frac{b}{2a}\right|$，也可以写成 $\left|\frac{2a{x}_0+b}{2a}\right|$。而刚好 $|2a{x}_0+b|$ 就是方程绝对值在 $x_0$ 这一点的微分。

这样可以认为如果算出来的微分越大，则距离最低点越远。而且最好的步伐和微分的大小成正比。所以如果踏出去的步伐和微分成正比，它可能是比较好的。

结论1-1：梯度越大，就跟最低点的距离越远。

这个结论在多个参数的时候就不一定成立了。

多参数下结论不一定成立

对比不同的参数

上图左边是两个参数的损失函数，颜色代表损失函数的值。如果只考虑参数 $w_1$，就像图中蓝色的线，得到右边上图结果；如果只考虑参数 $w_2$，就像图中绿色的线，得到右边下图的结果。确实对于 $a$ 和 $b$，结论1-1是成立的，同理 $c$ 和 $b$ 也成立。但是如果对比$a$ 和 $c$，就不成立了，$c$ 比 $a$ 大，但 $c$ 距离最低点是比较近的。

所以结论1-1是在没有考虑跨参数对比的情况下，才能成立的。所以还不完善。

之前说到的最佳距离 $\left|\frac{2a{x}_0+b}{2a}\right|$，还有个分母 $2a$ 。对function进行二次微分刚好可以得到：
$$\frac{{\partial }^{2}y}{\partial x^2}=2a\text{\hspace{1em}(7)}$$
所以最好的步伐应该是：
$$\frac{一次微分}{二次微分}$$
即不止和一次微分成正比，还和二次微分成反比。最好的step应该考虑到二次微分：

Adagrad 进一步的解释

再回到之前的 Adagrad

如上图中，比较平滑的曲线（左边）的一次微分比较小，而比较尖的（右边）的一次微分比较大.

对于 $\sqrt{{\sum }_{i=0}^t(g^i{)}^2}$ 就是希望再尽可能不增加过多运算的情况下模拟二次微分。（如果计算二次微分，在实际情况中可能会增加很多的时间消耗）

2）随机梯度下降法SGD

之前的梯度下降（又称为批量梯度下降法BGD，$Batch$ $Gradient$ $Descent$）：

$$L=\sum _n({\hat{y}}^n-(b+\sum w_i{x}_i^n){)}^2\text{\hspace{1em}(8)}$$ $${\theta }^i={\theta }^{i-1}-\eta ▽L({\theta }^{i-1})\text{\hspace{1em}(9)}$$

而随机梯度下降法SGD（$Stochastic$ $Gradient$ $Descent$）更快：

损失函数不需要处理训练集所有的数据（求所有点的梯度之和），选取一个例子 $x^n$

$$L=({\hat{y}}^n-(b+\sum w_i{x}_i^n){)}^2\text{\hspace{1em}(10)}$$ $${\theta }^i={\theta }^{i-1}-\eta ▽L^n({\theta }^{i-1})\text{\hspace{1em}(11)}$$

此时不需要像之前那样对所有的数据进行处理，只需要计算某一个例子的损失函数Ln，就可以赶紧update 梯度。

对比：

常规梯度下降法走一步要处理到所有二十个例子，但随机算法此时已经走了二十步（每处理一个例子就更新）

SGD特点：牺牲精度，降低时间复杂度。其实也可以使用BGD和SGD的折中方法——MBGD，$Mini-Bathc$ $Gradient$ $Descent$，假如有100万个数据，MBGD每次用100个或者1000个数据来更新参数（既不会太慢，也不会太随机）。MBGD更新每个Wj的公式为（其中batch_size个数据是随机选取的）：

3）特征放缩Feature Scaling

比如有个函数： $$y=b+w_1{x}_1+w_2{x}_2\text{\hspace{1em}(12)}$$ 两个输入的分布的范围很不一样，建议把他们的范围缩放，使得不同输入的范围是一样的。

为什么要这样做？

下图左边是 $x_1$ 的scale比 $x_2$ 要小很多，所以当 $w_1$ 和 $w_2$ 做同样的变化时，$w_1$ 对 $y$ 的变化影响是比较小的，$x_2$ 对 $y$ 的变化影响是比较大的（可以看出等高线的沿着w2轴平行线方向——陡坡）。

坐标系中是两个参数的error surface（现在考虑左边蓝色），因为 $w_1$ 对 $y$ 的变化影响比较小，所以 $w_1$ 对损失函数的影响比较小，$w_1$ 对损失函数有比较小的微分，所以 $w_1$ 方向上是比较平滑的。同理 $x_2$ 对 $y$ 的影响比较大，所以 $x_2$ 对损失函数的影响比较大，所以在 $x_2$ 方向有比较尖的峡谷。

上图右边是两个参数scaling比较接近，右边的绿色图就比较接近圆形。

• 对于左边的情况，上面讲过这种狭长的情形不过不用Adagrad的话是比较难处理的，两个方向上需要不同的学习率，同一组学习率会搞不定它。
• 而右边情形更新参数就会变得比较容易。左边的梯度下降并不是向着最低点方向走的，而是顺着等高线切线法线方向走的。但绿色就可以向着圆心（最低点）走，这样做参数更新也是比较有效率。

怎么做缩放？

方法非常多，这里举例一种常见的做法：

上图每一列都是一个例子，里面都有一组特征。

对每一个维度 $i$（绿色框）都计算平均数，记做 $m_i$；还要计算标准差，记做 ${\sigma }_i$。

然后用第 $r$ 个例子中的第 $i$ 个输入，减掉平均数 $m_i$，然后除以标准差 ${\sigma }_i$，得到的结果是所有的维数都是 $0$，所有的方差都是 $1$

2.梯度下降的数学理论

当用梯度下降解决问题：$${\theta }^{\ast }=\underset{\theta }{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}L(\theta )\text{\hspace{1em}(1)}$$每次更新参数 $\theta$，都得到一个新的 $\theta$，它都使得损失函数更小。即$$L({\theta }^0)>L({\theta }^1)>L({\theta }^2)>\cdot \cdot \cdot \text{\hspace{1em}(13)}$$上述结论正确吗？结论是不正确的。

比如在 ${\theta }^0$ 处，可以在一个小范围的圆圈内找到损失函数细小的 ${\theta }^1$，不断的这样去寻找。

接下来就是如果在小圆圈内快速的找到最小值？

1）泰勒展开式

定义
若 $h(x)$ 在 $x=x_0$ 点的某个领域内有无限阶导数（即无限可微分，infinitely differentiable），那么在此领域内有：

$$\begin{array}{rl}h(x)& =\sum _{k=0}^{\infty }\frac{h^k(x_0)}{k!}(x-x_0{)}^k\\ & =h(x_0)+h^{\prime }(x_0)(x-x_0)+\frac{h^{\prime \prime }(x_0)}{2!}(x-x_0{)}^2+\cdots \end{array}\text{\hspace{1em}(14)}$$

当 $x$ 很接近 $x_0$ 时，有 $h(x)\approx h(x_0)+h^{\prime }(x_0)(x-x_0)$
式14 就是函数 $h(x)$ 在 $x=x_0$ 点附近关于 $x$ 的幂函数展开式，也叫泰勒展开式。

举例：

图中3条蓝色线是把前3项作图，橙色线是 $sin(x)$。

多变量泰勒展开式

下面是两个变量的泰勒展开式

2）利用泰勒展开式化简

回到之前如何快速在圆圈内找到最小值。基于泰勒展开式，在 $(a,b)$ 点的红色圆圈范围内，可以将损失函数用泰勒展开式进行简化：

将问题进而简化为下图：

不考虑s的话，可以看出剩下的部分就是两个向量$(△{\theta }_1,△{\theta }_2)$ 和 $(u,v)$ 的内积，那怎样让它最小，就是和向量 $(u,v)$ 方向相反的向量

然后将u和v带入。

发现最后的式子就是梯度下降的式子。但这里用这种方法找到这个式子有个前提，泰勒展开式给的损失函数的估算值是要足够精确的，而这需要红色的圈圈足够小（也就是学习率足够小）来保证。所以理论上每次更新参数都想要损失函数减小的话，即保证式1-2 成立的话，就需要学习率足够足够小才可以。

所以实际中，当更新参数的时候，如果学习率没有设好，是有可能式1-2是不成立的，所以导致做梯度下降的时候，损失函数没有越来越小。

式1-2只考虑了泰勒展开式的一次项，如果考虑到二次项（比如牛顿法），在实际中不是特别好，会涉及到二次微分等，多很多的运算，性价比不好。

3.梯度下降的限制

容易陷入局部极值
还有可能卡在不是极值，但微分值是0的地方
还有可能实际中只是当微分值小于某一个数值就停下来了，但这里只是比较平缓，并不是极值点

三、Gradient Descent (Demo by AOE)

• 利用帝国时代的方式模拟梯度下降；
• 在地图上大多数位置我们是未知的，只有我们单位走过的地方是可知；
• 地图上的海拔可以看作损失函数loss function，我们的目的就是寻找海拔的最低点的值；
• 随机初始一个位置，朝向较低的方向移动，周而复始，直到local minimal(在不开天眼的情况下，你始终不会知晓所在位置是否为global minimal)。

四、Gradient Descent (Demo by Minecraft)

• 利用梯度下降法更新参数，损失函数loss function可能会不降反升(利用Mincraft解释该情况)；
• 人物的前方是较低方向，右方也是较低方向，利用梯度下降法，往右前方移动一步，然后反复用梯度下降法，往右前方移动一步，周而复始；
• 尽管前方和右方是下降的方向，但往右前方移动，将会失败(因为实际右前方是比较高的地方)。

五、Reference

datawhale笔记