您现在的位置是：主页 > news > 网站后台怎么替换图片/友情链接交换标准

网站后台怎么替换图片/友情链接交换标准

admin2025/5/23 9:15:04【news】

简介网站后台怎么替换图片,友情链接交换标准,如何让自己的网站被百度收录,做网站前台模板加推数据特征工程实战在机器学习或使用之前对数据进行清洗、标准化、降维等，是技术人员必不可少的技能?从需求说起系统用户有大量的频度指标，我们希望对用户画像进行分类和打标。(分类与聚类)?产品运营有大量的指标需要分析，产生有价值的报…

网站后台怎么替换图片,友情链接交换标准,如何让自己的网站被百度收录,做网站前台模板加推数据特征工程实战在机器学习或使用之前对数据进行清洗、标准化、降维等，是技术人员必不可少的技能?从需求说起系统用户有大量的频度指标，我们希望对用户画像进行分类和打标。(分类与聚类)?产品运营有大量的指标需要分析，产生有价值的报…

加推数据特征工程实战

在机器学习或使用之前对数据进行清洗、标准化、降维等，是技术人员必不可少的技能?

从需求说起

  • 系统用户有大量的频度指标，我们希望对用户画像进行分类和打标。(分类与聚类)?
  • 产品运营有大量的指标需要分析，产生有价值的报表。(聚类)
  • 销售膜拜、电话、大客，还是团队作战，哪项行为更符合我们的产品？(分类)?

数据科学的第一步：特征工程

  • 特征工程，说白了就是对待分析的数据进行预处理、特征选择、降维等操作。?

基础知识(主要是矩阵操作)

3cbbd5c4a1375d81b7b0ae88820bbf52.png

首先随便用JS写一套 矩阵操作的函数集(编写难度很低，看着公式，中级程序猿可以轻易完成300行代码左右)?

线代基础网上很多，我们用到的也就是这些基础的组合，上一篇卷积操作会相对难一些。

  • 复制矩阵(浅copy)
  • 矩阵转置(下面会用到)
matrix.transpose = function (arr) {
  let result = new Array(arr[0].length)
  for (let i = 0; i 0].length; i++) {
    result[i] = new Array(arr.length)
    for (let j = 0; j       result[i][j] = arr[j][i]
    }
  }
  return result
}
  • 加法
  • 减法
  • 比例
  • 叉乘
  • 点乘
  • 矩阵行列式(det)
  • 全 0 矩阵(zero)
  • 单位矩阵(I)
  • 高斯约旦消元法
  • 求逆矩阵(inv)

封装到Sky核心库的 $.math.mat 下

有了这几个基础函数我们就可以完(wei)成(suo)功(yu)能(wei)?

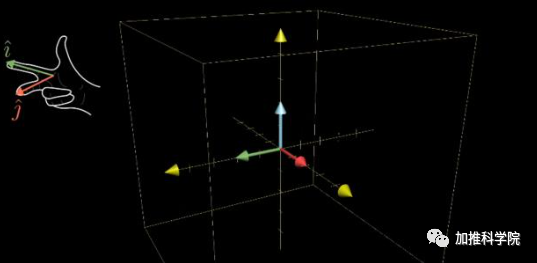
矩阵操作就是线性转换，大部分的线性变化都会改变向量的方向

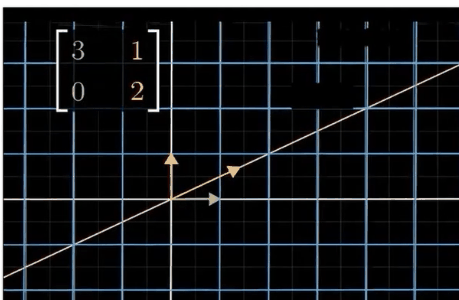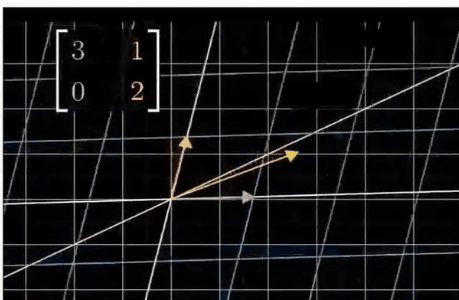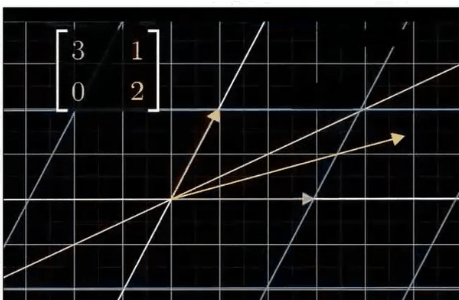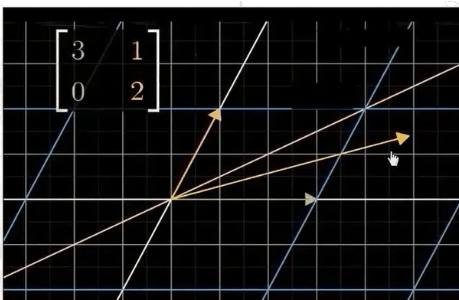
7ea6eb403a5cf7d2baaf58ec0511fe16.gif

到底有哪些有用的预处理(干货)

无量纲化

无量纲化使不同规格的数据转换到同一规格。比如把数据缩放到[0,1]区间等

1、标准化(z-score)

每个数据减去此维度(列)的平均值(mean)除以此维度的标准差或样本标准差(注意标准差和样本标准差的区别)?

2、区间缩放(归一化)

每个数据减去此维度(列)的最小值(min)除以他们的极差(range:max-min)好像很简单，常用的处理方式?

就这2个常用的，其他方法不多说，上JS代码?

let oriArr = [[1,3],[2,4],[3,5]] //3行数据2个维度 这个很重要！！ 对应矩阵的行列
let arr = $.math.mat.transpose(oriArr) // 使用矩阵转置后 [[1,2,3],[3,4,5]]
function zScoreNorm (a) {
  return a.map(x => {
    let mean = $M.mean(x)
    let std = $M.stddev(x)
    x = x.map(it => (it - mean) / std)
    return x
  })
}
function minMaxNorm (a) {
  return a.map(x => {
    let max = $M.max(x)
    let min = $M.min(x)
    x = x.map(it => (it - min) / (max - min))
    return x
  })
}

缺失值计算

  • 一般出现null 或 NaN的值，用此维度(列)的mean值填充，当然还可以按最近的填充，直接删除，拟合填入或者人工填入特定值
  • 数据量大的时候，可以直接删除?

降维

主成分分析法(PCA)我们详细说一下这个，是最常用的降维方式

举个例子就是你在3维世界，但你的影子是在平面上的，影子表征了你的特征，但它不是你?

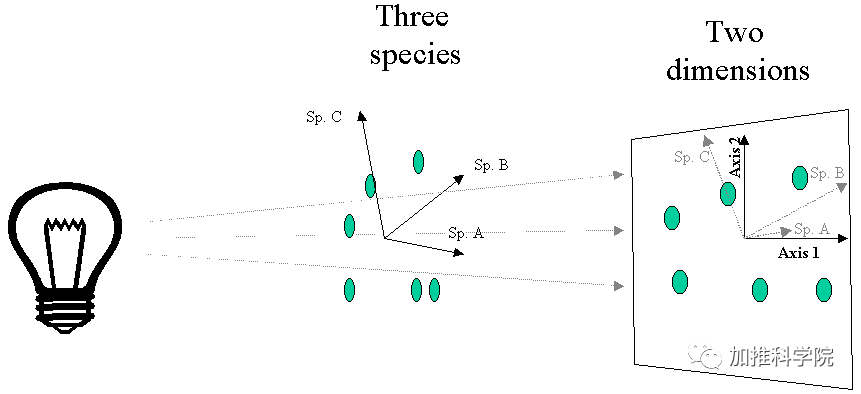
a9edbbc13d04d66b565674ce7116af6b.png

PCA算法的执行步骤

将数据每个维度，中心化(零化均值)，注意这里不是缩放，只是 减去mean

  • 每个数据减去他所在列的平均值，上代码

function meanStandard (a) {
  let meanArr = []
  // 均值中心化
  let arr = $M.mat.transpose(a).map(x => { // 注意这里是原数据矩阵的话，需要转置
    let mean = $M.mean(x)
    meanArr.push(mean)
    x = x.map(it => it - mean) // 每列减去本列的mean值
    return x
  })
  return { meanMat: $M.mat.transpose(arr), meanArr: meanArr }
}

将原始数据转置后，求出协方差，并形成矩阵

  • 方差计算应该人人都会了?

  • 样本协方差计算公式，方差是特殊的协方差X=Y $$

    协方差矩阵就是

    对于n维

    把公式写成代码?

    const cov = function (mat) {
      let len = mat.length
      let a = []
      for (let i = 0; i     a[i] = []
        for (let j = 0; j       a[i][j] = $M.covarianceCorrect(mat[i], mat[j]) / len //可以不除len,最后的数据只是影响缩放
        }
      }
      return a
    }

    将协方差矩阵进行SVD奇异值分解(方阵M*M可以特征值分解，非方阵一般使用奇异值分解

    SVD是一个O(N^3)的算法，Google有并行解决方案，最近都喜欢用GPU算，自行扩展阅读

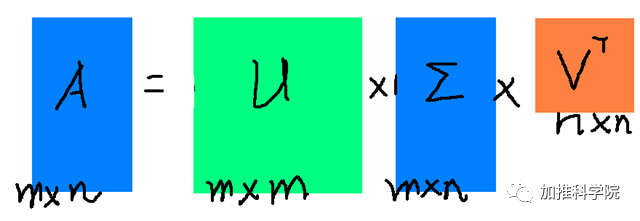
    0b5f07a6e7c88094322ad64b8411b545.png

  • 图1

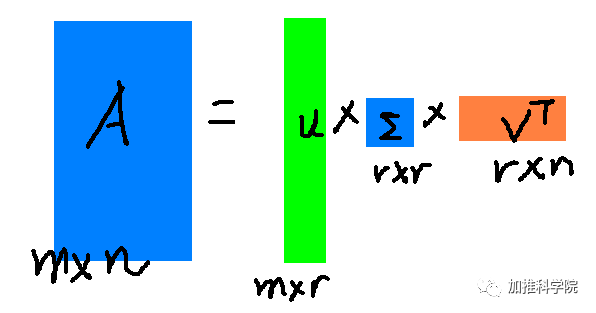
    0e8332f483b48e01516747a710cf3005.png

  • 图2

    上面第1个图，代表矩阵A，先旋转再拉伸，最后投影到V基

    上第2图R<=N，如果R被缩小，最后的数据就从 MxN => MxR，也就是被降维了

    U代表一个 正交矩阵，也就是 每个维度都是垂直的?，理解一下4个维度互相垂直的情景:cry:

    注意这里西格玛 不是累加算子? 

用findMainFactor函数，找到最佳阀值点

  • R是一个对角矩阵，对角线上的值成为奇异值(方阵的话叫特征值)

  • 也就是一串数值，没啥神奇

  • 如果我们的阀值threshold=0.95，就是需要取多少个R，让R/总奇异值和>=threshold

  • 在下面鸢尾花的例子中，取2列就可以达到97%，意味着2维新数值维度，可以很好解释原4维

  • 上代码

  • function findMainFactor (a, percent = 0.95) {
      let sum = $M.sum(a)
      let cumulat = 0
      for (let i = 0; i     cumulat += a[i]
        if (cumulat / sum >= percent) {
          return i + 1
        }
      }
      return a.length
    }

  • 非常简单?

按阀值的维度取左奇异矩阵的，相应降维后维度

降维R后，相同降维左奇异矩阵U，别急下面有代码:smile:

将中心化后的数据和上面的降维后的维度，矩阵相乘

拿出上面的矩阵乘操作

得出相应压缩过的新矩阵(降维矩阵)

于是整个过程就是一个无监督学习过程?

说了这么多公(fei)式(hua)具体怎么做(干货)？
  • 全网搜索后，发现PCA算法几乎都是Python的实现，全栈小伙伴表示不服
  • 用上面基础矩阵函数随便撸一个JS实现，4行代码搞定：
function PCA (data, threshold = 0.95, normfunc = util.none) {  
  let arr = util.cov($M.mat.transpose(data))// 求协方差矩阵
  let qMatrx = SVD(arr) // 奇异值分解
  let mainFactorLen = findMainFactor(qMatrx.q, threshold) // 自动发现最佳主因素，默认损失率<=5%对应默认95%
  let transData = $M.mat.mul(// 矩阵乘法，计算映射降维后的数据
    util.meanStandard(normfunc(data)).meanMat, // 数据中心化
    qMatrx.u.map(x => x.slice(0, mainFactorLen)) // 奇异值分解中的左奇异矩阵
  )
  return {
    mat: transData,
    mainFactorLen
  }
}
特征值(奇异值)
let r = PCA(dataIris).q //计算鸢尾花数据集的奇异值
/*
[
  1.0562101920800278,
  0.06056089290687881,
  0.019630977023538623,
  0.005920756781500258
]
*/
  • 可以看出来 前2项 占到总体的97.7%
  • 所以可以通过用2维，代替原来的4维
实例比对
使用鸢尾花数据集：

44b285115b6dd6671889a4eb136f0ccf.png

  • 鸢尾花数据集最初由Edgar Anderson 测量得到，而后在著名的统计学家和生物学家R.A Fisher于1936年发表的文章「The use of multiple measurements in taxonomic problems」中被使用
  • 鸢尾花数据集共收集了三类鸢尾花，即Setosa鸢尾花、Versicolour鸢尾花和Virginica鸢尾花，每一类鸢尾花收集了50条样本记录，共计150条:smile:，组成150*4的矩阵
  • 每条记录都有 4 项特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度
  • 在统计学习和机器学习领域都经常被用作示例

简单的说我们要对鸢尾花的4维特征数据进行降维

先上Python，科学库已经内置鸢尾花数据集，运行10万次

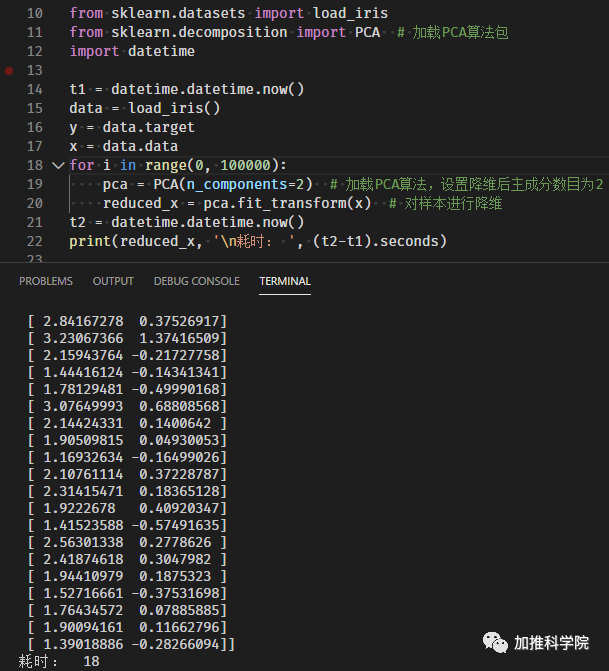
f84df6f5f1360eb9996bb2b5c52c3182.png

JS代码运行结果

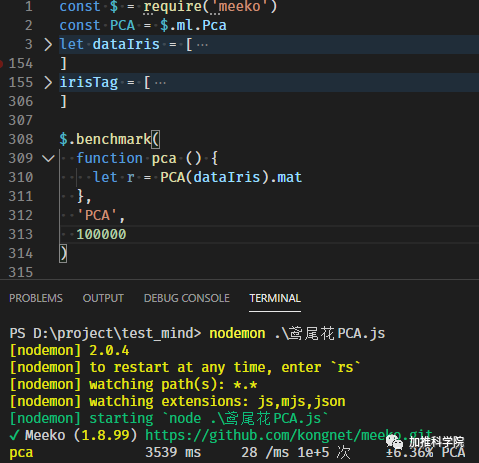
5775a80b3640a5f5083706088e049a0b.png

非常意外，JS实现比Python科学库快5倍，反复确认，操作过程相同，先PCA降维，再映射原数据集?

https://github.com/kongnet/meeko/blob/master/sample/%E9%B8%A2%E5%B0%BE%E8%8A%B1PCA.js

可视化
疑难点说明
  • python库使用n_components=2，这里是强制将4维降维2维，但一般并不知道应该降到几维
  • JS实现使用 threshold概念，即默认情况下降维压缩后的数据要保留95%的数据解释能力?
  • 网上随便找了一个python鸢尾花降维后的图像，比对本次JS实现图像：

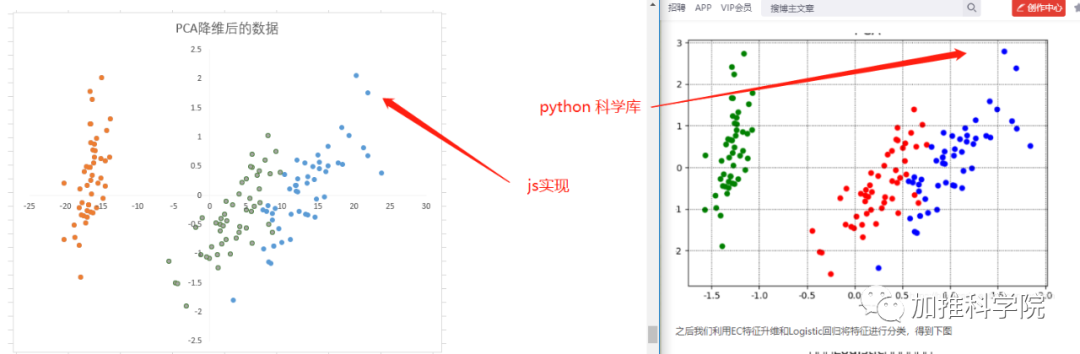
ee7741af64843731839ea73827b1a6f4.png

降维的广泛应用

  • 图片降维，我们熟知的jpeg格式，当然算法更复杂
  • 人脸识别，朋友建议先CNN选取特征值后，再用一下PCA
  • 推荐系统(找相关性)，当然这个不是降维，而是用到其中的SVD奇异值分解，思路类似
  • 销售指标，用户行为指标，运营指标的降维，这也是我们的重要应用场景
  • 特征工程之后，就可以愉快的开始机器学习的征途了?

书籍的推荐

4e331b87c2f5f61ce237b7607734d8a8.png

总结

通过对特征工程的简单介绍，用JS实现矩阵操作，进一步实现协方差矩阵，最终实现PCA降维分析全部算法，对数据科学中的数据预处理阶段有了初步了解。

祝大家2020提升技术，开心，发财 ?

相关文章

最新文章