山西手机响应式网站建设/外包公司和劳务派遣

无论时代再如何变，人类的知识体系永远不会变，除非这个世界本身就不是真实的。

很多人不喜欢数学，其实这是普遍现象，但是这个世界就是依靠数学运转着，除非你会魔法，那么你就不需要数学，从入行到现在，我依然不会觉得算法不重要，你只要打好业务代码就好了，难得就不做，这一点我是不行的，就像今天研究dns一样，找了许许多多的方案，最终决定尝试一种方案，一天下来没做啥，真的累了，数据更直观，用相应的公式和数据进行分析，这样就能做出你预期想要的答案，可能有种感觉，回到了中学（如果真能回到中学，我还真想回去，有时候感觉爱因斯坦的物质守恒定论可能并不真确，当然这只属于我个人观点，机器学习的时代的来临为我们能够节约多少时间，这是显而易见，这条路还很长，我们的路还需要慢慢摸索，加入真的有一天人工智能达到了钢铁侠中的jarvis一样，那我真的解放了，世界会怎么样，真的值得期待）。

机器世代的来领早已经开始，下一个时代将是人工智能和数据的时代，也是信息安全保卫战的时代。

信息在那个时代都不过时，我们是信息的使用者，也是信息的创造者，我们这个时代还没有将信息完全的分类和守护好，创造利益是我们当前要做的事，利益的趋向能使当前技术的成熟。

话不多说开始学习线性回归（线性回归，猛地一听是不是想起了线性回归方程，对的就是你了解的线性回归方程，这里我们说的是一元线性回归方程，不难，你会一次方程就会一元线性回归方程，这里不过只是增加了几个概念）：

一元线性回归的基本形式就是

。通过这个我们可以得到的一个结论是

。这里我们可以用这个方程代替：

,这个我想大家就认识了，通常我们是依照下面的图求出方程：

那时候们是手动求出这条直线，也就是

这个方程。而在实际中我们可以利用简单的一元一次方程进行线性回归预测。

这里我说几个概念：线性相关、协方差、相关系数、决定系数R平方，以及最小二乘法。

线性相关：

这里有几个特性：正向相关、负相关、不相关，这几个特性其实是依靠数据将这些相关性反映出来。

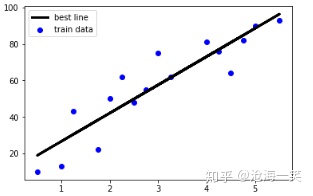
正相关：随着x轴值的增大，y增大，这就是正相关，这里我们讨论的是一次方程，要说正相关其实和系数b相关[也就是斜率],斜率为正，那就是正相关，下图就是正相关的绘制曲线：

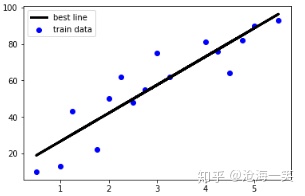
负相关与正相关相反的特性就是负相关，随着x值增大，y值减小，最主要的反应就是斜率为负，不难想象散点图的分布：

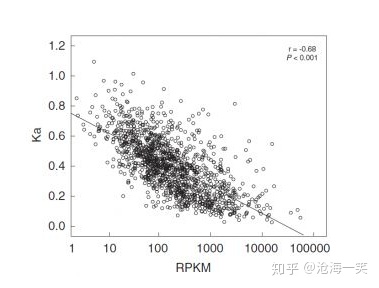
无相关（没有相关性）：这个特性就是既不是正相关，又不是负相关，两种相关性都不符合，那么就是无相关（这种说法可能也不准确，理论上说一切事物都能够用数学解释，主要是你需要寻找一种模型解释现有的数据），下图我们不能用线性方程解释：

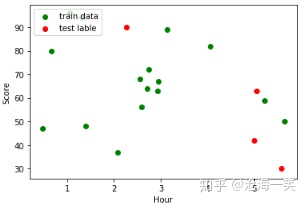
协方差（协方差主要描述变量之间的相关性）：

两个数据点的协方差(：

这里其实求得是单一的期望。

协方差也有缺点：当我们利用协方差描述相关性时，如果两个点的数据变化幅度不想同时，所求的期望差值太大，我们就不能够用协方差进行相关性描述，为此我们需要排除这样的影响，这里我们就需要利用相关系数进行相关性描述。

对于协方差的基本了解我推荐看这篇博客：

如何通俗易懂地解释「协方差」与「相关系数」的概念？ - GRAYLAMB的回答 - 知乎 https://www.zhihu.com/question/20852004/answer/134902061

相关系数：

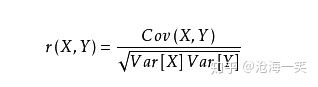
相关系数系数能够将协方差的影响剔除掉，这一点我们需要进一步学习：

这里我依然推荐刚才那篇博客：

如何通俗易懂地解释「协方差」与「相关系数」的概念？ - GRAYLAMB的回答 - 知乎 https://www.zhihu.com/question/20852004/answer/134902061

这里我们可以用一句话总结：相关系数是标准化后的协方差

相关系数有三个极值：r=-1,r=+1,r=0，r的值有不同的含义。

r=-1:负线性关

r=+1:正相关

r=0:非线性相关

相关系数值的大小表示又有分类：0-0.3表示弱相关，0.3-0.6表示中等相关程度，0.6-1表示强相关。

下面我们开始用代码来分析线性相关：

在这之前我说一下进行线性分析在模型分析中会用到的知识点：特征工程

特征工程是使用专业背景知识和技巧处理数据，使得特征能在机器学习算法上发挥更好的作用的过程。现实生活中我们我们描述一个物体物体是怎样的，那么我就需要将这个事物相应的特点描述出来，而这些特点就是我们现在说的特征。而这些特征汇集成一个事物（这里的事物可能就是现实生活中的物品，也可能就是我们的评价等等），这里的事物就是标签，这些标签相对应的就有这些特征。比如下面的猫和驴

如果我将这两张图截取：

仅凭前三张截图，我们大体就能推论出这是一只猫，这是我们固有映像得出的答案，这个答案就是标签。这里面就有相关性的问题，上面已经讲解过相关性了。

这里我们我没用用真实的数据，使用的随机生成的数据进行讲解，大部分产生的数据都是不相关的。

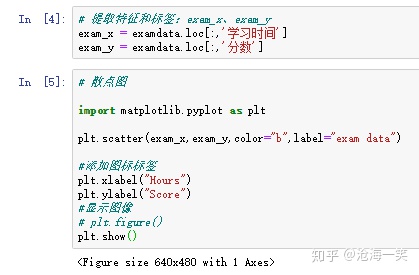
提取特征，这部分。我在我在pycharm 中执行是可以显示现实图片的，这里只是给出了对象。

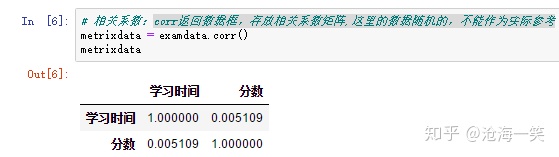
相关系数，我这里显示的相关系数是0.005109，这里如果我再刷新一次就是负数，基本是不相关的，这里不能用线性相关来解释。

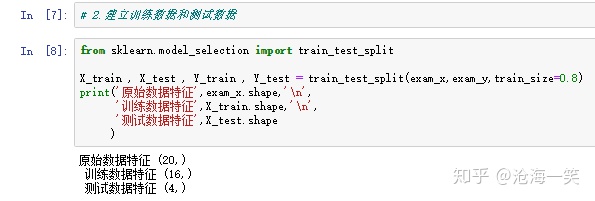
这里的测试数据占用0.2，训练数据占用0.8，这个值得规定是train_testsplit中的train_size决定的。

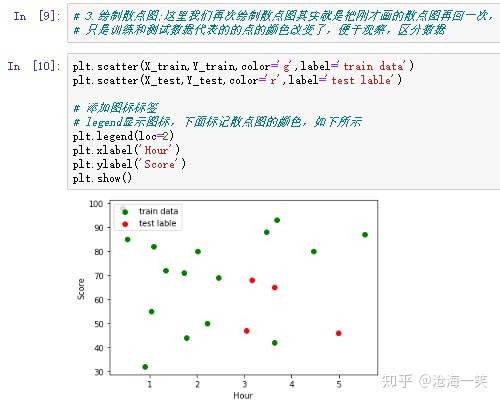
这一步只是为了展示训练数据和测试数据

训练模型，这一步我们需要将数组转换类型，如果不转换，直接操作LinearRegression()这个函数，我们会得到下面的错误：

其实解析这个错误看他的报错就行，至于怎么解开这个谜题，上面一张图片我已经给出答案。

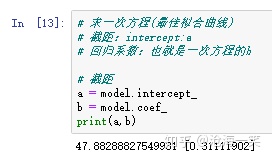
这里我们绘制直线得出的截距和回归系数这个在绘图中是用不到的

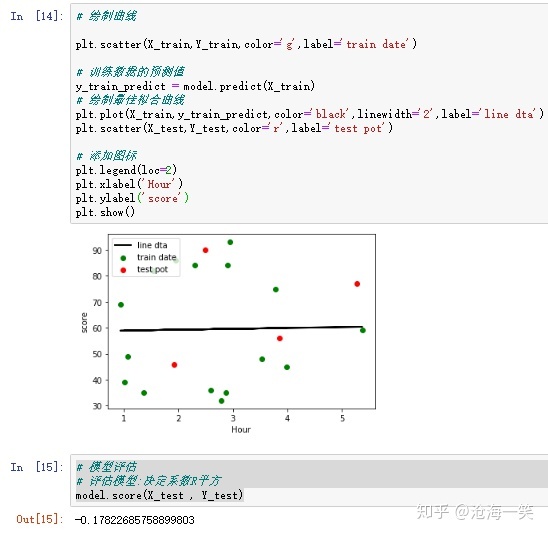
这里最后再画一次其实就是对照一下，求决定系数R平方，这里开方了，得出的结果，我想大家看懂了吧，这个数这么小，而且是负数，说明这条回归线不能描述这组数据的准确性。

好了，这次讲解，主要是对简单的线性回归属性的回顾，操作的代码很少。