ps做网站设计稿/各平台推广费用

1.利用切比雪夫不等式可以证明方差为0意味着随机变量的取值集中在一点上

2.从协方差可以得到两个变量增减的趋势，称为相关性

3.“不相关”比“独立”更弱的概念，“独立”必导致“不相关”，“不相关”不一定导致“独立”

4.相关系数是相应标准化变量的协方差，它的取值范围是[-1,1]

5.相关系数刻画了变量之间线性关系的强弱

6.协方差矩阵是一个对称的半正定(非负定)矩阵

7.协方差矩阵可以用来表示多维随机变量的概率密度(多维高斯分布上经常出现)

本篇介绍数学上最最最常用、最最最经常遇见的一些统计量。期望，方差，协方差和相关系数等。我们先从一维随机变量开始介绍。

一维随机变量

关于数学期望与方差的定义我们就直接开门见山：

离散场合数学期望

连续场合数学期望

方差与标准差

关于期望与方差的性质我们也直接给出：

在这里，我们对方差做进一步的理解，先给结论。

• 方差为0意味着随机变量的取值集中在一点上

为此，我们得先引入一个定理：切比雪夫不等式

该定理表明，大偏差发生概率的上界与方差成正比，方差越大上界也越大

利用切比雪夫不等式可以证明以下定理：

若随机变量X的方差存在，则Var(X)=0的充要条件是X几乎处处为某个常数c，即P(X=c)=1

充分性是显然的，利用方差的性质即得证。下面证明必要性：

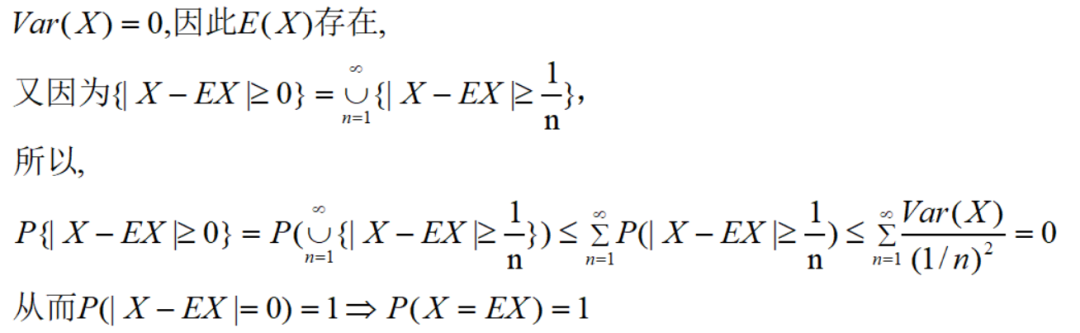
结论得证：方差为0意味着随机变量的取值集中在一点上

多维随机变量

我们给出二维随机变量数学期望的定义

n维随机变量期望与方差的性质有：

协方差与相关系数

协方差定义

协方差性质

从协方差可以得到两个变量之间的同增同减的趋势，称为相关性

• 当Cov(X,Y)>0时，称X与Y正相关：X与Y有同时增加或同时减少的倾向

• 当Cov(X,Y)<0时，称X与Y负相关：有X增加而Y减少的倾向(X减少而Y增加)

• 当Cov(X,Y)=0时，称X与Y不相关：X与Y取值毫无关联或X与Y存在其他非线性关系

这里需要提一点的是，“不相关”比“独立”更弱的概念，即“独立”必导致“不相关”，而“不相关”不一定导致“独立”

相关系数

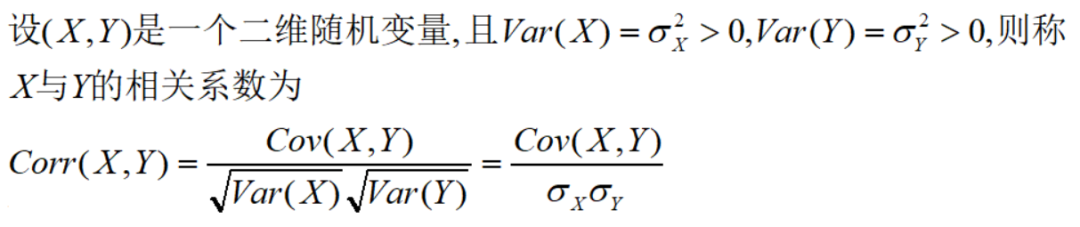
相关系数是为了消除不同变量量纲的影响而构造衡量变量相关性的另一个指标，它的本质是：相应标准化(均值为0，方差为1)变量的协方差

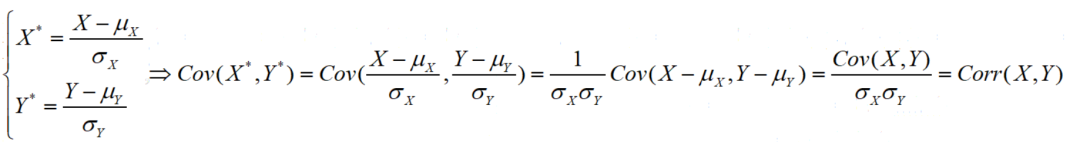
相关系数处于[-1,1]之间，具备如下性质：

1.相关系数Corr(X,Y)刻画X与Y之间的线性关系强弱

2.若Corr(X,Y)=0,则称X与Y不相关，表明它们没有线性相关关系，但可能有其他非线性关系

3.若Corr(X,Y)=1,则称X与Y完全正相关；若Corr(X,Y)=-1,则称X与Y完全负相关

4.若0

协方差矩阵

记n维随机向量X=(X1,X2,...,Xn)，若其每个分量的数学期望都存在，称矩阵

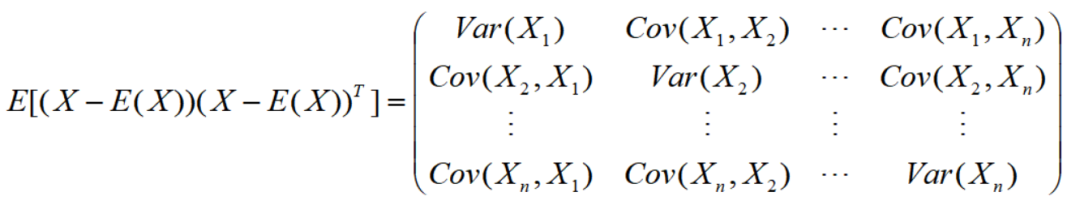
为随机向量X的协方差矩阵，记为Cov(X)

协方差矩阵是研究各种复杂模型很重要的工具，我们需要熟悉它。

通常情况下，给定n维数据m个样本的矩阵X，可以用行向量和列向量表示：

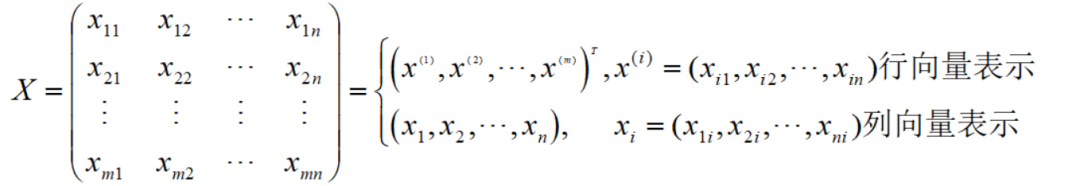
若每一维的均值为0，则矩阵X的协方差矩阵的m倍可表示为X的转置乘以X：

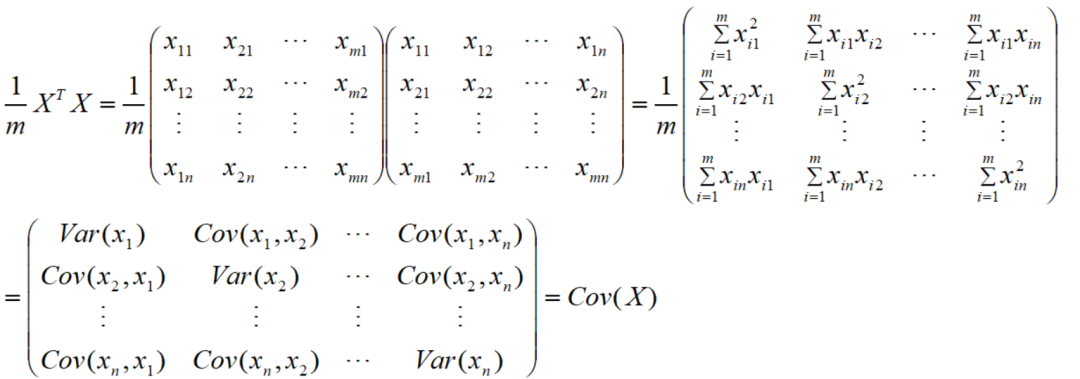
这种表示形式需要熟悉，在PCA降维，奇异值分解经常会用到，且可以用来表示多维随机变量的概率密度(这一点在高斯分布专场会专门讲解)，这里想强调一点的是，协方差必须熟悉掌握。

最后，我们介绍协方差矩阵一个重要的性质：

• 协方差矩阵是一个对称的半正定(非负定)矩阵

下面我们证明这一点：

对称性显然成立，只需证明非负性

因此，协方差矩阵是一个半正定矩阵