站长工具seo综合查询columbu cat/免费外贸接单平台

Floyd算法    

    Floyd是解决图中任意两点间最短距离的一种算法，可以处理有向图或有向带负权图(不可出现负权回路)的最短路径

算法思路：

在存在图G=(V,E)中求最短路径时，引入两个矩阵A与矩阵B，其中a[i][j]表示顶点 i 到顶点 j 的最短距离，b[i][j]表示 i 到 j 的最短路径需要经过的点，即点 i 通过 b[i][j] 到达点 j 的路径最短

• G=(V,E)是通常的图表示方法，G表示整个图，V表示点集合，E代表边集合

采用动态规划的思维方式，得到状态转移方程

    a[i][j] = min(a[i][k]+a[j][k]) k∈{x|x∈V}

我们只需要将i和j分别从点1到点n一次算出来，就可求到整个图每个点之间的最短距离，伪代码为

for (i = 1; i ∈ V; i++){  for(j = 1; j∈V j++ ) {    dis = 0x7ffffff;    for (k = 1 ; k∈V ; k++)      dis = min(dis, a[i][k]+a[k][j])    a[i][j] = dis;  }}

此算法是基础最短路径中最简便的一个算法，缺点是时间负责度较高，为

O(N³)，一般实际操作中不使用此算法，但是可以作为理解动态规划思想的基础算法

SPFA算法

    前文提到过，Dijkstra算法是通过加入最短边的方式，逐渐刷新源点到目标点的距离，SPFA也是用的类似的方法，Dijkstra是通过最短边去刷新其他的边，而SPFA则是通过点所连接的所有边去刷新其他连接点的路径。

    算法思想：

    SPFA主要采用的是动态逼近的策略。采用一个先进先出的队列R来保存所有保存待优化的点，从其中任意一点a出发，若与a相连边的另一点b，通过a出发到b点的距离，比其他路径到b的距离短，则b的路径可以更新，同时将b加入队列尾。因为b的路径更新了，相应的通过b到其他点的距离也应该更新。重复步骤，直至队列里面的数为空为止

具体步骤

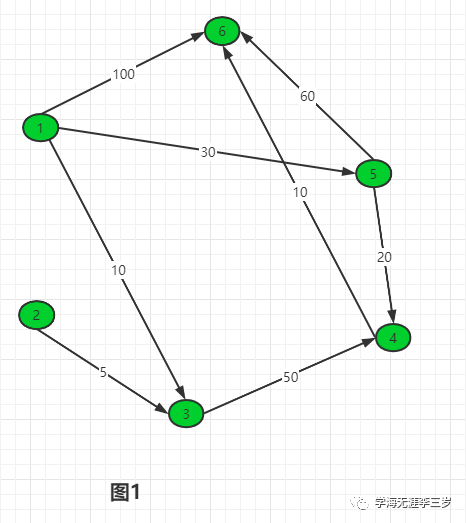
仍然以图1为例，数组S保存从源点a到 其他点的距离

初始状态下，有如下示例

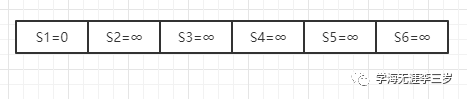
    此时R = {1}

第一次修正，通过队列R中点1点开始进行数组其他值的修正，发现点3,5,6与点1相连，且从1出发到3，5，6，的距离比数组S中的值小，于是修正3，5，6的值且把点3，5，6加入R得到

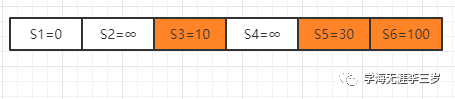
此时R = {3，5，6}

第二次修正，继续处理R中的点，通过点3得到可以修正的点4，同时把4加入R得到

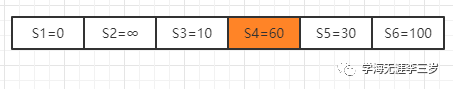
R = {5，6，4}

第三次修正，通过R中的点5，得到可以修正的点4和点6，但是因为点4和点6已经再R中，不再加入，得到

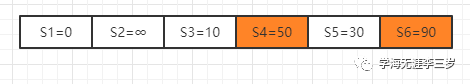
R = {6，4}

第四次修正，通过点6，得到通过6没有通向其他点的路径，不做处理，得到

R = {4}

第五次修正，通过点4，得到可以修正的点6，同时将点6加入R中，得到

R = {6}

第六次修正，结果和第四次修正一样，不做处理，得到R = {}

此时R队列处理完毕，SPFA的算法也完成，可以见到，最终的结果与前文Dijkstra的结果一致

SFPA算法由于Dijkstra算法的点就是可以包括负权边(不能出现负环)，算法实现简单，缺点是时间复杂度比较高，为O(VE)。但算法可以进行若干优化，提高了效率