您现在的位置是:主页 > news > 太原网站优化/百度免费推广平台
太原网站优化/百度免费推广平台
![]() admin2025/5/14 15:24:51【news】
admin2025/5/14 15:24:51【news】
简介太原网站优化,百度免费推广平台,外包网页制作页面多少钱一张,dedecms5.7 整个网站 css和js代码怎么优化描述 在物质位面“现实”中,有n1个星球,分别为星球0,星球1,……,星球n。 每一个星球都有一个传送门,通过传送门可以直接到达目标星球而不经过其他的星球。 不过传送门有两个缺点。 第一,从星球i…
太原网站优化,百度免费推广平台,外包网页制作页面多少钱一张,dedecms5.7 整个网站 css和js代码怎么优化描述 在物质位面“现实”中,有n1个星球,分别为星球0,星球1,……,星球n。 每一个星球都有一个传送门,通过传送门可以直接到达目标星球而不经过其他的星球。 不过传送门有两个缺点。 第一,从星球i…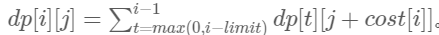
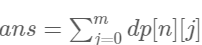
描述
在物质位面“现实”中,有n+1个星球,分别为星球0,星球1,……,星球n。
每一个星球都有一个传送门,通过传送门可以直接到达目标星球而不经过其他的星球。
不过传送门有两个缺点。
第一,从星球i通过传送门只能到达编号比i大,且与i的差不超过limit的星球。
第二,通过传送门到达星球j,需要cost[j]个金币。
现在,流浪剑客斯温到达星球0后身上有m个金币,请问他有多少种方法通过传送门到达星球n?
- 1 <= n <= 50, 0 <= m <= 100, 1 <= limit <= 50, 0 <= cost[i] <= 100。
- 由于cost[0]没有意义,题目保证cost[0] = 0。
在线评测地址:
LintCode 领扣样例1
比如 n = 15, 返回一个字符串数组:
输入:
n = 1
m = 1,
limit = 1
cost = [0, 1]
输出:
1
解释:
方案1:星球0→星球1 样例2
输入:
n = 1
m = 1
limit = 1
cost = [0,2]
输出:
0
解释:
无合法方案 算法:dp
我们用dp[i][j]dp[i][j]代表从星球00出发到达星球ii后拥有jj个金币的方案数。
- 设置初始状态为在第0号星球,此时拥有m个币。dp[0][m]=1dp[0][m]=1。
- 我们考虑dp[i][j]dp[i][j]的前继状态,可以发现,所有编号比i小,且差在limit之内的都能转移过来,并且转移过程消耗cost[i]cost[i]的币,所以对它的前继状态的方案数累加。
- 可列出状态转移方程如下所示,
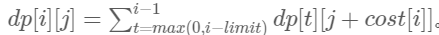
- 最后因为要求总方案数,对于sven在第nn号星球的所有剩余金币数量求和即可。答案
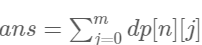
复杂度分析
- 时间复杂度O(n∗m∗limit)O(n∗m∗limit)
- 空间复杂度O(n∗m)O(n∗m)
- 就是dpi所有的状态数
public class Solution { /**
* @param n: the max identifier of planet.
* @param m: gold coins that Sven has.
* @param limit: the max difference.
* @param cost: the number of gold coins that reaching the planet j through the portal costs.
* @return: return the number of ways he can reach the planet n through the portal.
*/ public long getNumberOfWays(int n, int m, int limit, int[] cost) { //
long[][] dp = new long[n + 1][m + 1]; for (int i = 0; i < m; i++) { dp[0][i] = 0; } dp[0][m] = 1; for (int i = 1; i <= n; i++) { for (int j = 0; j <= m; j++) { dp[i][j] = 0; for (int t = Math.max(0, i - limit); t <= i - 1; t++) { if (j + cost[i] <= m) { dp[i][j] += dp[t][j + cost[i]]; } } } } long ans = 0; for (int i = 0; i <= m; i++) { ans += dp[n][i]; } return ans; }
} 更多题解参考:九章算法








