您现在的位置是：主页 > news > 企业网站建设最新技术/网站推广方式有哪些

企业网站建设最新技术/网站推广方式有哪些

admin2025/5/13 16:33:54【news】

简介企业网站建设最新技术,网站推广方式有哪些,做美食网站有哪些,大学生网站建设日程表概念 Tries树，又称键树，字典树或查找树。用来存储字符串的一种树形结构。它有三个基本性质：1 根节点不包含字符，除根节点外每一个节点都只包含一个字符。2 从根节点到某个一个节点，路径上经过的字符连接起来&#xff0…

企业网站建设最新技术,网站推广方式有哪些,做美食网站有哪些,大学生网站建设日程表概念 Tries树，又称键树，字典树或查找树。用来存储字符串的一种树形结构。它有三个基本性质：1 根节点不包含字符，除根节点外每一个节点都只包含一个字符。2 从根节点到某个一个节点，路径上经过的字符连接起来&#xff0…

概念

Tries树，又称键树，字典树或查找树。用来存储字符串的一种树形结构。它有三个基本性质：

1 根节点不包含字符，除根节点外每一个节点都只包含一个字符。

2 从根节点到某个一个节点，路径上经过的字符连接起来，为该节点对应的字符串。

3 每个节点的子节点包含的字符都不相同。

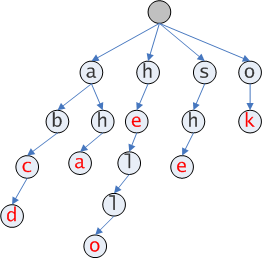
假设，我们有这些单词，hello, he, she, abc, aha, ok, abcd，对其构造字典树如下：

红色节点表示以该节点表示字符结尾的单词存在。假设我们有上面一棵字典树，现在要查找其中是否存在hell，查找过程是这样的，从根节点出发，顺序经过h-->e-->l-->l，到达l节点，因为l没有标记为红色，所以hell单词不存在。插入过程很类似于查找过程，找不到就插入。所以字典树是边查找边插入（构造）的。从图我们还可以看到具有相同前缀的单词共用相同节点。

优点

字典树是一种简单实用的结构，利用后缀树来存储字符串，可以满足多种快速查询，并相对要节约空间。

应用

用于统计单词的频率，用于快速查找。比如字典查询、单词的自动补全和自动提示就可以使用类似的结构。

有这样一个题目：给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，求第一次出现在第几个位置。

对于类似的应用，我们可以使用map来做，也就是使用二叉搜索树，树的每个节点是一个单词。当我们要查询某个单词是否出现过时，要从根节点开始进行比较，这样的比较是字符串的比较。而字典树的每个节点是一个字符，查询过程的时间复杂度为单词长度。显然查找树的效率和空间利用率都要好的多。

另外一些应用字典树解决的问题：

1 有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。

2 1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。请怎么设计和实现？

3 一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析。

实现

实现方式有多种，下面是其中一种，用如下结构表示节点

class Node {
public:Node():child(NULL), sibling(NULL), isEnd(false) {}char ch;Node *child;Node *sibling;bool isEnd;
};

/*判断p的子节点中是否含有字符ch，是则返回响应的节点，否则返回NULL
*/
Node* isChild(Node *p, char ch)
{Node *q = p->child;while (q ){if (q ->ch == ch)return q ;q = q ->sibling;}return NULL ;
}

插入操作

/*已经存在，则返回false
*/
bool Insert(Node &root, const char *s)
{Node *p=&root, *t;while(p && *s){t = isChild(p , *s);if (t == NULL)break;p = t ; s++;}if (*s == 0)return false;while(*s){Node *t = new Node;t->ch = *s;t->sibling = p ->child;p->child = t ; p = t ;s++;}p->isEnd = true; //标记终点return true;
}

查询操作

/*在数root中查找s，如果s是root的子串，则返回NULL，否则返回查找结束的节点
*/
Node* Search(Node &root, const char *s)
{Node *p=&root, *t;while(p && *s){t = isChild(p , *s);if (t == NULL)break;p = t ; s++;}if (*s==0)return NULL;elsereturn p;
}

Java版的实现

class Node {public Node() {child = null;sibling = null;}char ch;Node child;Node sibling;boolean isEnd;}/*判断p的子节点中是否含有字符ch，是则返回响应的节点，否则返回NULL*/private Node isChild(Node p, char ch){Node q = p.child;while (q != null){if (q.ch == ch)return q ;q = q.sibling;}return null ;}/*
在数root中查找s，如果s是root的子串，则返回NULL，否则返回查找结束的节点*/Node Search(Node root, String s){Node p=root, t;int i=0;while(p!=null && i<s.length()){t = isChild(p , s.charAt(i));if (t == null)break;p = t ; i++;}if (i == s.length())return null;elsereturn p;}/*
已经存在，则返回false*/boolean Insert(Node root, String s){Node p=root, t;int i=0;while(p != null && i<s.length()){			t = isChild(p , s.charAt(i));if (t == null)break;p = t ; i++;}if (i == s.length())return false;while(i<s.length()){t = new Node();t.ch = s.charAt(i);t.sibling = p.child;p.child = t ; p = t ;i++;}p.isEnd = true; //标记终点return true;}