怎么构建一个网站/网络营销的方式都有哪些

前文推导了(线性)SVM的对偶问题(见支持向量机原理详解(二): 拉格朗日对偶函数，SVM的对偶问题)。不过，线性SVM以超平面来划分两类数据，如果数据本身是非线性的，那么以超平面作为决策边界就显得不太适用了。通过引入核函数，可以使SVM适用于非线性分类问题。本文介绍核方法在SVM中的应用，以及引入核函数后的SVM对偶问题。

6. 非线性SVM

关于核函数和核技巧，已在之前'Kernel PCA'一文中做了介绍，供参考：

数据降维: 核主成分分析(Kernel PCA)原理解析

SVM中的核技巧也是类似的，大致思路是：

1. 对于
   维输入空间(input space)的数据集，通过一个(非线性)映射
   ，将其映射到
   维特征空间(feature space)；在这个更高维的特征空间，容易实现数据的线性可分；
2. 然后，在特征空间中用高维的数据求解线性SVM，得到最优分离超平面，也就得到了分类决策函数；
3. 对于新数据，先将其映射到特征空间，然后用特征空间中的分类决策函数来进行分类。

那么引入映射

后，SVM形成的优化问题是什么样的呢？

线性SVM的原问题为：

将样本

映射到特征空间得到

，由于我们并不显式地定义映射

，所以直接在原问题

中将

替换为

似乎不太方便求解。

下面来看线性SVM的对偶问题：

其中，矩阵

的

行

列的元素为

。

对偶问题

中，样本

仅出现在目标函数的矩阵

中，且矩阵

的元素为样本之间的点积。如果将

映射为

，相应的对偶问题只需对矩阵

做调整：

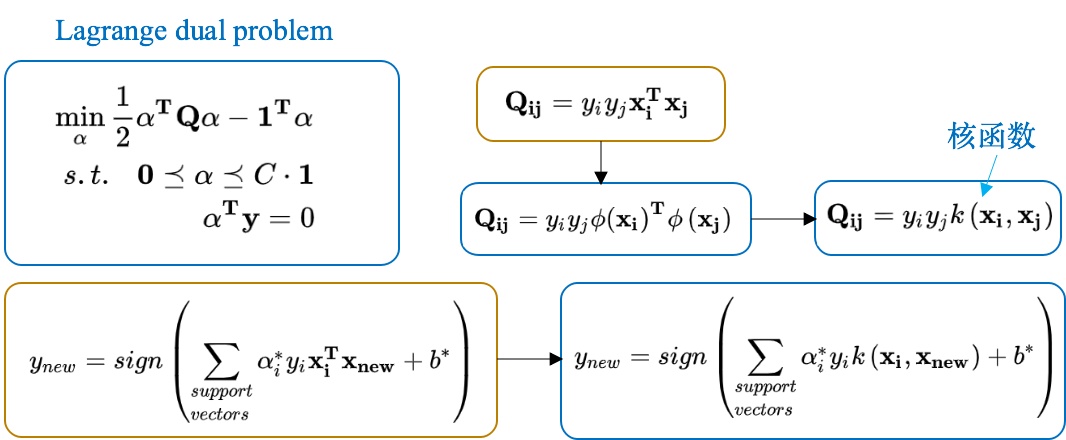
这表明可以通过对偶问题来引入核函数。

定义核函数

，用输入空间中的向量来计算特征空间中高维向量的点积，则特征空间中，

所以，引入核函数的非线性SVM的对偶问题如下：

其中，

。

若核函数

为正定核，则对偶问题

是凸二次规划问题(参考文献[3], page 124)。解之得到最优拉格朗日乘子向量

。

<分类决策函数 & 决策边界>

回忆在线性SVM中，由对偶问题

得到原问题

的最优解为

(

后续再推导。)

分类决策函数为

类似地，特征空间中由线性SVM得到的最优分离超平面的法向量为

这里

是

维向量。当然，

是无法(也不需要)显式计算的，因为分类决策函数中的向量点积由核函数计算：

在线性SVM中，决策边界是一个超平面：

而在非线性SVM中，决策边界在特征空间中是超平面，对应于输入空间中的一个超曲面：

即

解对偶问题

，得到最优拉格朗日乘子向量

，就得到了(1)式的决策函数，用于对新数据的分类。

To be continued...

参考文献

[1] C. Cortes and V. Vapnik. Support-Vector Networks. Machine Learning, 20:273–297, 1995.

[2] Christopher J. C. Burges. A Tutorial on Support Vector Machines for Pattern Recognition. Data Mining and Knowledge Discovery, 2, 121-167, 1998.

[3] 李航，统计学习方法，清华大学出版社，北京，2012年。第7章。