您现在的位置是:主页 > news > 建一个商城型网站/网络营销教学大纲
建一个商城型网站/网络营销教学大纲
![]() admin2025/5/11 4:41:51【news】
admin2025/5/11 4:41:51【news】
简介建一个商城型网站,网络营销教学大纲,wordpress音乐下载,医疗器械网站备案前置审批事例有限多和无限多Hypothesis优劣势对比 当hypothesis数量有限的时候(如下图small M),我们可以较为轻易的实现Ein(g)≈Eout(g)Ein(g)≈Eout(g),但是却有一个弊端,那就是我们的选择太有限,不能保证能够找到足够…
有限多和无限多Hypothesis优劣势对比
当hypothesis数量有限的时候(如下图small M),我们可以较为轻易的实现Ein(g)≈Eout(g)Ein(g)≈Eout(g),但是却有一个弊端,那就是我们的选择太有限,不能保证能够找到足够好的g。
当hypothesis数量无限的时候(如下图large M),我们会有更大的选择空间,能够保证我们找到相对较好的g,但是我们犯错Ein(g)≠Eout(g)Ein(g)≠Eout(g)的几率也变得更大了

虽然无限多个M可以让我们有更大的选择余地,但是这无疑增加了我们的计算难度,所以我们要想办法解决这个问题。
化无限为有限
既然无限多个M对我们的计算不利,那么有没有一种办法可以把无限的M变为有限的呢?答案是肯定的!接下来我们要做如下变换:
P[|Ein(g)−Eout(g)|>ϵ]≤2⋅M⋅exp(−2ϵ2N)⇒P[|Ein(g)−Eout(g)|>ϵ]≤2⋅mH⋅exp(−2ϵ2N)P[|Ein(g)−Eout(g)|>ϵ]≤2⋅M⋅exp(−2ϵ2N)⇒P[|Ein(g)−Eout(g)|>ϵ]≤2⋅mH⋅exp(−2ϵ2N)
还记得我们在第17节推导公式
P[|Ein(g)−Eout(g)|>ϵ]≤2⋅M⋅exp(−2ϵ2N)P[|Ein(g)−Eout(g)|>ϵ]≤2⋅M⋅exp(−2ϵ2N)的过程吗?
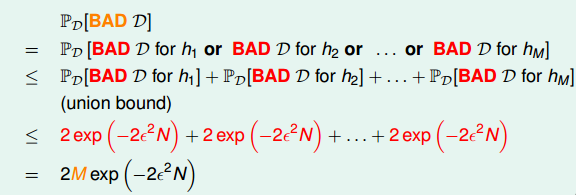
如上图,当时我们用了连集加法的形式推导,但是我们忽略了一个问题,那就是每一个BAD概率之间的重叠问题,表现如下:
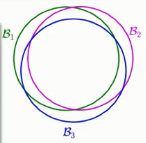
那么我们是否可以以此作为切入点,想办法把无限的M转为有限的M。答案也是肯定的,让我们继续往下看吧。
对hypothesis进行归类
要找到重叠的hypothesis,我们可以把所有的hypothesis先进行归类。我们知道,我们用于训练的数据是有限的,那么可以简单讨论以下几种情况:
只有一条数据的时候
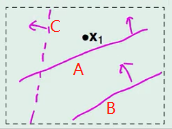
如下图,只有两种不同的分类,X1X1对于A和B箭头所指的方向表示圈圈+1,但对于C则表示叉叉-1。
有两条数据的时候
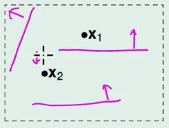
如下图,有四种不同的分类,具体如下图:
- 有三条数据的时候
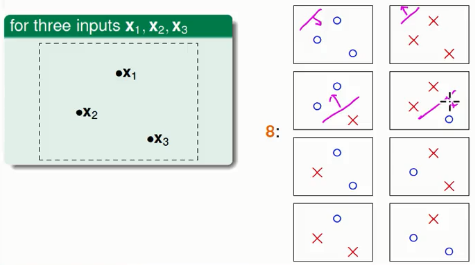
这种情况就相对比较复杂一点,当三条数据不在同一条直线上的时候,我们可以分成8种类别:
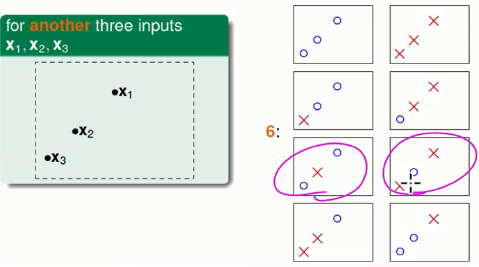
如果在同一条直线上,那么只会有6种不同的分类,如下图,被圈起来的两种分类我们是无法实现的。
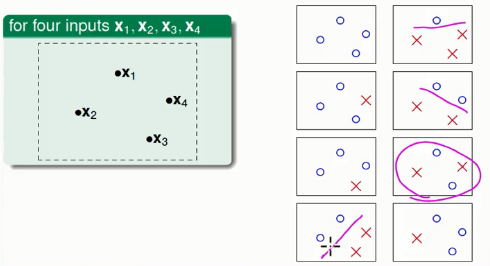
- 有四条数据的时候
这里有几种情况,比如四条数据在同一条直线上,或者出现数据重叠的情况等。现在我们只讨论四条数据不在同一条直线上的时候,可以产生14种分类,其中圈起来的那种分类我们无法实现,其他的都可以。因为图中每种分类方法又有一个对称面,所以有2×7=142×7=14种分类。
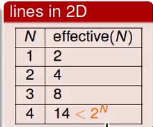
通过观察我们发现有效的线一般小于2N2N,即:
有效的线的数量(effective number of line)
我们通过上面的观察我们发现,一般情况下有效的分类线会小于M,所以现在我们可以做出一个重要的式子变换,用effective(N)来代替M,即:
P[|Ein(g)−Eout(g)|>ϵ]≤2⋅M⋅exp(−2ϵ2N)⇒P[|Ein(g)−Eout(g)|>ϵ]≤2⋅effective(N)⋅exp(−2ϵ2N)P[|Ein(g)−Eout(g)|>ϵ]≤2⋅M⋅exp(−2ϵ2N)⇒P[|Ein(g)−Eout(g)|>ϵ]≤2⋅effective(N)⋅exp(−2ϵ2N)
又因为 effective(N)<2Neffective(N)<2N,
所以当N足够大的时候2⋅effective(N)⋅exp(−2ϵ2N)2⋅effective(N)⋅exp(−2ϵ2N)会接近0.
这时候就说明P[|Ein(g)−Eout(g)|>ϵ]P[|Ein(g)−Eout(g)|>ϵ]发生坏事的几率会很低,说明我们找到了一条很合适的线g,机器学习成功了。
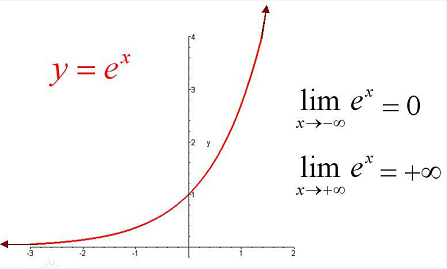
这里要复习一下exp(X)函数,该函数是以e为底的指数函数,以下是该函数的性质图,X越小,越接近于0.
上面的内容都只是我们的猜想,我们还需要进一步做严谨的证明,下一节课继续!好困啊…
===========================懵逼分割线===========================
欢迎大家加入Q群讨论:463255841
===========================懵逼分割线===========================