织梦个人网站模板/软件推广方案经典范文

斐波那契数列(Fibonacci sequence)，又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入，故又称为“兔子数列”。

斐波那契数列指的是这样一个数列：

1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 

在数学上，斐波那契数列以如下被以递推的方法定义：

F(1)=1，

F(2)=1,

 F(n)=F(n - 1)+F(n - 2)(n ≥ 3，n ∈ N*)

在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从 1963 年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

斐波那契数列数学上可以获得通项公式：

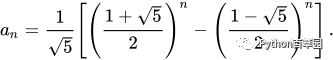
有趣的是，这样一个完全是自然数的数列，通项公式却是用无理数来表达的。而且当 n  趋向于无穷大时，前一项与后一项的比值越来越逼近黄金分割0.618(或者说后一项与前一项的比值小数部分越来越逼近 0.618)。

在计算机中，尤其是在Python中，因会引入浮点数，一般不用这个方法，而广泛使用递推公式实现。

n = int(input())       # int函数将input()接收到的字符串转成整数a,b = 1,1              # 设定初始的前2项为1和1for i in range(n):    print(a, end=' ')  # 输出当前项，不换行    a,b = b,a+b        # a + b为产生的新项，与b一起构成新的前2项print()                # 换行# 20# 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 6765

可以写成函数

def fib(n):              '''输出斐波那契数的前n项，首项从1开始'''    a,b = 1,1              # 设定初始的前2项为1和1    for i in range(n):        print(a, end=' ')  # 输出当前项        a,b = b,a+b        # a + b为产生的新项，与b一起构成新的前2项    print()                # 换行if __name__ == '__main__':    n = int(input())       # int函数将input()接收到的字符串转成整数    fib(n)                 # 调用fib()函数进行计算

可以用列表推导式方便 的获得斐波那契数列，可利用索引方法获取其中任一个数，或用ls[-1]获得最后一个数字。

n = int(input())  #int函数将input()接收到的字符串转成整数ls = [1, 1]              # 设定初始的前2项为1和1[ls.append(ls[i - 2] + ls[i - 1]) for i in range(2,n)]print(ls)# 20# [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765]

斐波那契数列特性

平方与前后项

从第二项开始，每个偶数项的平方都比前后两项之积多1，每个奇数项的平方都比前后两项之积少1。

如：第二项 1 的平方比它的前一项 1 和它的后一项 2 的积 2 少 1，第三项 2 的平方比它的前一项 1 和它的后一项 3 的积 3 多 1。

[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765]

(注：奇数项和偶数项是指项数的奇偶，而并不是指数列的数字本身的奇偶)

奇数项求和

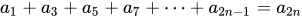
偶数项求和

ls = [1, 1]              # 设定初始的前2项为1和1[ls.append(ls[i - 2] + ls[i - 1]) for i in range(2,20)]print(ls)print(sum(ls[0:20:2]))   # 6765  奇数项和print(sum(ls[1:20:2]))   # 10945 = 4181 + 6765 - 1  偶数项和# [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765]

平方求和

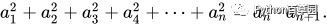
ls = [1, 1]                               # 设定初始的前2项为1和1[ls.append(ls[i - 2] + ls[i - 1]) for i in range(2,20)]print(ls)print(sum(ls[i] **2 for i in range(20)))  # 74049690print(ls[19] * (ls[19] +  ls[18]))        # 74049690