网站注入木马/网页开发教程

原文链接https://www.cnblogs.com/zhouzhendong/p/Balanced-Binary-Tree.html

注意是简单教程，不是入门教程。

splay

1. 旋转：

假设点 y 原是点 x 的 father，旋转操作可以在不改变中序遍历的基础上，将 y 变成 x 的儿子。例如：

 

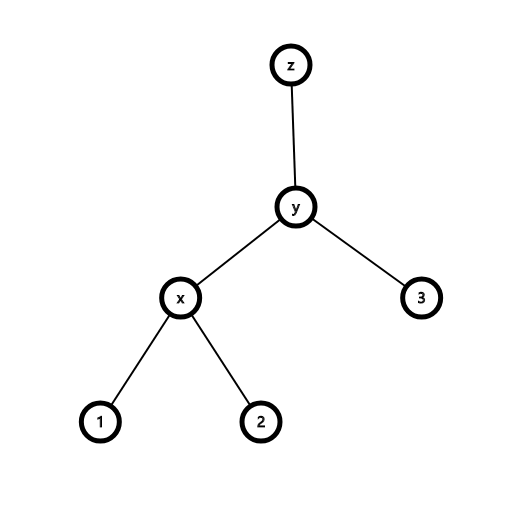
旋转后：

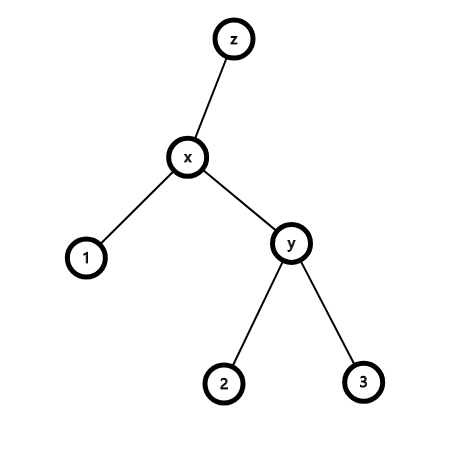
代码：

int wson(int x){return son[fa[x]][1]==x;
}
void pushup(int x){tot[x]=cnt[x]+tot[son[x][0]]+tot[son[x][1]];
}
void rotate(int x){if (!x)return;int y=fa[x],z=fa[y],L=wson(x),R=L^1;if (z)son[z][wson(y)]=x;fa[x]=z,fa[y]=x,fa[son[x][R]]=y;son[y][L]=son[x][R],son[x][R]=y;pushup(y),pushup(x);
}

 

2. splay

可以将一个点旋转到他的一个祖先下面，或者旋转到根的位置。

具体操作：

设当前旋转的点是 x ，y = fa[x] , z = fa[y] 。设 wson(x) 表示节点 x 是他的父亲的左儿子还是右儿子。

如果 wson(x) = wson(y) ，那么先旋 y，再旋 x；

如果 wson(x) $\neq$ wson(y) ,那么先选 x，再旋 x。

单次复杂度均摊 $O(\log n)$ 。

如果每次都旋转 x 的话是可以被卡掉的。

关于 splay 时间复杂度的证明：

https://www.cnblogs.com/zhouzhendong/p/JunTanFenXi.html

反正可以用就行了。注意用法是每找一个点都要 splay ，不管是插入节点还是查找特定值在平衡树中的位置。

代码：

void splay(int x,int k){if (!x)return;if (!k)root=x;for (int y=fa[x];fa[x]!=k;rotate(x),y=fa[x])if (fa[y]!=k)rotate(wson(x)==wson(y)?y:x);
}

3.插入

假设插入的值是 v。找到比 v 小的最大点，把它splay到根，找到它的右子树的最小值的位置，把新节点插到这个节点的左子节点位置即可。

4.删除

找到节点，splay到根，找到它的右子树的最左点，splay到根下面，这样就保证了根的右儿子没有左儿子，直接把根ban掉，把根左儿子变成右儿子的左儿子就好了。

5.其他

诸如查排名、查第k大、查前驱后继等比较简单，这里省略了。

关于区间修改：

可以支持翻转、区间覆盖、区间乘等等操作。

具体一些的方法是：打懒标记，每次splay之前先往上走一遍预先下传好标记，再splay。

6.模板 (BZOJ3224)

#include <bits/stdc++.h>
using namespace std;
const int N=100005;
int n,root=1,size=1,val[N],cnt[N],son[N][2],fa[N],tot[N];
int wson(int x){return son[fa[x]][1]==x;
}
void pushup(int x){tot[x]=cnt[x]+tot[son[x][0]]+tot[son[x][1]];
}
void rotate(int x){if (!x)return;int y=fa[x],z=fa[y],L=wson(x),R=L^1;if (z)son[z][wson(y)]=x;fa[x]=z,fa[y]=x,fa[son[x][R]]=y;son[y][L]=son[x][R],son[x][R]=y;pushup(y),pushup(x);
}
void splay(int x,int k){if (!x)return;if (!k)root=x;for (int y=fa[x];fa[x]!=k;rotate(x),y=fa[x])if (fa[y]!=k)rotate(wson(x)==wson(y)?y:x);
}
int find(int x,int v){return val[x]==v?x:find(son[x][v>val[x]],v);
}
int findkth(int x,int k){if (k<=tot[son[x][0]])return findkth(son[x][0],k);k-=tot[son[x][0]];if (k<=cnt[x])return x;k-=cnt[x];return findkth(son[x][1],k);
}
int findnxt(int x,int v){if (!x)return 0;if (val[x]<=v)return findnxt(son[x][1],v);else {int res=findnxt(son[x][0],v);return res?res:x;}
}
int findpre(int x,int v){if (!x)return 0;if (val[x]>=v)return findpre(son[x][0],v);else {int res=findpre(son[x][1],v);return res?res:x;}
}
void insert(int &x,int pre,int v){if (!x){x=++size;val[x]=v,cnt[x]=tot[x]=1,fa[x]=pre;splay(x,0);return;}tot[x]++;if (val[x]==v){cnt[x]++;return;}insert(son[x][v>val[x]],x,v);
}
void Insert(int v){insert(root,0,v);}
void Delete(int v){int x;splay(x=find(root,v),0);if (--cnt[x])return;splay(findnxt(root,v),root);root=son[x][1];son[root][0]=son[x][0];fa[son[x][0]]=root;fa[root]=son[x][0]=son[x][1]=0;pushup(root);
}
int Rank(int v){splay(find(root,v),0);return tot[son[root][0]]+1;
}
int main(){val[1]=2147483647;cnt[1]=tot[1]=1;scanf("%d",&n);while (n--){int opt,x;scanf("%d%d",&opt,&x);if (opt==1) Insert(x);if (opt==2) Delete(x);if (opt==3) printf("%d\n",Rank(x));if (opt==4) printf("%d\n",val[findkth(root,x)]);if (opt==5) printf("%d\n",val[findpre(root,x)]);if (opt==6) printf("%d\n",val[findnxt(root,x)]);}return 0;
}

 

替罪羊树

1.思想

如果数据是随机的，那么直接暴力插入节点就AC了。

但是直接卡成一条链就TLE了。

那么我们来想想办法。

定期重构？

可以得到 $O(n\sqrt n)$ 的优秀复杂度。

 

这个东西不够智能，我们来给他升升级！

替罪羊树：当一棵子树的左右儿子不平衡到一定程度的时候，我们将整个子树暴力重构。

具体地，我们要设定一个参数 c ，当一个节点的其中左子树或者右子树占当前子树的比重超过c的时候，就将这个子树暴力重构。

注意，暴力重构的时候要从上往下，这样只重构最大的需要被重构的子树，常数较小。

c 的取值一般在 $0.5~1$ 之间，不能取 1 （取1的时候就是暴力），也不要取 0.5 （重构次数太多导致TLE），取 0.75~0.85 差不多就好了。

关于时间复杂度：

首先，树高显然是 $O(\log n)$ 的，所以查询的复杂度是对的。

我们来看看重构的复杂度是什么。

定义势函数 $\phi(T) = \sum_{x} {abs(size[ls]-size[rs])}$ （假设 ls 是 x 的左儿子，rs 是 x 的右儿子），那么，由于树高是 $O(\log n)$ 的，所以显然插入一个节点最多使 $\phi(T)$ 增加 $O(\log n)$ 。

每次暴力重构点 x 的时候，消耗了 $O(size[x])$ 的时间复杂度，使 $\phi(T)$ 至少减少了 $O(size[x]) \times (c-(1-c)) = O(size[x]\cdot (2c-1))$ ，所以重构的时间复杂度是均摊 $O(\log n)$ 的。

2.一道模板题

UOJ#55 紫荆花之恋

替罪羊树思想不一定只能放在平衡树上，还可以放在点分树上。

不过这题还要套个平衡树，可以用splay + 卡常数，或者 Treap 。

代码

#pragma GCC optimize("Ofast","inline")
#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
#define For(i,a,b) for (int i=a;i<=b;i++)
#define Fod(i,b,a) for (int i=b;i>=a;i--)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define _SEED_ ('C'+'L'+'Y'+'A'+'K'+'I'+'O'+'I')
#define outval(x) printf(#x" = %d\n",x)
#define outvec(x) printf("vec "#x" = ");for (auto _v : x)printf("%d ",_v);puts("")
#define outtag(x) puts("----------"#x"----------")
using namespace std;
typedef long long LL;
LL read(){LL x=0,f=0;char ch=getchar();while (!isdigit(ch))f|=ch=='-',ch=getchar();while (isdigit(ch))x=(x<<1)+(x<<3)+(ch^48),ch=getchar();return f?-x:x;
}
const int N=100005,INF=1.05e9,mod=1e9;
const double checkval=0.80;
namespace spl{const int S=N*100;int son[S][2],fa[S],val[S],size[S];int cnt=0;namespace cly{int st[S],top=0;inline int new_node(){return top?st[top--]:++cnt;}inline void Recover(int x){st[++top]=x;son[x][0]=son[x][1]=fa[x]=val[x]=size[x]=0;}}using cly::new_node;using cly::Recover;#define ls son[x][0]#define rs son[x][1]int new_node(int v){int x=new_node();val[x]=v;return x;}inline void pushup(int x){size[x]=size[ls]+size[rs]+1;}inline int wson(int x){return son[fa[x]][1]==x;}void rotate(int x){int y=fa[x],z=fa[y],L=son[y][1]==x,R=L^1;if (z)son[z][son[z][1]==y]=x;fa[x]=z,fa[y]=x,fa[son[x][R]]=y;son[y][L]=son[x][R],son[x][R]=y;pushup(y),pushup(x);}void splay(int x){for (int y=fa[x];fa[x];rotate(x),y=fa[x])if (fa[y])rotate(wson(x)==wson(y)?y:x);}inline void Ins(int &a,int v){register int x=a,c=0;int f=0;while (x){c++;size[x]++;f=x;x=v<val[x]?ls:rs;}val[son[f][v>=val[f]]=x=new_node()]=v,fa[x]=f,size[x]=1;if (!a||c>30)splay(a=x);}int Query(int &rt,int v){int ans=0,c=0;register int x=rt,p=0;while (x){p=x,c++;if (val[x]<=v)ans+=size[ls]+1,x=rs;elsex=ls;}if (p&&c>30)splay(rt=p);return ans;}void Remove(int x){if (x)Remove(ls),Remove(rs),Recover(x);}int id[N];void Build(int &x,int L,int R,int f){if (L>R)return;int mid=(L+R)>>1;fa[x=id[mid]]=f;Build(ls,L,mid-1,x);Build(rs,mid+1,R,x);pushup(x);}void Build(int &x,vector <int> &v){if (v.empty())return;int n=0;sort(v.begin(),v.end());for (auto i : v)id[++n]=new_node(i);Build(x,1,n,0);}#undef ls#undef rs
}
int Test,n;
LL ans=0;
vector <int> e[N];
int fa[N][20],depth[N],len[N];
int LCA(int x,int y){if (depth[x]<depth[y])swap(x,y);Fod(i,16,0)if (depth[x]-(1<<i)>=depth[y])x=fa[x][i];if (x==y)return x;Fod(i,16,0)if (fa[x][i]!=fa[y][i])x=fa[x][i],y=fa[y][i];return fa[x][0];
}
int Dis(int x,int y){return len[x]+len[y]-2*len[LCA(x,y)];
}
int r[N];
namespace dt{int fa[N],size[N],mxs[N],depth[N];int rt[N],rtf[N];int node_cnt=0;void Init(){clr(fa),clr(size),clr(mxs),clr(depth),clr(rt),clr(rtf);depth[0]=-1,node_cnt++;size[1]=1,mxs[1]=depth[1]=rt[1]=0;spl::Ins(rt[1],0-r[1]);}int id[N],idc=0;void dfs(int x,int pre,int d){id[++idc]=x;for (auto y : e[x])if (y!=pre&&depth[y]>=d)dfs(y,x,d);}int sz[N],msz[N],RT,Size;void dfs2(int x,int pre){sz[x]=1,msz[x]=0;for (auto y : e[x])if (y!=pre&&!size[y]){dfs2(y,x);sz[x]+=sz[y];msz[x]=max(msz[x],sz[y]);}msz[x]=max(msz[x],Size-sz[x]);if (!RT||msz[x]<msz[RT])RT=x;}vector <int> id1,id2;void dfs3(int x,int pre,int anc){sz[x]=1;id1.pb(Dis(x,anc)-r[x]);if (fa[anc])id2.pb(Dis(x,fa[anc])-r[x]);for (auto y : e[x])if (y!=pre&&!size[y])dfs3(y,x,anc),sz[x]+=sz[y];}void build(int x,int f,int n){RT=0,Size=n;dfs2(x,0);x=RT;fa[x]=f,depth[x]=depth[f]+1,size[x]=n,mxs[x]=msz[x];id1.clear(),id2.clear();dfs3(x,0,x);spl::Build(rt[x],id1);spl::Build(rtf[x],id2);for (auto y : e[x])if (!size[y])build(y,x,sz[y]);}void Rebuild(int x,int f){idc=0;dfs(x,0,depth[x]);For(_t,1,idc){int i=id[_t];spl::Remove(rt[i]),spl::Remove(rtf[i]);depth[i]=size[i]=fa[i]=mxs[i]=rt[i]=rtf[i]=0;}build(x,f,idc);}void Ins(int x,int f){static vector <int> v;fa[x]=f,depth[x]=depth[f]+1;rt[x]=rtf[x]=0;v.clear();for (int i=x;i;i=fa[i]){v.pb(i),size[i]++;mxs[fa[i]]=max(mxs[fa[i]],size[i]);spl::Ins(rt[i],Dis(i,x)-r[x]);if (fa[i])spl::Ins(rtf[i],Dis(fa[i],x)-r[x]);}node_cnt++;reverse(v.begin(),v.end());for (auto i : v)if (mxs[i]>checkval*size[i]){Rebuild(i,fa[i]);break;}if (size[x]>1)ans+=spl::Query(rt[x],r[x])-1;for (int i=x,f,d;depth[i];i=f){f=fa[i],d=Dis(f,x);ans+=spl::Query(rt[f],r[x]-d)-spl::Query(rtf[i],r[x]-d);}}
}
int main(){Test=read(),n=read();For(i,1,n){int f=read()^(ans%mod),c=read();r[i]=read();if (!f){dt::Init();printf("%lld\n",ans);continue;}assert(1<=f&&f<i);e[i].pb(f),e[f].pb(i);fa[i][0]=f;For(j,1,16)fa[i][j]=fa[fa[i][j-1]][j-1];depth[i]=depth[f]+1;len[i]=len[f]+c;dt::Ins(i,f);printf("%lld\n",ans);}return 0;
}

 

非旋Treap

1. Treap 简介

Treap = Tree + Heap 。

我们考虑给每一个节点随机赋一个值 ckv ，假设这个节点本来的值是 val，那么，我们建一个平衡树，满足对于 val，它是个二叉搜索树，对于 ckv 它满足堆性质，就是满足 $val[ls]\leq val[x]\leq val[rs], ckv[x]\leq ckv[ls], ckv[x] \leq ckv[rs]$。

可以证明这样的树是唯一的。

由于它的随机的，所以树高是 $O(\log n)$ 的。

我们来看看插入节点的时候怎么维护它的性质：旋转！首先插入到一个满足二叉搜索树性质的位置，然后，如果 ckv[x] < ckv[fa[x]] ，那么将 x 上旋，直到满足这个条件为止。

这个需要旋转的 Treap 有一定的局限性，接下来介绍功能更加强大的非旋 Treap 。

2. Merge

合并 Treap x 和 Treap y，需要保证 x 中的任意元素小于 y 中的任意元素。

假设 x 为空，则返回 y 。

假设 y 为空，则返回 x 。

假设 ckv[x] < ckv[y] ，则将点 x 作为根， rs[x] = Merge(rs[x], y)

否则，将点 y 作为根， ls[y] = Merge(x, ls[y])  （注意这里 x 要放在前面）

时间复杂度 $O(\log n)$ 。

代码：

    int Merge(int x,int y){if (!x||!y)return x+y;if (ckv[x]<ckv[y]){son[x][1]=Merge(son[x][1],y),pushup(x);return x;}else {son[y][0]=Merge(x,son[y][0]),pushup(y);return y;}}

3. Split

这个函数的作用就是将一个平衡树前 k 小节点构成的平衡树和剩余节点构成的平衡树。时间复杂度 $O(\log n)$ 。

直接看代码很容易理解的。

代码：

    pair <int,int> Split(int x,int k){if (!x)return mp(0,0);if (k<=size[ls]){pair <int,int> p=Split(ls,k);ls=p.se,pushup(x);return mp(p.fi,x);}else {pair <int,int> p=Split(rs,k-size[ls]-1);rs=p.fi,pushup(x);return mp(x,p.se);}}

4. 其他操作

Rank ： 直接写。

Find-Kth = Split + Merge 

Insert = Rank + Split + Merge + Merge

Delete = Split + Split + Merge

区间修改：由于每次操作都是自顶向下的，所以可以进行标记下传，所以支持区间修改。

可持久化：由于每次操作都是自顶向下的，而且只改变节点的儿子，所以是可以可持久化的。这一点其他平衡树都做不了。

5. 模板(BZOJ3224)

#include <bits/stdc++.h>
#define clr(x) memset(x,0,sizeof (x))
#define For(i,a,b) for (int i=a;i<=b;i++)
#define Fod(i,b,a) for (int i=b;i>=a;i--)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define _SEED_ ('C'+'L'+'Y'+'A'+'K'+'I'+'O'+'I')
#define outval(x) printf(#x" = %d\n",x)
#define outvec(x) printf("vec "#x" = ");for (auto _v : x)printf("%d ",_v);puts("")
#define outtag(x) puts("----------"#x"----------")
using namespace std;
typedef long long LL;
LL read(){LL x=0,f=0;char ch=getchar();while (!isdigit(ch))f|=ch=='-',ch=getchar();while (isdigit(ch))x=(x<<1)+(x<<3)+(ch^48),ch=getchar();return f?-x:x;
}
const int N=100005;
int randint(){
#ifdef windowsreturn (rand()<<15)^rand();
#elsereturn rand();
#endif
}
namespace Treap{const int S=N;int son[N][2],size[N],val[N],ckv[N];int cnt=0;#define ls son[x][0]#define rs son[x][1]int new_node(int v){cnt++,val[cnt]=v,ckv[cnt]=randint(),size[cnt]=1;return cnt;}void pushup(int x){size[x]=size[ls]+size[rs]+1;}int Merge(int x,int y){if (!x||!y)return x+y;if (ckv[x]<ckv[y]){son[x][1]=Merge(son[x][1],y),pushup(x);return x;}else {son[y][0]=Merge(x,son[y][0]),pushup(y);return y;}}pair <int,int> Split(int x,int k){if (!x)return mp(0,0);if (k<=size[ls]){pair <int,int> p=Split(ls,k);ls=p.se,pushup(x);return mp(p.fi,x);}else {pair <int,int> p=Split(rs,k-size[ls]-1);rs=p.fi,pushup(x);return mp(x,p.se);}}int Find(int x,int v){return x?(val[x]==v?x:Find(son[x][val[x]<v],v)):0;}int _Rank(int x,int v){return x?(val[x]>v?_Rank(ls,v):size[ls]+1+_Rank(rs,v)):0;}int Rank(int x,int v){return _Rank(x,v-1);}void Insert(int &x,int v){pair <int,int> p=Split(x,_Rank(x,v));x=Merge(p.fi,Merge(new_node(v),p.se));}void Delete(int &x,int v){int rk=Rank(x,v);pair <int,int> pL=Split(x,rk),pR=Split(pL.se,1);x=Merge(pL.fi,pR.se);}int QRank(int x,int v){return Rank(x,v)+1;}int Find_Kth(int x,int k){return k==size[ls]+1?x:(k<=size[ls]?Find_Kth(ls,k):Find_Kth(rs,k-size[ls]-1));}int Get_pre(int &x,int v){return Find_Kth(x,Rank(x,v));}int Get_nxt(int &x,int v){return Find_Kth(x,_Rank(x,v)+1);}#undef ls#undef rs
}
using namespace Treap;
int n,root=0;
int main(){srand(_SEED_);n=read();while (n--){int opt=read(),x=read();if (opt==1)Insert(root,x);else if (opt==2)Delete(root,x);else if (opt==3)printf("%d\n",QRank(root,x));else if (opt==4)printf("%d\n",val[Find_Kth(root,x)]);else if (opt==5)printf("%d\n",val[Get_pre(root,x)]);else if (opt==6)printf("%d\n",val[Get_nxt(root,x)]);}return 0;
}

一些题目(点击进入)