做爰网站名称/百度广告一级代理

小波变换去噪

桥梁实时监测系统所处环境复杂，信号传输距离较远，不可避免的受到外界的干扰，这些干扰统称为白噪声，它可以使实时监测系统无法甚至错误的工作。信号被噪声污染的程度可用信噪比 SNR（Signal-to-Noise Ratio）来表示：

（单位：dB） （3-2）

式中：

——信号的方差。

——噪声的方差。

当SNR较小时，实际信号被淹没在噪声中，造成信号识别困难。因此信号处理的第一步是信号和噪声的分离，然后才可以进行后续分析工作。消除信号噪声的方法很多，如维纳滤波、卡尔曼滤波、自适应滤波等，在信号频域进行去噪是以Fourier变换为主的。传统的去噪方法是将被噪音污染的信号通过一个滤波器，滤除掉噪音频率成分。但对于瞬间信号、宽带噪音信号、非平稳信号等，采用传统方法具有一定的局限性。本文应用小波多尺度分析的方法进行去噪。一般情况下，去噪过程可以按照图 3.5所示流程来进行。

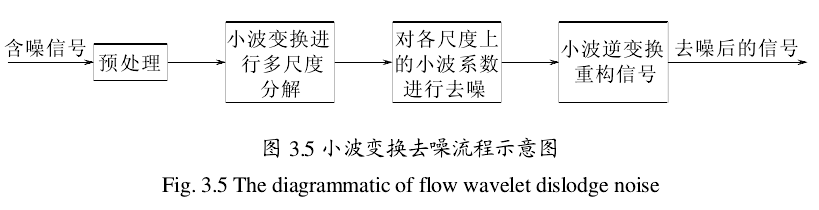
1 去噪原理

一个含噪声的一维信号的模型可以表示成如下形式，即

     

(3-3)

其中：f(t)——真实信号。

 e(t)——噪声。

 s(t)——含噪声的信号。

在实际的工程应用中，有用信号通常表现为低频信号或是一些比较平稳的信号，而噪声信号通常表现为高频信号。这就为小波分析消噪提供了前提条件。如果以一个最简单的噪声模型加以说明，即认为e(t)为一实的、均值为零的宽平稳的高斯白噪声。

是e(t)小波变换。设小波

是实的，从而有：

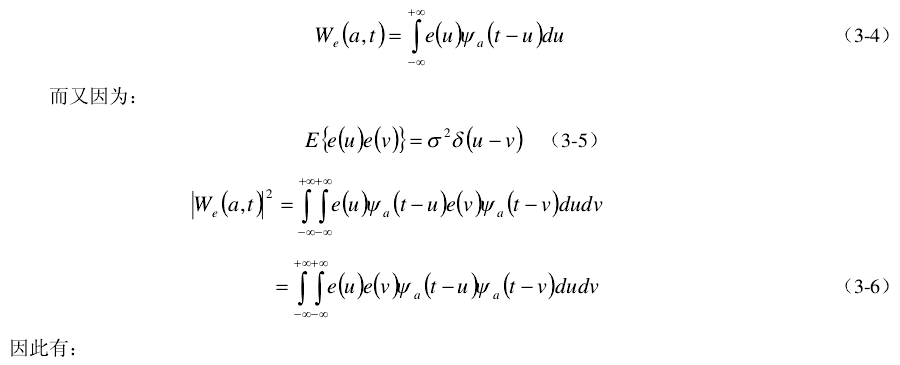
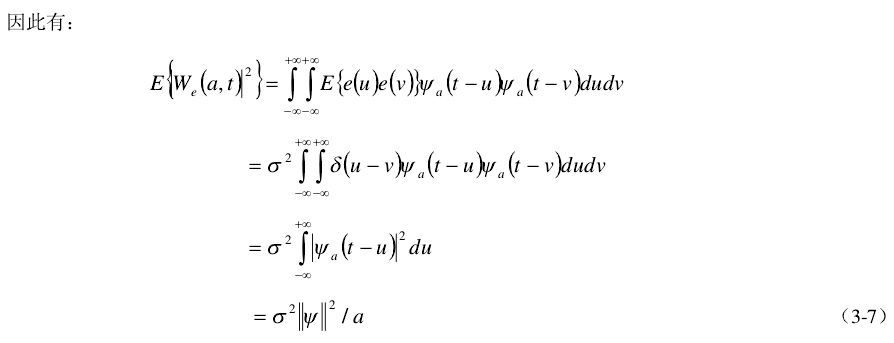
这表明噪音小波变换后

的平均功率与尺度a成反比，这是小波去噪的理论基础。对信号f(t)的就是要抑制信号中的噪声部分e(t),而恢复出真实信号s(t)。因此，可以利用噪音与信号小波分析后各尺度上表现的不同特性来抑制噪音。

实际信号中常混有随机噪声，随机噪声往往导致信号的奇异性。信号奇异性可以用 Lipschitz指数来描述，这个指数定义如下：设信号

，若f(t)在t0处奇异性为η，是指对t0的某邻域的任意t有：

（3-8）

式中，k为常数。则称f(t)在t0处的Lipschitz指数为η。函数在某一点的Lipschitz指数的大小反映了该点奇异性的大小，η越大，该点的光滑度越高；η越小，该点的奇异性越大。

信号f(t)在[a,b]上有一致Lipschitz指数η的充要条件是存在一个常数k>0，得任意

，f(t)的二进制小波变换满足：

（3-9）

可以看出，如果f(t)的Lipschitz 指数η>0，则该信号的小波变换模极大值幅度将随着尺度的增大而增大；反之，若η<0则f(t)的小波变换系数将随着尺度的增大而减小。一般来说，信号f(t)的Lipschitz指数η>0，因为信号一般都是连续的非奇异信号，即使是不连续的奇异信号，它也一不定会在某一邻域内有界，也有η=0。而噪声一般是均值为零、方差为σ2一个广义随机过程，该过程几乎处处奇异，所以它的Lipschitz指数η<0，其中高斯白噪声的Lipschitz指数

，也就是信号和噪声在不同尺度下的小波变换特性截然相反，随着尺度的增大，信号的小波变换模极大值增大，而噪声的模极大值减小。因此我们可以利用此特性，采用由粗到精的方法跟踪各尺度下的小波变换模极大值，将属于噪声的去掉，再进行重构信号，从而得到逼近真实的信号。

2 去噪的实现

噪声的种类多种多样，但从宏观角度可分为两类：确定性噪声和不确定性噪声。在去噪过程中，对于确定性噪声，由于我们知道其频率或频率范围，只需利用小波变换的特性将该频段信号去掉即可；对于不确定性噪声，我们不知道其频率范围，一般认为是白噪声，白噪声的频率分布较广，此时，只能利用小波分析的多分辨率特性进行去噪了。

对f(t)连续几次小波变换之后，信号s(t)所对应的各尺度上的小波系数在某些特定的位置有较大的值，而在其他大部分位置的小波系数则较小。对于白噪声e(t)，它对所有小波系数的影响基本上一样的，并随着尺度的增大而幅值有所减少。因此，我们可以选用一定的阀值λ，把抵于λ的小波系数归零，把高于λ的小波系数重构原始信号，具体实现方法如下：

①信号f(t)的小波分解。选择一个小波并确定分解的层数，然后进行分解计算。

②小波分解高频系数的阀值量化。对各个分解尺度下的高频系数选择一个阀值进行软阀值量化处理。

③一维小波重构。根据小波分解的底层低频系数和各层高频系数进行一维小波重构。应用小波分析进行信号降噪处理，主要通过Matlab的两个函数wden和wdencmp来实现。Wden函数返回的是经过对原始信号进行降噪处理后的信号。Wdencmp函数是一种使用更为普遍的函数，它可以直接对一维或二维信号进行降噪，处理方法也是通过对小波分解系数进行阀值量化来实现。

Matlab 中小波分析进行阀值处理一般有下述 3 种方法。

①默认阀值消噪处理。该方法利用函数ddencmp生成信号的默认阀值，然后利用函数 wdencmp进行消噪处理。

②给定阀值消噪处理。在实际的消噪处理过程中，阀值往往可通过经验公式获得，且这种阀值的可信度高。在进行阀值量化处理时可用函数wthresh。

③强制消噪处理。该方法是将小波分解结构中的高频系数全部置为0，即滤掉所有高频部分，然后对信号进行小波重构。这种方法简便，消噪后的信号比较平滑，但容易丢失信号中的有用成分。

《来源科技文献，经本人分析整理，以技术会友，广交天下朋友》