苏州网站建设设计公司哪家好/优化设计单元测试卷

1. 这个特征有什么意义？

         先来看离散、连续卷积的定义式特征：

从举一个离散卷积的例子——掷骰子……有两枚骰子：

求：两枚骰子点数加起来为4的概率是多少?

这里问题的关键是，两个骰子加起来要等于4，这正是卷积的应用场景。

我们把骰子各个点数出现的概率表示出来：

那么，两枚骰子点数加起来为4的情况有以下几种：

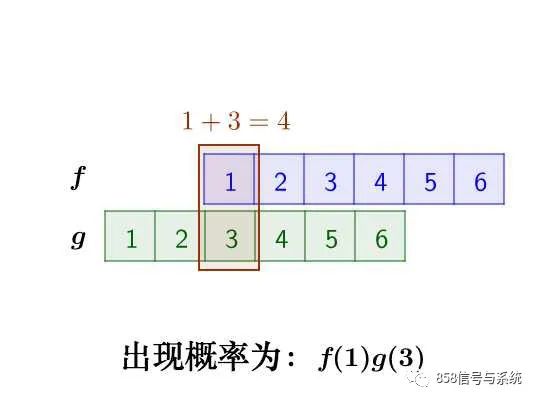
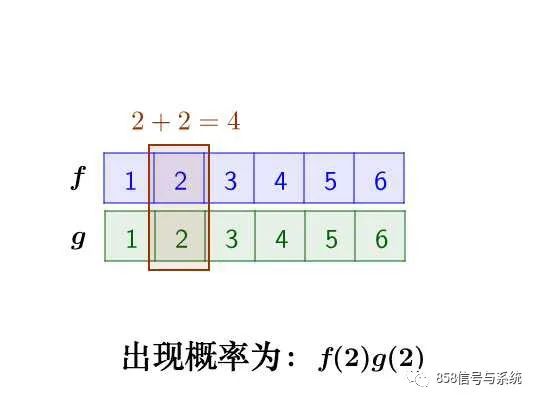
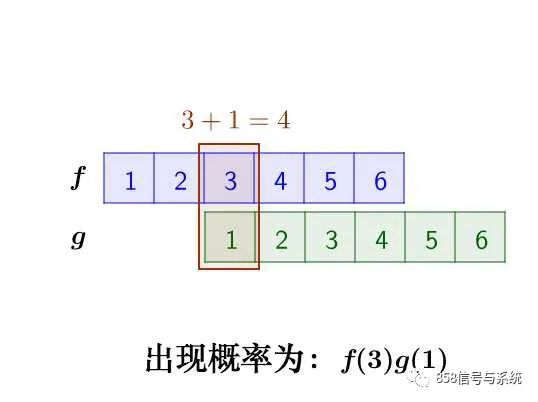
因此，两枚骰子点数加起来为4的概率为：

举个连续卷积的例子：做馒头

本科期间的信号与系统里面经常讲到卷积(convolution)，自动控制原理里面也会经常有提到卷积。硕士期间的线性系统理论与数字信号处理，里面也是各种大把大把卷积的概念。卷积神经网络(Convolutional Neural Network, CNN)，在图像领域取得了非常好的实际效果，已经把传统的图像处理的方法快干趴下了。然而对卷积的物理意义的理解并不是那么清晰。

首先，这样通俗简单地去理解卷积--

已知x[0] = a, x[1] = b, x[2]=c

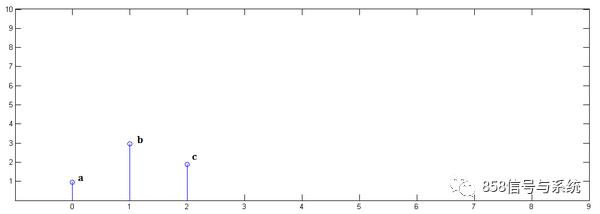
y[0] = i, y[1] = j, y[2]=k

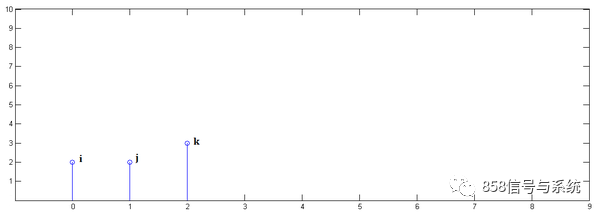
下面通过演示求x[n] * y[n]的过程，揭示卷积的物理意义。

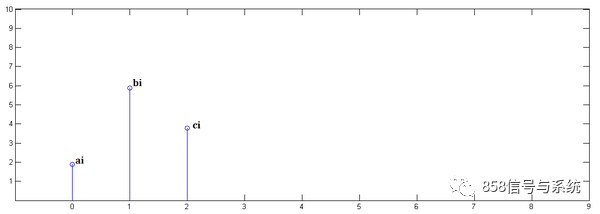
第一步，x[n]乘以y[0]并平移到位置0：

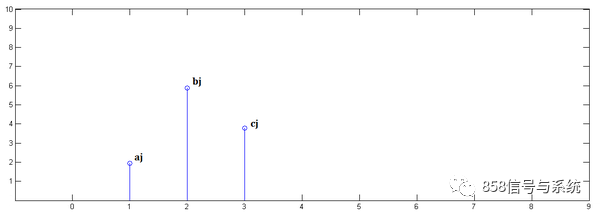
第二步，x[n]乘以y[1]并平移到位置1

第三步，x[n]乘以y[2]并平移到位置2

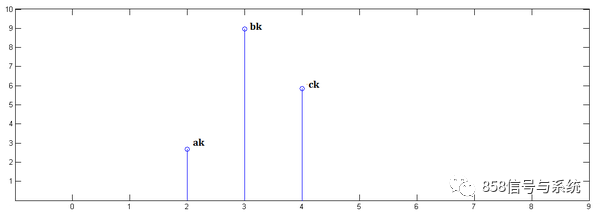
最后，把上面三个图叠加，就得到了x[n] * y[n]：

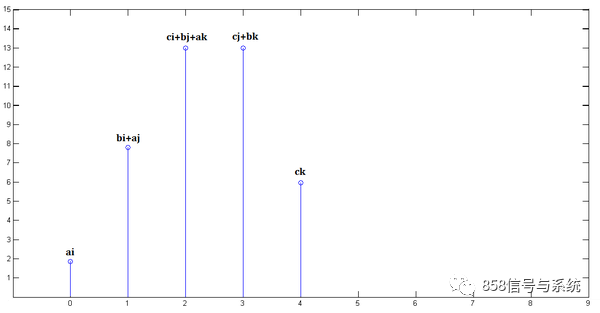
从这里，可以看到卷积的重要的物理意义是：一个函数(如：单位响应)在另一个函数(如：输入信号)上的加权叠加。

重复一遍，这就是卷积的意义：加权叠加。

对于线性时不变系统，如果知道该系统的单位响应，那么将单位响应和输入信号求卷积，就相当于把输入信号的各个时间点的单位响应 加权叠加，就直接得到了输出信号。

通俗的说：

在输入信号的每个位置，叠加一个单位响应，就得到了输出信号。

这正是单位响应是如此重要的原因。

可以看出这两种做法区别在于：①先反褶再平移，把输入信号当作一个整体，一次算出一个时间点的响应值；②把信号拆开，一次算出一个信号在所有时间的响应值，再把各个信号相加。两者本质上是相同的。

2.卷积的另外解释

卷积表示为y(n)=x(n)∗h(n)

使用离散数列来理解卷积会更形象一点，我们把y(n)的序列表示成y(0),y(1),y(2),⋯, 这是系统响应出来的信号。

同理，x(n)的对应时刻的序列为x(0),x(1),x(2),⋯

其实我们如果没有学过信号与系统，就常识来讲，系统的响应不仅与当前时刻系统的输入有关，也跟之前若干时刻的输入有关，因为我们可以理解为这是之前时刻的输入信号经过一种过程(这种过程可以是递减，削弱，或其他)对现在时刻系统输出的影响，那么显然，我们计算系统输出时就必须考虑现在时刻的信号输入的响应以及之前若干时刻信号输入的响应之“残留”影响的一个叠加效果。

假设0时刻系统响应为y(0),若其在1时刻时，此种响应未改变，则1时刻的响应就变成了y(0)+y(1),叫序列的累加和(与序列的和不一样)。但常常系统中不是这样的，因为0时刻的响应不太可能在1时刻仍旧未变化，那么怎么表述这种变化呢，就通过h(t)这个响应函数与x(0)相乘来表述，表述为x(m)×h(m−n)，具体表达式不用多管，只要记着有大概这种关系，引入这个函数就能够表述y(0)在1时刻究竟削弱了多少，然后削弱后的值才是y(0)在1时刻的真实值，再通过累加和运算，才得到真实的系统响应。

再拓展点，某时刻的系统响应往往不一定是由当前时刻和前一时刻这两个响应决定的，也可能是再加上前前时刻，前前前时刻，前前前前时刻，等等，那么怎么约束这个范围呢，就是通过h(n)这个函数在表达式中变化后的h(m−n)中的m的范围来约束的。即说白了，就是当前时刻的系统响应与多少个之前时刻的响应的“残留影响”有关。

3.卷积的数学定义

4.卷积的应用

用一个模板和一幅图像进行卷积，对于图像上的一个点，让模板的原点和该点重合，然后模板上的点和图像上对应的点相乘，然后各点的积相加，就得到了该点的卷积值。对图像上的每个点都这样处理。由于大多数模板都是对称的，所以模板不旋转。卷积是一种积分运算，用来求两个曲线重叠区域面积。可以看作加权求和，可以用来消除噪声、特征增强。

把一个点的像素值用它周围的点的像素值的加权平均代替。

卷积是一种线性运算,图像处理中常见的mask运算都是卷积，广泛应用于图像滤波。

卷积关系最重要的一种情况，就是在信号与线性系统或数字信号处理中的卷积定理。利用该定理，可以将时间域或空间域中的卷积运算等价为频率域的相乘运算，从而利用FFT等快速算法，实现有效的计算，节省运算代价。

从数学上讲，卷积就是一种运算。

某种运算，能被定义出来，至少有以下特征：

1.首先是抽象的、符号化的

2.其次，在生活、科研中，有着广泛的作用

最后看看图像处理上的卷积～～

有这么一副图像，可以看到，图像上有很多噪点：

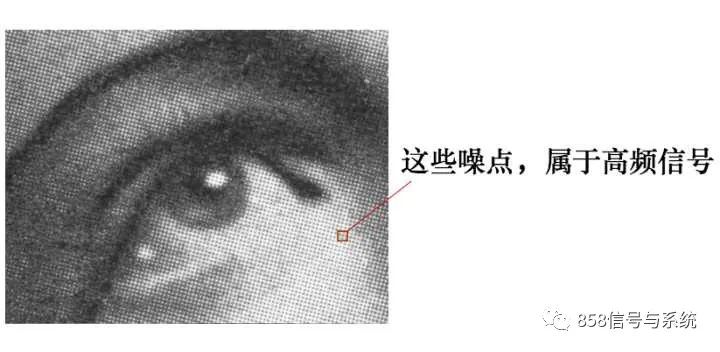
高频信号，就好像平地耸立的山峰，看起来很显眼。

平滑这座山峰的办法之一就是，把山峰刨掉一些土，填到山峰周围去。用数学的话来说，就是把山峰周围的高度平均一下。

平滑后得到

卷积可以帮助实现这个平滑算法。

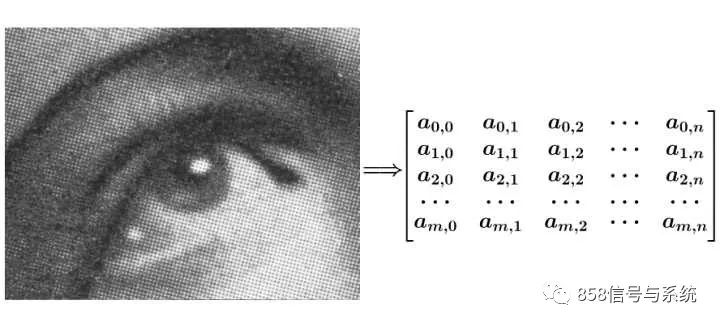
有噪点的原图，可以把它转为一下矩阵~

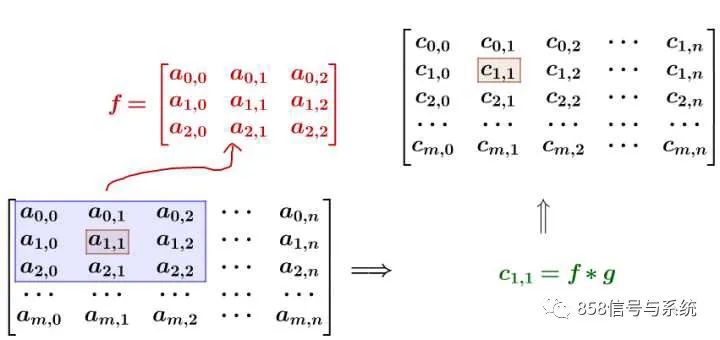
要注意一点，为了运用卷积， g 虽然和 f 同维度，但下标有点不一样：