目录

一.结点的定义

二.递归法遍历二叉树

前序遍历

中序遍历

后序遍历

三.迭代（非递归）遍历二叉树

（1）.迭代模拟法

前序遍历

中序遍历

后序遍历

（2）.空指针标记法

前序遍历

中序遍历

后序遍历

（3）.一些散的简便方法

前序遍历

后序遍历

一.结点的定义

首先这里先给出结点的定义，和leetcode树相关的题目都是这么定义结点的

class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}}

二.递归法遍历二叉树

前序遍历

遍历二叉树，将二叉树的前序序列存放到list中，对标LeetCode144题，94题，145题

class Solution {List<Integer> list = new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {if(root != null){list.add(root.val);  //这里表示的是对结点的操作preorderTraversal(root.left);preorderTraversal(root.right);}return list;}
}

中序遍历

class Solution {List<Integer> list = new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {if(root != null){preorderTraversal(root.left);list.add(root.val);  //这里表示的是对结点的操作preorderTraversal(root.right);}return list;}
}

后序遍历

class Solution {List<Integer> list = new ArrayList<>();public List<Integer> preorderTraversal(TreeNode root) {if(root != null){preorderTraversal(root.left);preorderTraversal(root.right);list.add(root.val);  //这里表示的是对结点的操作}return list;}
}

三.迭代（非递归）遍历二叉树

（1）.迭代模拟法

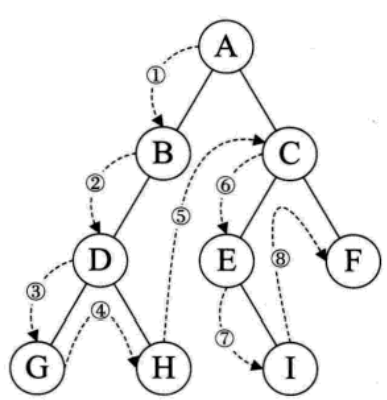
前序和中序的迭代模拟法比较简单，就相当于是把整个二叉树按顺序走了一遍，类似下面的图，前序遍历是第一次访问到结点的时候就输出，中序遍历是第二次访问到结点的时候输出。

这里注意用的是栈，node定义在外面，且根节点不需要先push进入栈，然后就是循环退出条件还要加一个node ！= null，和层序遍历还是不一样的。

前序遍历

class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if (root == null){return null;}Deque<TreeNode> stack = new LinkedList<>();TreeNode node = root;while(!stack.isEmpty() || node != null) {while (node != null) {stack.push(node);list.add(node.val);node = node.left;}node = stack.pop();node = node.right;  //这一步的时候会出现stack里面是空，但是node不是空的情况}return list;}
}

中序遍历

class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> list = new ArrayList<>();if (root == null){return list;}Deque<TreeNode> stack = new LinkedList<>();TreeNode node = root;while(!stack.isEmpty() || node != null){while (node != null){stack.push(node);node = node.left;}node = stack.pop();list.add(node.val);node = node.right;}return list;}
}

后序遍历

后序遍历的话，比前序和中序复杂一点。当一个结点pop出来以后，要判断当时是从哪边遍历上来的。

如果右子树为空，或者右子树之前已经遍历过了，那就是从右边上来的，保存当前node为prev表示已经遍历完了，然后把当前node置空，终止当前node的遍历。

如果右子树不为空而且没有被遍历过，那就是从左边上来的，往右走就行。这里必须再将当前结点push进去，因为当前结点后面还要访问一次。

class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();if (root == null) {return res;}Deque<TreeNode> stack = new LinkedList<>();TreeNode node = root;TreeNode prev = null;while (node != null || !stack.isEmpty()) {while (node != null) {stack.push(node);node = node.left;}node = stack.pop();if (node.right == null || node.right == prev) {//如果右子树为空，或者右子树之前已经遍历过了，那就是从右边上来的，保存当前node为prev表示已经遍历完了//然后把当前node置空，终止当前node的遍历res.add(node.val);prev = node;node = null;} else {  //如果右子树不为空而且没有被遍历过，那就是从左边上来的，往右走就行stack.push(node);  //这里必须再将当前结点push进去，因为当前结点后面还要访问一次node = node.right;}}return res;}
}

（2）.空指针标记法

这种空指针标记法比较通用，思路也比较简单。简单来说就是利用空指针进行标记，以便于可以访问一个结点多次，第二次访问结点的时候再进行一些操作。

注意点：

1. 这里用的是栈，不是队列。所以入栈的时候要先入右子树，再入左子树。相当于是模拟了栈的执行。
2. 取结点的时候用的是peek，要先判断这个结点是不是null结点，不能直接pop出去。如果是null结点，那就表示需要将当前结点pop出来了，先pop出空结点，再取元素，最后再pop。
3. 还是要注意这里是栈，先进后出，如果是前序的话，是先入右子树，再入左子树，最后入根结点，这样出栈的时候就是根左右，也就是对应的前序序列。

前序遍历

class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> st = new Stack<>();if (root != null) st.push(root);while (!st.empty()) {TreeNode node = st.peek();if (node != null) {st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）st.push(node);                          // 添加中节点st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。} else { // 只有遇到空节点的时候，才将下一个节点放进结果集st.pop();           // 将空节点弹出node = st.peek();    // 重新取出栈中元素st.pop();result.add(node.val); // 加入到结果集}}return result;}
}

中序遍历

class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> st = new Stack<>();if (root != null) st.push(root);while (!st.empty()) {TreeNode node = st.peek();if (node != null) {st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）st.push(node);                          // 添加中节点st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）} else { // 只有遇到空节点的时候，才将下一个节点放进结果集st.pop();           // 将空节点弹出node = st.peek();    // 重新取出栈中元素st.pop();result.add(node.val); // 加入到结果集}}return result;}
}

后序遍历

class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> st = new Stack<>();if (root != null) st.push(root);while (!st.empty()) {TreeNode node = st.peek();if (node != null) {st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中st.push(node);                          // 添加中节点st.push(null); // 中节点访问过，但是还没有处理，加入空节点做为标记。if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）         } else { // 只有遇到空节点的时候，才将下一个节点放进结果集st.pop();           // 将空节点弹出node = st.peek();    // 重新取出栈中元素st.pop();result.add(node.val); // 加入到结果集}}return result;}
}

（3）.一些散的简便方法

前序遍历

前序遍历的标记法可以不需要这么麻烦

class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result = new LinkedList<>();Stack<TreeNode> st = new Stack<>();if (root != null) st.push(root);while (!st.empty()) {TreeNode node = st.pop();result.add(node.val);if (node.right!=null) st.push(node.right);  // 添加右节点（空节点不入栈）if (node.left!=null) st.push(node.left);    // 添加左节点（空节点不入栈）}return result;}
}

后序遍历

也可以使用set来进行标记，第一次访问到结点把结点的右左子树入栈，第二次访问再对该结点进行操作。

class Solution {public List<Integer> postorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();if (root == null) {return res;}Deque<TreeNode> stack = new LinkedList<>();Set<TreeNode> set = new HashSet<>();stack.push(root);while (!stack.isEmpty()){TreeNode node = stack.peek();if(!set.contains(node)){set.add(node);if (node.right != null){stack.push(node.right);}if (node.left != null){stack.push(node.left);}}else {res.add(node.val);stack.pop();}}return res;}
}