互联网传媒 网站/chrome浏览器官网入口

原始文章：KDD 2021 | 一种使用真负样本的在线延迟反馈建模

原始论文：https://arxiv.org/pdf/2104.14121.pdf

================================ 先对文章+论文分别做个总结，以便有个大体印象，方便学习

文章

1：先讲了天级怎么建模

2：分析了“样本池里的样本先全部作为负样本，发送给模型训练。等正样本回流的时候，再以补偿正样本的方式以样本流形式发送给模型”这种方法，也就是论文中的“Fake Negative Weighted”FNW，提出了两个不足

(1) FNW中有个强假设，边缘分布q(x)=p(x)，也可以当成观测分布=真实分布，所以论文先通过改进样本流，使得这个假设成立

(2) 先全部作为负样本，发送给模型训练 这种思路可以得到改进，因为大多数样本在10分钟内可以得到回流，所以没必要这样做（这样做的缺点是：在修正之前，假负样本会对模型造成影响）

论文

1：论文先仔细分析了FNW 的很多细节，可以作为文章的详细介绍补充吧；后面提出的改进也是

================================ 下面是文章+论文中没有讲清的细节/重点

2.1 Delayed Feedback Models

除了预测 CVR，DFM 还引入了第二个模型，该模型捕获了预期的点击和转化之间的延迟，并假设延迟分布遵循指数分布。 这两个模型是联合训练的。 请注意，延迟反馈建模也是与研究生存时间分布的生存时间分析[5]密切相关。 在实践中，指数假设可能并不存在。 为了解决这个问题，Yoshikawa 和 Imai [26] 提出用于 CVR 预测的非参数延迟反馈模型表示时间延迟的分布，不假设参数分布。

Ktena等人[12] 还采用了先把每个样本都当做负样本训练，如果回流到正样本，该样本将被复制为正标记并第二次摄取到训练算法中。因此，有偏差的观测数据分布由来自实际数据分布的“所有正样本”+“所有负样本”。为了从偏差分布中学习模型，利用“重要性抽样”提出了两种损失函数FNW和FNC。Yasui[25]提出了一种反馈转移重要性加权算法，其中模型在一定的时间间隔内等待转换。但是，它不允许数据校正，比如对发生在未来重复的正样本做一些校正。为了在模型训练延迟和假负样本之间找到延迟，ESDFM [24] 建模观察到的转化分布与真实的转化分布（阿里的文章）

3 PRELIMINARY

3.2 Fake Negative Weighted

由于观察到的分布与实际分布存在差异分布，采用重要性抽样来校正分布偏移。 Ktena等人 [12] 提出假负加权（FNW）方法。

全文中下面的分布解释是比较难的，博主在这里讲下自己的理解。首先这里有3种分布，真实分布p(y|x)，观测分布q(y|x)，边缘分布p(x) q(x)，关于边缘分布可以看这篇文章

边缘分布_qrlhl的博客-CSDN博客_边缘分布

边缘分布p(x)简单理解就是x的分布，和y无关（论文中x代表特征组成的样本，y代表label，f(theta)x代表模型）。期望一般可以写成积分的形式

p(x)是上述的“概率分布”，p(y|x)是具体的取值（在x这种概率分布下，y的取值是多少），然后再对x y求积分就得到期望，第二行的q(y|x)   1/q(y|x) 是被强拉进来的变量，第三行假设两个边缘分布p(x) q(x)相等，所以 把p(x)直接换成q(x)，然后对 q(x) q(y|x) 求x y的积分（又换回成了期望），也就是可以换算下最后1行的公式

其中𝑞是有偏的观察分布。 由于摄入重复的正样本，观察到的特征分布𝑞(x) 不等价于实际的特征分布 𝑝(x)。FNW假设 𝑝(x) ≈ 𝑞(x)，这可能会给延迟反馈建模带来一些偏差

在 FNW 中，没有设置等待窗口，样本立即设置为负样本送到模型训练。 一旦有回传，又作为正样本送给模型

因此有3个公式，其中q()是观测分布、p()是真实分布。因为y=0的样本在观测分布下，是包含了真实分布下y=0 + y=1的样本，所以观测分布下 y=0情况下特征分布 q(x|y=0) 就等于真实分布下 p(x | y=0, y=1)，后面的 y=0 y=1是所有样本，所以可以不写，就是 𝑞(x|𝑦 = 0) = 𝑝(x)

而观测分布下，y=1情况下和真实分布y=1是一样多的样本，所以两个样本分布也一致  𝑞(x|𝑦 = 1) = 𝑝(x|𝑦 = 1)

在观测分布下，一共有3批样本，负样本作为负样本，正样本作为负样本，正样本作为正样本，所以观测分布下 y=0 的概率 就得在分母上（本来是 1 / 1）再多加个正样本概率了（使用真实分布的就行）。𝑞(𝑦 = 0) = 1 / 1+𝑝 (𝑦=1)

上面的loss函数可以改写成下面这样

4 实时样本延迟反馈建模（解决了FNW中讲到的 q(x)和p(x)不完全相等这个误差问题）
在本节中，我们详细介绍了使用实时负样本建模的细节。 我们首先介绍Defer 中设计的数据管道，它过了两遍负样本来纠正分布偏移。 基于设计的数据管道，Dafer使用重要性抽样来纠正分布偏移

论文 和 公众号文章中的等待窗口这里不一致，公众号里面说10分钟窗口，论文讲“多分类模型”来预测这个等待窗口

上面推导中<3>到<4>中间的一些可以从论文中看，比较简单

5：天级是怎么建模的

文章最开始的思路，但是后来的做法却没有这么做：通过时延模型预估这条样本（7天内的样本）到模型训练时刻已经发生转化的概率，作为该负样本的不确定性，从而给每条负样本一个合理权重，降低假负样本带来的影响

做法：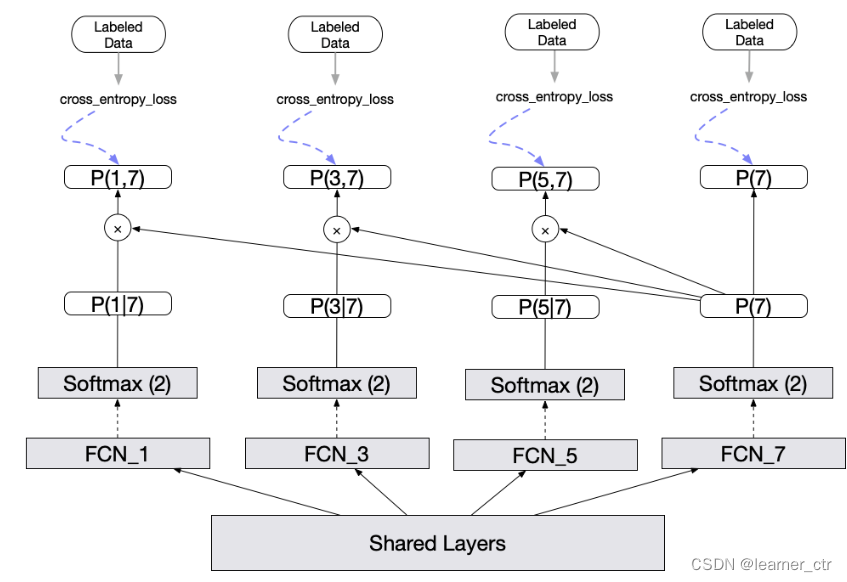

对于7天内的样本，每个都有7个label，分别是1日内转化；2日内转化...；7日内转化

训练模型的时候也是训练这7个label，得到7个label后，根据这条样本距离当前的天数（假设是4天），那么1 2 3这几个label就是已知的（转化或者没转化），就可以求loss(真实label和预测的概率)，可以参与参数更新，4 5 6 7就不能参与更新（如果在1 2 3天内已经转化了，那么4 5 6 7应该也是可以参与更新的。这个在文章中没说到，但是应该是可以的）

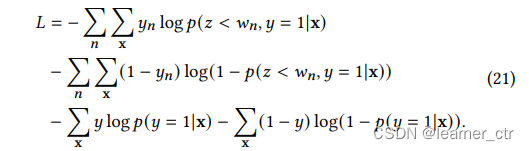
上面是loss的公式，分为两部分，第一部分是p(7)，就是正常7日归因的交叉熵。前面两个有个对n求和，这里的n取值应该是1 2 3 4 5 6（或者像图片中那样只是1 3 5）

线上预估时，只拿p(7)这个预测值即可