类欧几里德算法

概述

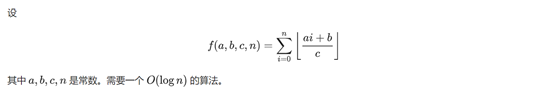
求满足或类似于上式的式子

类型1

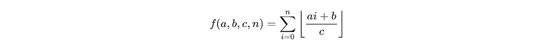
A)当a>c||b>c时

B)当a<c&&b<c时

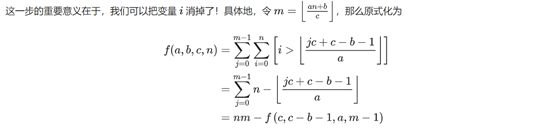
类型2

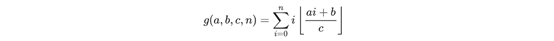
A)当a>c||b>c时

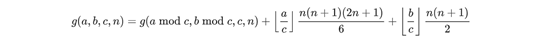
B)当a<c&&b<c时

类型3

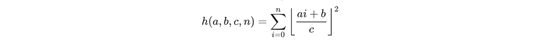
A)当a>c||b>c时

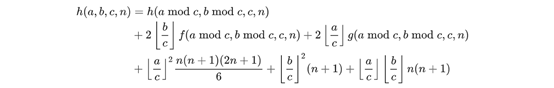
B)当a<c&&b<c时

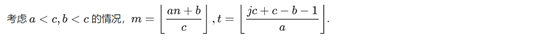
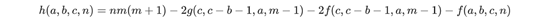
例题

题目描述

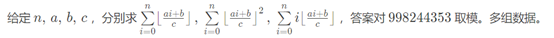
输入格式
第一行给出数据组数 t。
接下来 t行，每行有四个整数，分别为每组数据的 n,a,b,c。

输出格式
对于每组数据，输出一行三个整数，为三个答案对 998244353 取模的结果。

输入样例
2
2 1 0 2
4 3 9 6

输出样例
1 1 2
11 27 27

代码

1.	#include<bits/stdc++.h>  
2.	using namespace std;  
3.	typedef long long ll;  
4.	const ll mod=998244353;  
5.	ll qpow(ll a,ll n)  
6.	{  
7.	    ll ans=1;  
8.	    while(n)  
9.	    {  
10.	        if(n%2) ans=((ans%mod)*(a%mod))%mod;  
11.	        a=((a%mod)*(a%mod))%mod;  
12.	        n/=2;  
13.	    }  
14.	    return ans;  
15.	}  
16.	const ll inv2=qpow(2,mod-2);//2的逆元  
17.	const ll inv6=qpow(6,mod-2);//6的逆元  
18.	struct node  
19.	{  
20.	    ll f,g,h;  
21.	};  
22.	node solve(ll a,ll b,ll c,ll n)  
23.	{  
24.	    node ans,tmp;  
25.	    if(a==0)  
26.	    {  
27.	        ans.f=(n+1)*(b/c)%mod;  
28.	        ans.h=(b/c)*(b/c)%mod*(n+1)%mod;  
29.	        ans.g=((b/c)*n)%mod*(n+1)%mod*inv2%mod;  
30.	        return ans;  
31.	    }  
32.	    if(a>=c||b>=c)  
33.	    {  
34.	        tmp=solve(a%c,b%c,c,n);  
35.	        ans.f=((n*(n+1)%mod*inv2%mod*(a/c)%mod)+(n+1)*(b/c)%mod+tmp.f)%mod;  
36.	        ans.h=((2*(b/c)%mod*tmp.f%mod)+2*(a/c)%mod*tmp.g%mod  
37.	              +(a/c)*(a/c)%mod*n%mod*(n+1)%mod*(2*n+1)%mod*inv6%mod  
38.	              +(b/c)*(b/c)%mod*(n+1)%mod+((a/c)*(b/c)%mod*n%mod*(n+1)%mod)+tmp.h)%mod;  
39.	        ans.g=(tmp.g+(a/c)*n%mod*(n+1)%mod*(2*n+1)%mod*inv6%mod+(b/c)*(n+1)%mod*n%mod*inv2%mod)%mod;  
40.	        return ans;  
41.	    }  
42.	    ll m=(a*n+b)/c;  
43.	    tmp=solve(c,c-b-1,a,m-1);  
44.	    ans.f=(n*(m%mod)%mod-tmp.f)%mod;  
45.	    ans.g=((m*n%mod*((n+1)%mod)%mod-tmp.h-tmp.f)%mod*inv2)%mod;  
46.	    ans.h=((n*(m%mod))%mod*((m+1)%mod)%mod-2*tmp.g-2*tmp.f-ans.f)%mod;  
47.	    return ans;  
48.	}  
49.	int main()  
50.	{  
51.	    ll t;  
52.	    cin>>t;  
53.	    while(t--)  
54.	    {  
55.	        ll a,b,c,n;  
56.	        cin>>n>>a>>b>>c;  
57.	        node ans=solve(a,b,c,n);  
58.	        cout<<(ans.f+mod)%mod<<" "<<(ans.h+mod)%mod<<" "<<(ans.g+mod)%mod<<endl;//由于最后可能为负，处理答案  
59.	    }  
60.	    return 0;  
61.	}