您现在的位置是:主页 > news > 长沙景点排行榜/seo优化诊断工具
长沙景点排行榜/seo优化诊断工具
![]() admin2025/5/7 12:18:46【news】
admin2025/5/7 12:18:46【news】
简介长沙景点排行榜,seo优化诊断工具,网站建设运行工作情况总结,宁波网络营销外包推广1 树结构实际应用 1.1 堆排序 1.1.1 堆排序基本介绍 堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。堆是具有以下性质的完全…
1 树结构实际应用
1.1 堆排序
1.1.1 堆排序基本介绍
- 堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为
O(nlogn),它也是不稳定排序。 - 堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆, 注意 : 没有要求结点的左孩子的值和右孩子的值的大小关系。
- 每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
- 大顶堆举例说明:
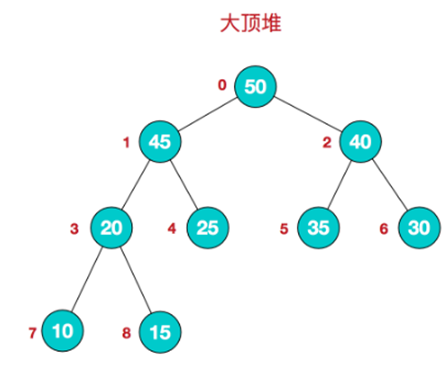
我们对堆中的结点按层进行编号,映射到数组中就是下面这个样子:

5. 小顶堆举例说明
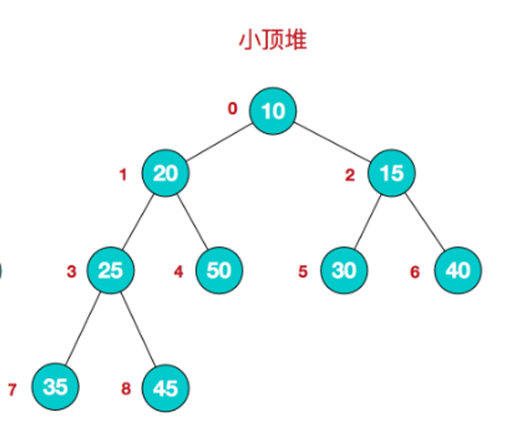
6. 一般升序采用大顶堆,降序采用小顶堆
1.1.2 堆排序的基本思想
- 将待排序序列构造成一个大顶堆
- 此时,整个序列的最大值就是堆顶的根节点。
- 将其与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
可以看到在构建大顶堆的过程中,元素的个数逐渐减少,最后就得到一个有序序列了.
1.1.3 堆排序的思路分析与步骤
步骤一 构造初始堆。将给定无序序列构造成一个大顶堆(一般升序采用大顶堆,降序采用小顶堆)。
-
.假设给定无序序列结构如下

-
.此时我们从最后一个非叶子结点开始(叶结点自然不用调整,第一个非叶子结点 arr.length/2-1=5/2-1=1,也就是下面的6结点),从左至右,从下至上进行调整。
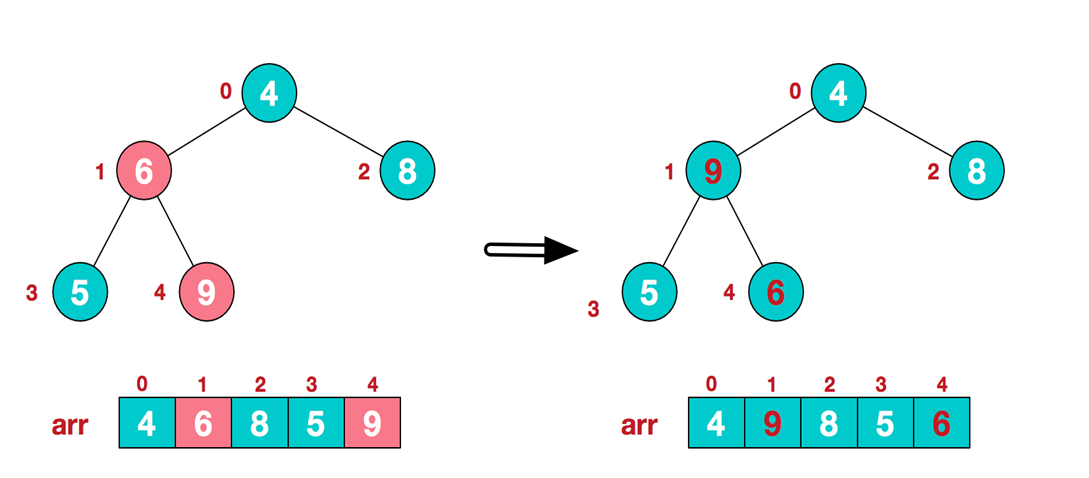
-
.找到第二个非叶节点4,由于[4,9,8]中9元素最大,4和9交换。
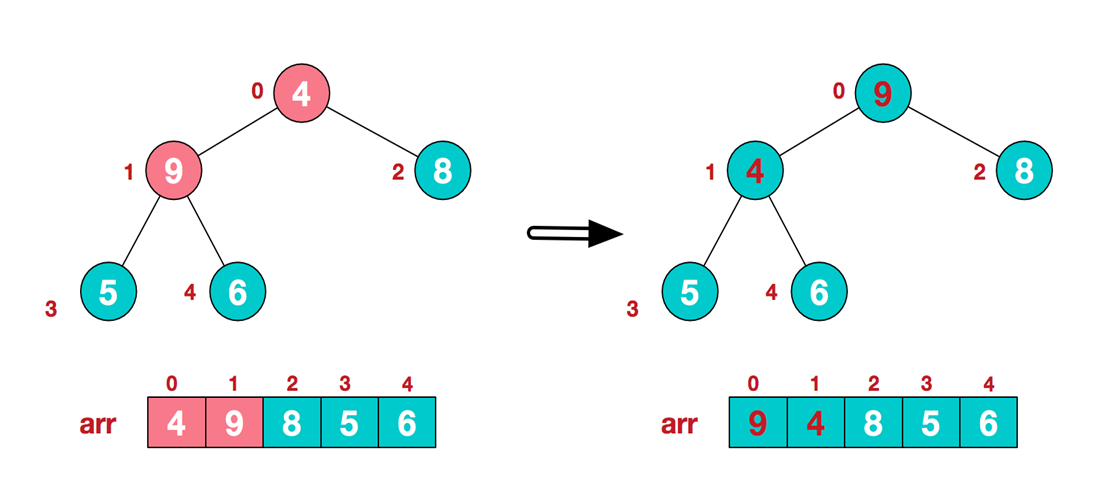
-
这时,交换导致了子根[4,5,6]结构混乱,继续调整,[4,5,6]中6最大,交换4和6。
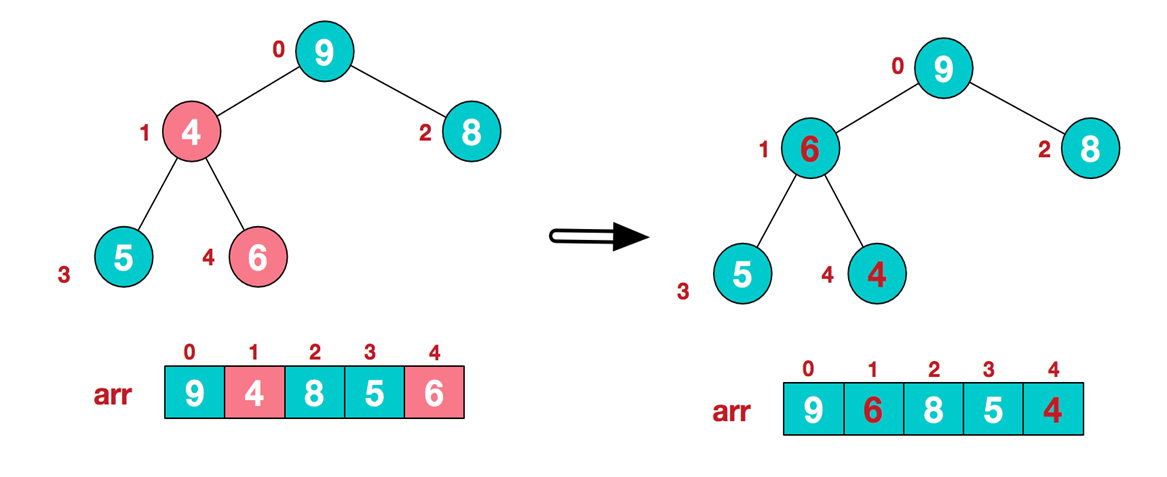
此时,我们就将一个无序序列构造成了一个大顶堆。
步骤二 将堆顶元素与末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换。
-
.将堆顶元素9和末尾元素4进行交换
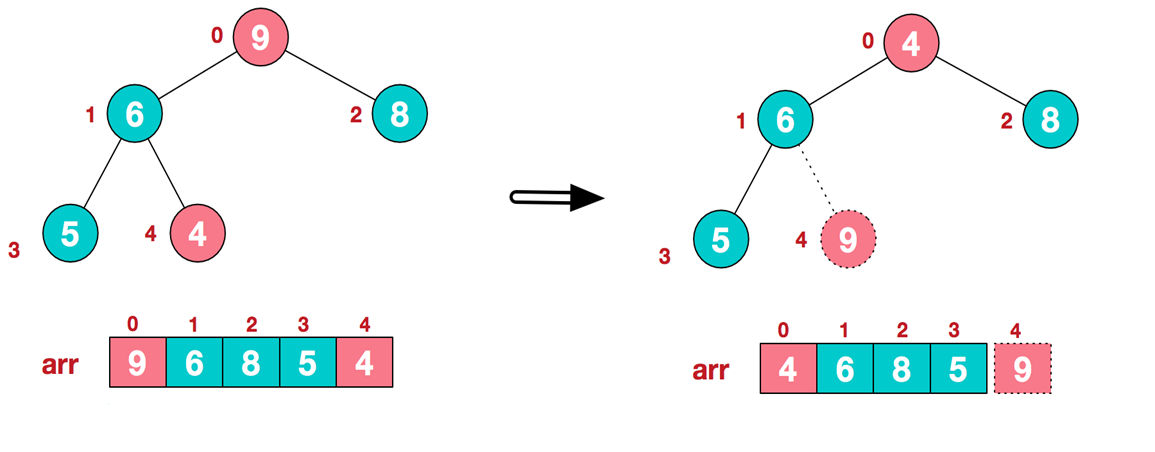
-
.重新调整结构,使其继续满足堆定义

-
.再将堆顶元素8与末尾元素5进行交换,得到第二大元素8.
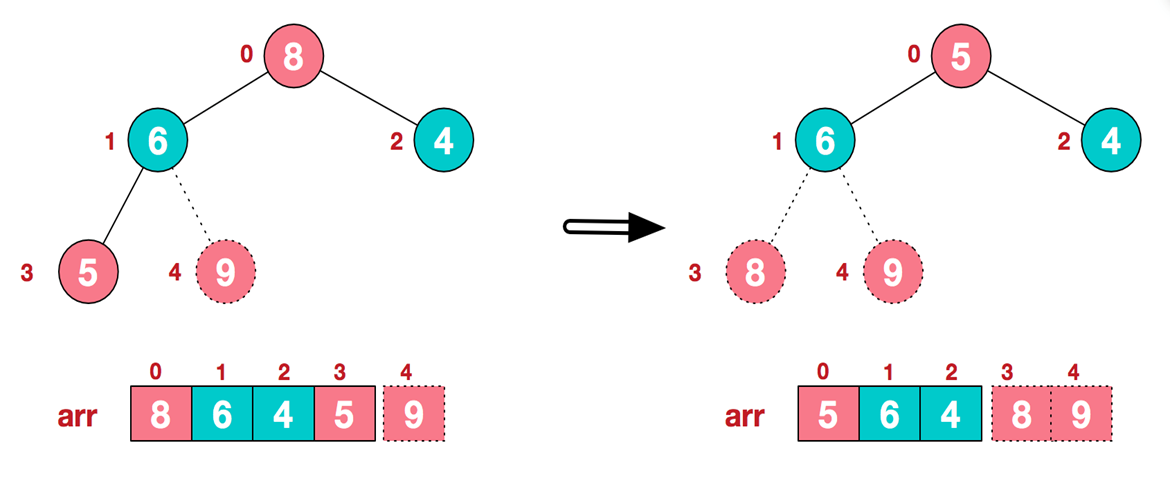
-
后续过程,继续进行调整,交换,如此反复进行,最终使得整个序列有序
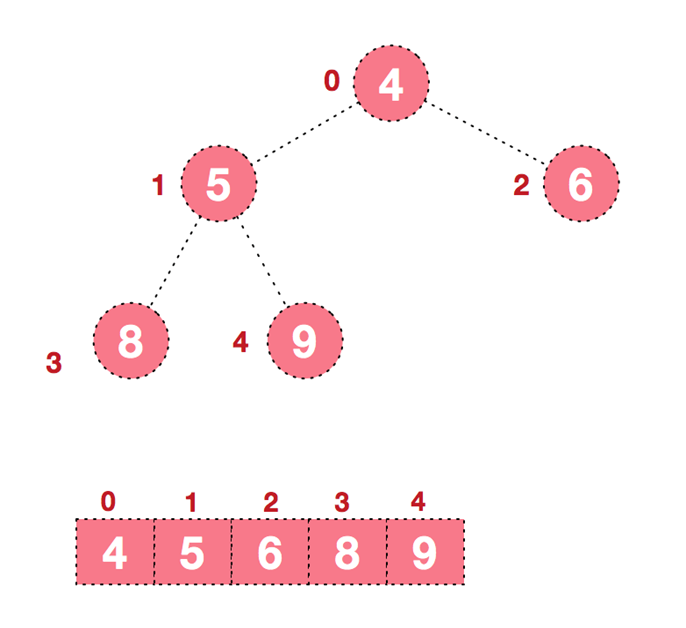
再简单总结下堆排序的基本思路:
1).将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
2).将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
3).重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素, 反复执行调整+交换步骤,直到整个序列有序。
1.1.4 堆排序代码实现
要求:给你一个数组 {4,6,8,5,9} , 要求使用堆排序法,将数组升序排序。
代码实现:
package itcast04;
// 速度: 800000数据排序,3~4秒
import java.text.SimpleDateFormat;
import java.util.Date;public class HeapSort {public static void main(String[] args) {// 要求对数组进行升序排序(大顶堆)
// int arr[] = {4, 6, 8, 5, 9, -1, 90, 89, 56, -999};// 随机创建一个80000个随机数int arr[] = new int[8000000];for(int i = 0; i < 8; i++) {arr[i] = (int)(Math.random()*8000000);//生成一个[0, 800000)}System.out.println("排序前:");Date data1 = new Date();SimpleDateFormat simpleDateFormat = new SimpleDateFormat("yyyy-MM-HH:mm:ss");String date1Str = simpleDateFormat.format(data1);heapSort(arr);Date data2 = new Date();SimpleDateFormat simpleDateFormat2 = new SimpleDateFormat("yyyy-MM-ss");String date2Str = simpleDateFormat2.format(data2);System.out.println("排序前:" + date1Str);System.out.println("排序后:" + date2Str);}// 编写一个堆排序(测试用)public static void heapSort(int arr[]) {int temp = 0;System.out.println("堆排序!!!");// 分布完成
// adjustHeap(arr, 1, arr.length);
// System.out.println("第一次" + Arrays.toString(arr));
//
// adjustHeap(arr, 0, arr.length);
// System.out.println("第二次" + Arrays.toString(arr));// 完成最终的代码for (int i = arr.length / 2 - 1; i >= 0; i--) {adjustHeap(arr, i, arr.length);}//第二部分://2)将无序序列构建为一个堆,根据最大元素沉到数组末端//3)重新调整结构,使其能满足堆定义,然后继续交换堆顶元素与单前末尾元素, 反复执行调整+交换步骤,直到整个序列有序for (int j = arr.length - 1; j > 0; j--) {// 交换temp = arr[j];arr[j] = arr[0];arr[0] = temp;adjustHeap(arr, 0, j);}// System.out.println(Arrays.toString(arr));}// 将一个数组(二叉树),调整成为一个大顶堆/*** aim : 完成将以 i 对应的非叶子节点的数调整为大顶堆* 举例: int arr[] = {4, 6, 8, 5, 9}; => i = 1 => adjustHeap => 得到{4, 9, 8, 5, 6}* 如果我们再次调用adjustHeap 传入的是i= 0 => 得到的是{4, 9, 8, 5, 6} => {9, 6, 8, 5, 4}** @param arr 待调整的数组* @param i 表示非叶子节点在数组中的索引* @param length 表示对多少个元素调整, length是逐渐在减小*/public static void adjustHeap(int arr[], int i, int length) {int temp = arr[i];//开始调整// 说明:// 1. k = i * 2 + 1, k 是i节点的左子节点for (int k = i * 2 + 1; k < length; k = k * 2 + 1) {if (k + 1 < length && arr[k] < arr[k + 1]) {// 说明左子节点的值小于右子节点k++;//指向右子节点}if (arr[k] > temp) {// 如果子节点大于父节点arr[i] = arr[k];// 把较大的值赋给单前节点i = k;// !!! i 指向 k,继续循环比较} else {break;// 这地方为什么我敢直接break, 原因: 我们创建大顶堆的遍历次序(见上)}}// 当for循环结束时,我们已经将以 i 为父节点的树的最大值, 放在了最顶(局部)arr[i] = temp;// 将temp值放在调整后的位置}
}
1.2 赫夫曼树
1.2.1 基本介绍
-
给定n个权值作为n个叶子结点,构造一棵二叉树,若该树的带权路径长度(wpl)达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree), 还有的书翻译为霍夫曼树。
-
赫夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
1.2.2 赫夫曼树几个重要概念和举例说明
-
路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为
L-1。 -
结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
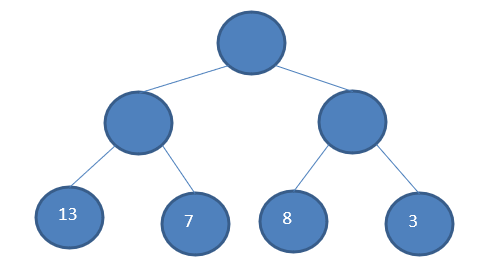
- 树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为
WPL(weighted path length),权值越大的结点离根结点越近的二叉树才是最优二叉树。 - WPL最小的就是赫夫曼树
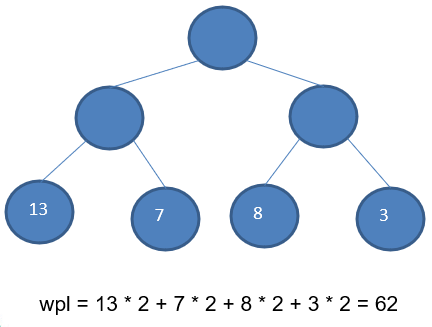
- 树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为
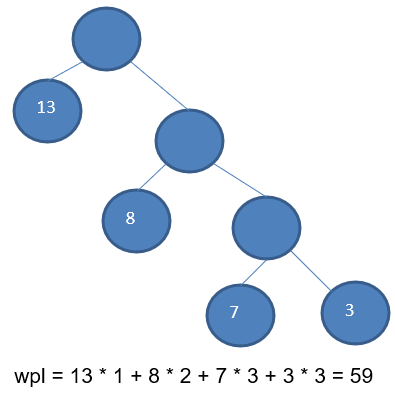
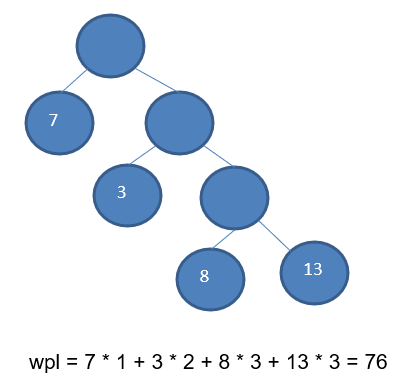
1.2.3 赫夫曼树创建思路图解
给你一个数列 {13, 7, 8, 3, 29, 6, 1},要求转成一颗赫夫曼树.
构成赫夫曼树的步骤:
- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树.
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理,就得到一颗赫夫曼树

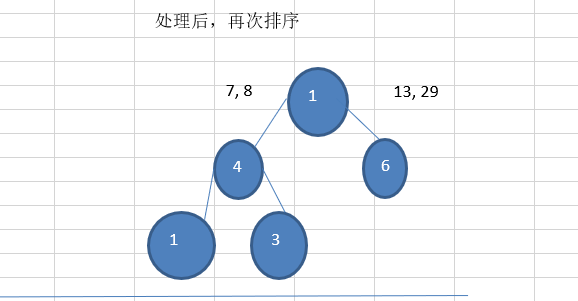
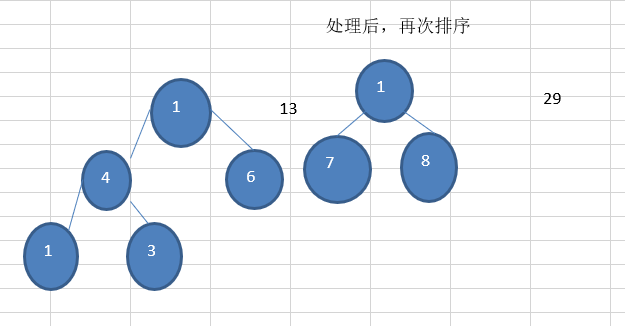
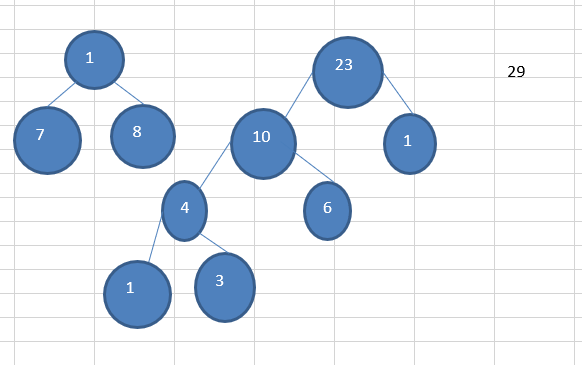
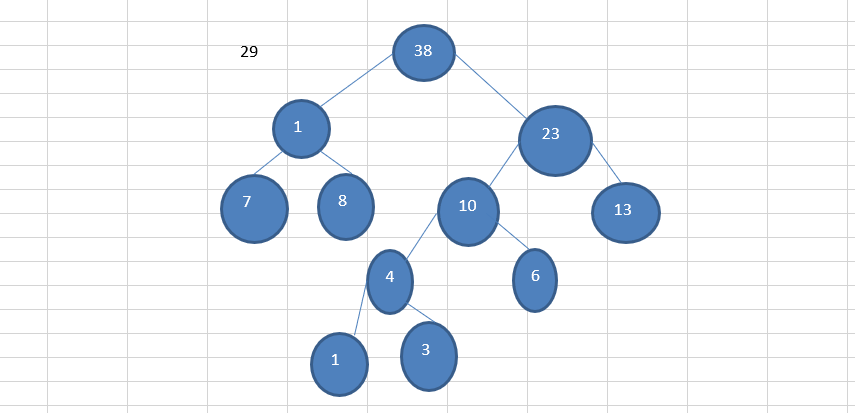
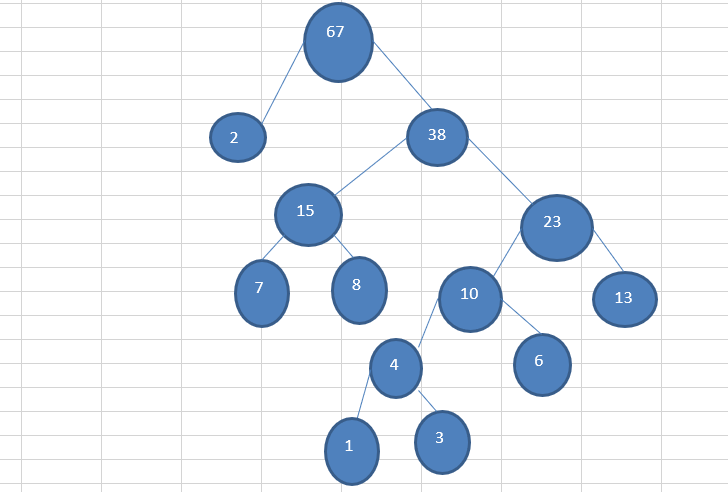
代码实现:
package itcast05;import java.util.ArrayList;
import java.util.Collections;
import java.util.List;public class HuffmanTree {public static void main(String[] args) {int arr[] = {13, 7, 8, 3, 29, 6, 1};Node root = createHuffmanTree(arr);//测试一把(也就是前序遍历一把,看看对不对)preOrder(root);}// 编写一个前序遍历的方法public static void preOrder(Node root) {if(root != null) {root.preOrder();}else {System.out.println("是空树,不能遍历~~~");}}// 创建赫夫曼树的方法/**** @param arr 需要创建成赫夫曼树的数组* @return 返回的创建好的赫夫曼树的root节点*/public static Node createHuffmanTree(int[] arr) {// 1. 为了操作方便,遍历arr数组// 2. 将arr的每一个元素构建成一个Node// 3. 将Node放入到ArrayList中去List<Node> nodes = new ArrayList<Node>();for (int value : arr) {nodes.add(new Node(value));}//我们处理的过程为一个循环的过程while (nodes.size() > 1) {// 排顺序,从小到大,取决于compare函数如何写的Collections.sort(nodes);System.out.println("nodes = " + nodes);// 取出根节点权值最小的;两颗二叉树// (1) 取出权值最小的节点(二叉树)Node leftNode = nodes.get(0);// (2) 取出权值第二小的节点(二叉树)Node rightNode = nodes.get(1);// (3) 构建一颗新的二叉树Node parent = new Node(leftNode.value + rightNode.value);parent.left = leftNode;parent.right = rightNode;// (4) 从ArrayList删除处理过的二叉树nodes.remove(leftNode);nodes.remove(rightNode);// (5) 将parent加入到nodesnodes.add(parent);//System.out.println("第一次处理后:" + nodes);//这里我们需要循环处理}//返回赫夫曼树的root节点return nodes.get(0);}
}//创建节点类
class Node implements Comparable<Node> {int value;// 节点权值Node left;// 指向左子节点Node right;// 指向右子节点// 写个前序遍历public void preOrder() {System.out.println(this);//递归向左子树前序递归if (this.left != null) {this.left.preOrder();}//递归向右子树前序遍历if (this.right != null) {this.right.preOrder();}}public Node(int value) {this.value = value;}public String toString() {return "Node [value = " + value + "]";}public int compareTo(Node o) {// 从小到大排序return this.value - o.value;}
}
1.3 赫夫曼编码
1.4 二叉排序树
1.4.1 常见案例
给你一个数列 (7, 3, 10, 12, 5, 1, 9),要求能够高效的完成对数据的查询和添加。
1.4.2 解决方案分析
使用数组:
数组未排序, 优点:直接在数组尾添加,速度快。 缺点:查找速度慢.
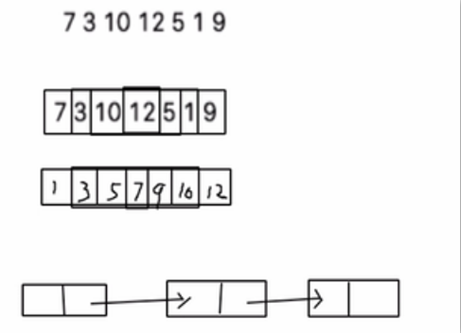
数组排序,优点:可以使用二分查找,查找速度快,缺点:为了保证数组有序,在添加新数据时,找到插入位置后,后面的数据需整体移动,速度慢。
使用链式存储-链表:
不管链表是否有序,查找速度都慢,添加数据速度比数组快,不需要数据整体移动。
使用二叉排序树:
二叉排序树:BST: (Binary Sort(Search) Tree), 对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当前节点的值小,右子节点的值比当前节点的值大。
特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点
比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ,对应的二叉排序树为:
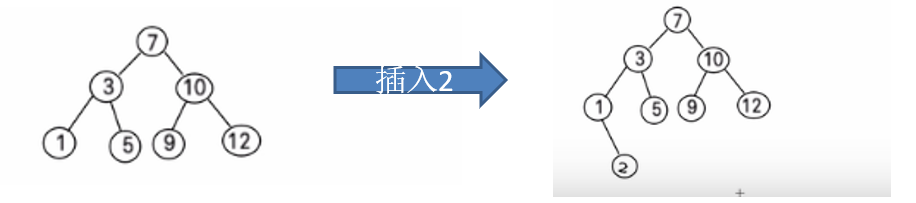
1.4.3 二叉排序树创建和遍历
一个数组创建成对应的二叉排序树,并使用中序遍历二叉排序树,比如: 数组为 Array(7, 3, 10, 12, 5, 1, 9) , 创建成对应的二叉排序树为 :
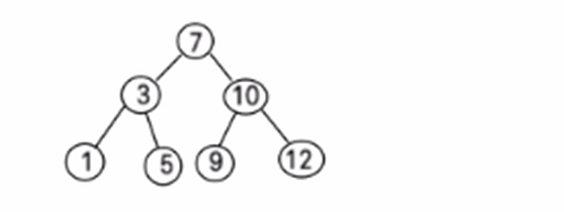
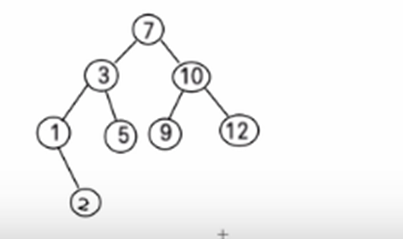
1.4.4 二叉排序树的删除
二叉排序树的删除情况比较复杂,有下面三种情况需要考虑
- 删除叶子节点 (比如:2, 5, 9, 12)
- 删除只有一颗子树的节点 (比如:1)
- 删除有两颗子树的节点. (比如:7, 3,10 )
1.4.5 BST代码实现
package itcast06;// 目标: 课1: 二叉排序树(BST)的创建与增加节点 + 中序遍历
// 课2: 二叉排序树(BST)删除叶子节点
// 课3: 二叉排序树(BST)删除有一颗子树的节点
// 课4: 二叉排序树(BST)删除有两颗子树的节点
public class BinarySortTreeDemo {public static void main(String[] args) {int[] arr = {7, 3, 10, 12, 5, 1, 9, 2};BinarySortTree binarySortTree = new BinarySortTree();// 循环添加节点到for (int i = 0; i < arr.length; i++) {binarySortTree.add(new Node(arr[i]));}// 中序遍历一把// 中序遍历二叉排序树System.out.println("测试中序遍历:");binarySortTree.infixOrder();// 测试删除节点System.out.println("测试删除节点:");
// binarySortTree.delNode(7);binarySortTree.delNode(1);binarySortTree.delNode(2);binarySortTree.delNode(3);binarySortTree.delNode(4);binarySortTree.delNode(5);binarySortTree.delNode(6);binarySortTree.delNode(7);binarySortTree.delNode(9);binarySortTree.delNode(10);binarySortTree.delNode(12);System.out.println("删除节点后:");binarySortTree.infixOrder();}
}// 创建二叉排序树
class BinarySortTree {private Node root;public Node getRoot() {return root;}public void setRoot(Node root) {this.root = root;}// 1. 添加节点方法public void add(Node node) {if (root == null) {root = node;} else {root.add(node);}}// 2. 中序遍历public void infixOrder() {if (root != null) {root.infixOrder();} else {System.out.println("二叉排序树为空,不能遍历。");}}// 3.1 查找要删除的节点public Node search(int value) {if (root == null) {return null;} else {return root.search(value);}}// 3.2 查找父节点public Node searchParent(int value) {if (root == null) {return null;} else {return root.searchParent(value);}}// 编写方法:// 1.返回的 以 node 为根节点的二叉排序树的最小节点的值// 2.删除node 为根节点的二叉排序树的最小节点/**** @param node 传入的节点(当做二叉排序树的根节点)* @return 返回的 以 node 为根节点的二叉排序树的最小节点的值*/public int delRightTreeMin(Node node) {Node target = node;// 循环的查找左子节点,就会找到最小值while(target.left != null) {target = target.left;}// 这时target就指向了最小节点// 删除最小节点delNode(target.value);return target.value;}// 3.3 删除节点public void delNode(int value) {if (root == null) {return;} else {// 1. 需求先去找要删除的节点 targetNodeNode targetNode = search(value);// 可能这个节点不存在, 这个节点没有找到if (targetNode == null) {return;}// 如果我们发现单前这颗二叉排序树只有一个节点if (root.left == null && root.right == null) {root = null;return;// 直接置空就行了}// 去找targetNode的父节点Node parent = searchParent(value);// 如果删除的是叶子节点if (targetNode.left == null && targetNode.right == null) {// 判断targetNode 是父节点的左子节点, 还是右子节点if (parent.left != null && parent.left.value == value) {// 是左子节点parent.left = null;} else if (parent.right != null && parent.right.value == value) {// 是右子节点parent.right = null;}} else if (targetNode.left != null && targetNode.right != null) { // 删除有两颗子树的节点int minVal = delRightTreeMin(targetNode.right);targetNode.value = minVal;} else { // 删除只有一颗子树的节点// 如果要删除的节点有左子节点if (targetNode.left != null) {if(parent != null) {// 如果targetNode 是parent 的左子节点if (targetNode.left.value == value) {parent.left = targetNode.left;} else { // targetNode 是parent 的右子节点parent.right = targetNode.left;}} else {root = targetNode.left;}} else { // 如果要删除的节点有左子节点if (parent != null) {// 如果targetNode 是parent 的左子节点if (parent.left.value == value) {parent.left = targetNode.right;} else {// 如果targetNode 是parent 的右子节点parent.right = targetNode.right;}} else {root = targetNode.right;}}}}}
}// 节点创建
class Node {int value;Node left;Node right;@Overridepublic String toString() {return "Node{" +"value=" + value +", left=" + left +", right=" + right +'}';}public int getValue() {return value;}public void setValue(int value) {this.value = value;}public Node getLeft() {return left;}public void setLeft(Node left) {this.left = left;}public Node getRight() {return right;}public void setRight(Node right) {this.right = right;}public Node(int value) {this.value = value;}// 1. 添加节点的方法// 递归的形式添加节点, 注意需要满足二叉排序树的要求public void add(Node node) {if (node == null) {return;}// 判断传入的节点的值, 和当前的子树的根节点的值比较if (node.value < this.value) {// 如果当前节点左子节点为nullif (this.left == null) {this.left = node;} else {// 递归的向左子树添加this.left.add(node);}} else {// 添加的节点的值大于当前节点的值if (this.right == null) {this.right = node;} else {// 递归的向右子树添加this.right.add(node);}}}// 2. 中序遍历public void infixOrder() {if (this.left != null) {this.left.infixOrder();}System.out.println(this);if (this.right != null) {this.right.infixOrder();}}// 3. 删除节点/*** 第一种情况:* 删除叶子节点 (比如:2, 5, 9, 12)* 思路* (1) 需求先去找到要删除的结点 targetNode* (2) 找到targetNode 的 父结点 parent* (3) 确定 targetNode 是 parent的左子结点 还是右子结点* (4) 根据前面的情况来对应删除* 左子结点 parent.left = null* 右子结点 parent.right = null;* 第二种情况: 删除只有一颗子树的节点 比如 1* 思路* (1) 需求先去找到要删除的结点 targetNode* (2) 找到targetNode 的 父结点 parent* (3) 确定targetNode 的子结点是左子结点还是右子结点* (4) targetNode 是 parent 的左子结点还是右子结点* (5) 如果targetNode 有左子结点* 5. 1 如果 targetNode 是 parent 的左子结点* parent.left = targetNode.left;* 5.2 如果 targetNode 是 parent 的右子结点* parent.right = targetNode.left;* (6) 如果targetNode 有右子结点* 6.1 如果 targetNode 是 parent 的左子结点* parent.left = targetNode.right;* 6.2 如果 targetNode 是 parent 的右子结点* parent.right = targetNode.right*** 情况三 : 删除有两颗子树的节点. (比如:7, 3,10 )* 思路* (1) 需求先去找到要删除的结点 targetNode* (2) 找到targetNode 的 父结点 parent* (3) 从targetNode 的右子树找到最小的结点* (4) 用一个临时变量,将 最小结点的值保存 temp = 11* (5) 删除该最小结点* (6) targetNode.value = temp*/// 3.1 查找要删除的节点/*** @param value 希望删除的节点的值* @return 如果找到,返回该节点;否则,返回null*/public Node search(int value) {if (value == this.value) {// 找到的就是该节点return this;} else if (value < this.value) {// 如果查找的是值小于当前节点, 向左子树递归// 如果左子节点为空if (this.left == null) {return null;}return this.left.search(value);} else {// 如果查找的是值大于当前节点, 向右子树递归if (this.right == null) {return null;}return this.right.search(value);}}// 3.2 查找要删除节点的父节点/*** @param value 要找到节点的值* @return 返回的是要删除的节点的父节点;如果没有,就返回null*/public Node searchParent(int value) {if ((this.left != null && this.left.value == value) ||(this.right != null && this.right.value == value)) {return this;} else {// 如果查找的值小于当前节点的值,并且当前节点的左子节点不为空if (value < this.value && this.left != null) {return this.left.searchParent(value);// 向左子树递归查询} else if (value >= this.value && this.right != null) {return this.right.searchParent(value);} else {return null;}}}
}
1.5 平衡二叉树(AVL树)
看一个案例(说明二叉排序树可能的问题)
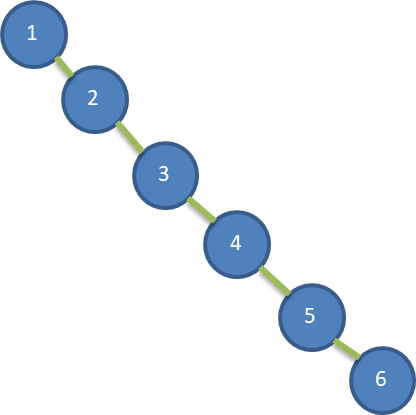
给你一个数列{1,2,3,4,5,6},要求创建一颗二叉排序树(BST), 并分析问题所在.
左边BST 存在的问题分析:
左子树全部为空,从形式上看,更像一个单链表.
插入速度没有影响
查询速度明显降低(因为需要依次比较), 不能发挥BST的优势,因为每次还需要比较左子树,其查询速度比单链表还慢
解决方案-平衡二叉树(AVL) :
1.5.1 基本介绍
- 平衡二叉树也叫平衡二叉搜索树(Self-balancing binary search tree)又被称为AVL树, 可以保证查询效率较高。
- 具有以下特点:它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。
- 举例说明, 看看下面哪些AVL树, 为什么?
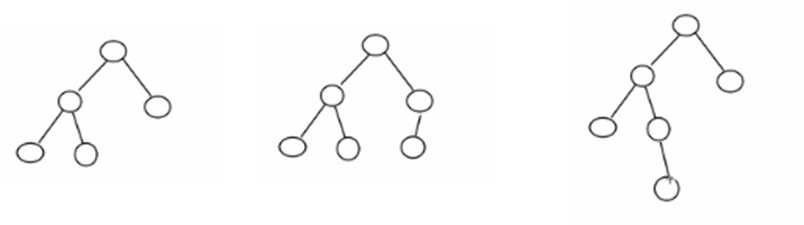
1.5.2 应用案例-单旋转(左旋转)
要求: 给你一个数列,创建出对应的平衡二叉树.数列 {4,3,6,5,7,8}
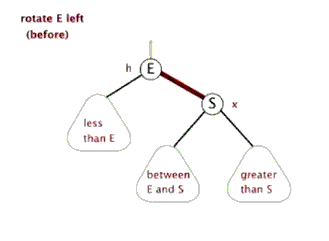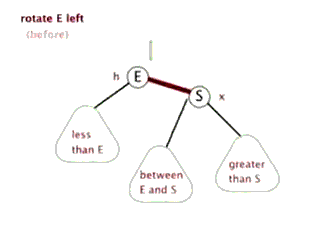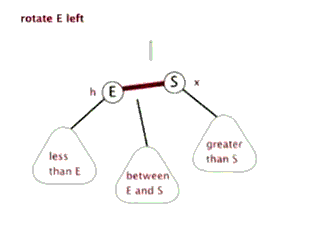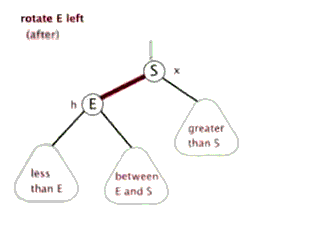
对节点A进行左旋转的步骤
- 将A 节点的 右节点 的 左节点 ,指向 A节点
- 将 A节点的右节点,指向A 节点的右节点的左节点
思路分析(示意图)
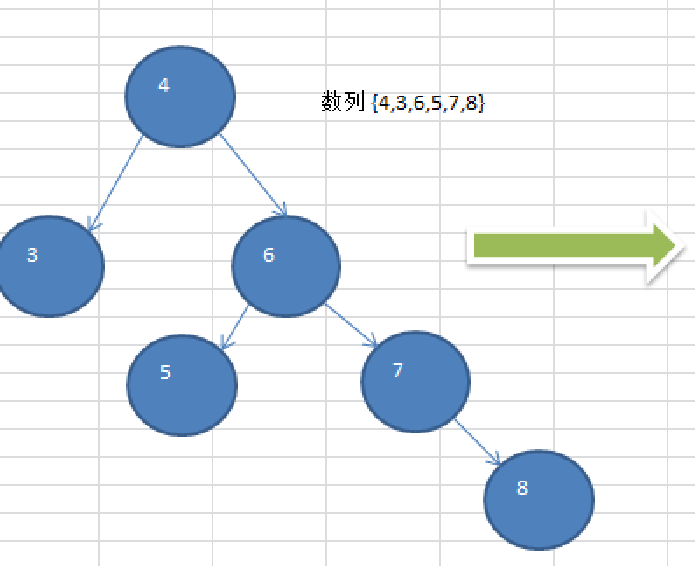

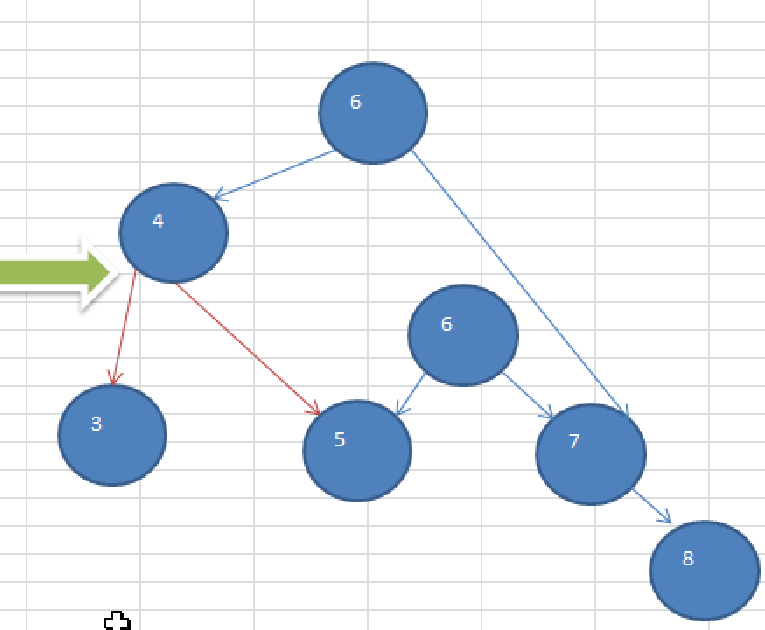
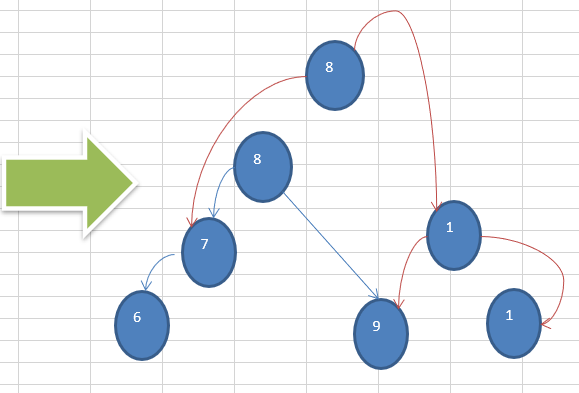
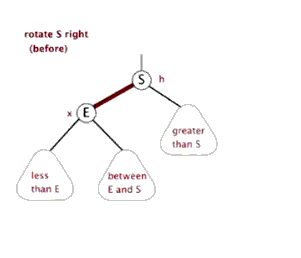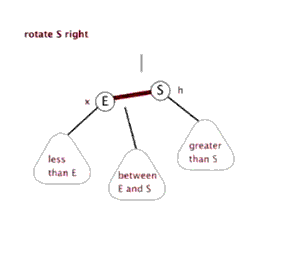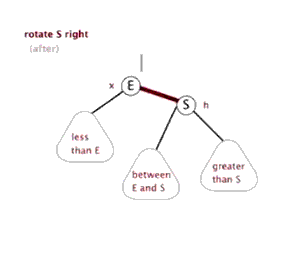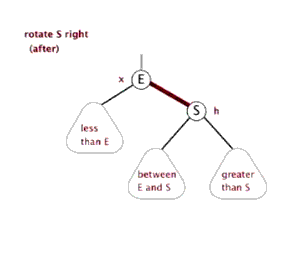
1.5.3 应用案例-单旋转(右旋转)
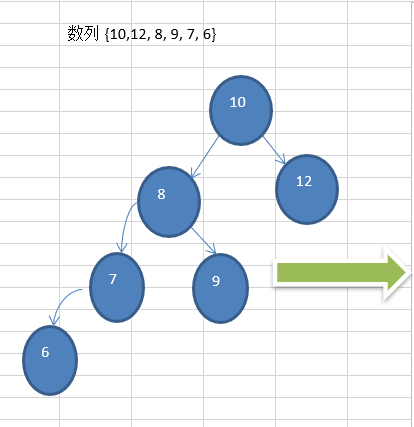
对节点A进行右旋转的步骤
- 将A 节点的 左节点 的 右节点 ,指向 A节点
- 将 A节点的左节点,指向A 节点的左节点的右节点
示意图:

1.5.4 应用案例-双旋转
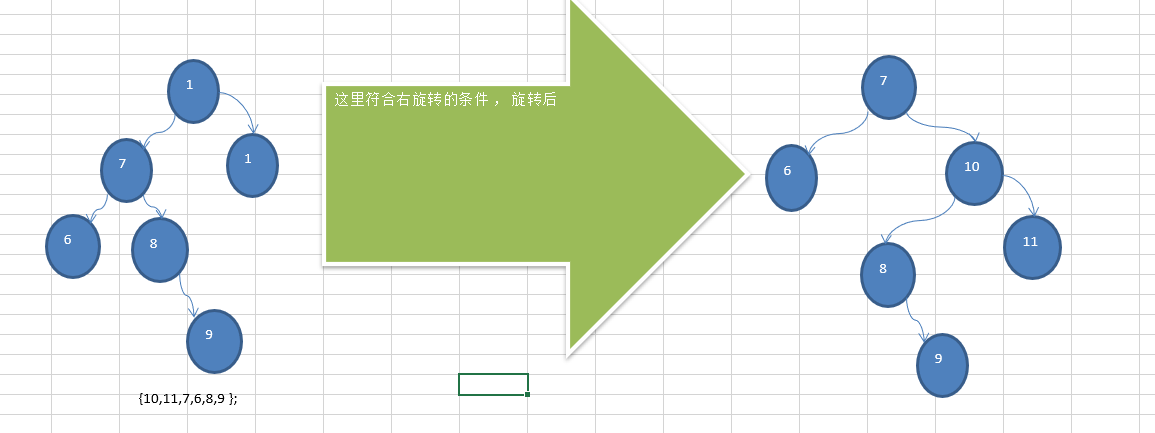
前面的两个数列,进行单旋转(即一次旋转)就可以将非平衡二叉树转成平衡二叉树,但是在某些情况下,单旋转不能完成平衡二叉树的转换。比如数列
int[] arr = { 10, 11, 7, 6, 8, 9 }; 运行原来的代码可以看到,并没有转成 AVL树.
int[] arr = {2,1,6,5,7,3}; // 运行原来的代码可以看到,并没有转成 AVL树
问题分析

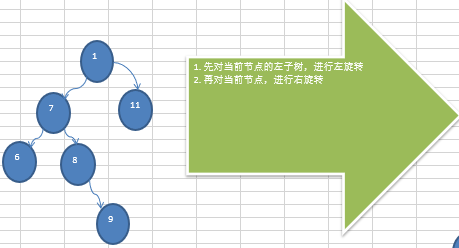
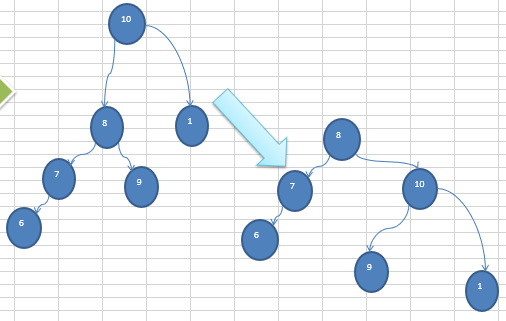
1.5.5 代码实现
package itcast07;public class AVLTreeDemo {public static void main(String[] args) {int[] arr = {4, 3, 6, 5, 7, 8};int[] arr1 = {10, 11, 7, 6, 8, 9};// 创建一个AVLTree对象AVLTree avlTree = new AVLTree();// 添加节点for(int i = 0; i < arr.length; i++) {avlTree.add(new Node(i));}// 再创建一个AVLTree对象AVLTree avlTree1 = new AVLTree();// 添加节点for(int i = 0; i < arr1.length; i++) {avlTree.add(new Node(i));}// 遍历System.out.println("中序遍历");avlTree.infixOrder();System.out.println("avlTree 在没有平衡处理前~~~");System.out.println("树的高度是:"+ avlTree.getRoot().height());// 4System.out.println("树的左子树的高度:" + avlTree.getRoot().leftHeight());// 1System.out.println("树的右子树的高度:" + avlTree.getRoot().leftHeight());// 3// 右子树高度 > 左子树高度, 所以要进行左旋转System.out.println("avlTree1 在没有平衡处理前~~~");// 这个地方需要在回看P 140System.out.println("树的高度是:"+ avlTree1.getRoot().height());//System.out.println("树的左子树的高度:" + avlTree1.getRoot().leftHeight());//System.out.println("树的右子树的高度:" + avlTree1.getRoot().leftHeight());//}
}
/*
如果当前右子树的节点高度大于左子树的高度
那么需要进行左旋转,将排序二叉树,变为AVL树*/
/*
左旋转的变法:
问题:当插丸8时
rightHeight()- leftHeight()> 1成立·此时·不再是—果avl树了.
怎么处理--进行左旋转.
1.创建一个新的节点newNode (以4这个值创建),创建一个新的节点,值等于当前根节点的值
// 把新节点的左子树设置了当前节点的左子树
2.newNode.left = left
// 把新节点的右子树设置为当前节点的右子树的左子树
3.newNode.right =right.left;把当前节点的值换为右子节点的值
4.value=right.value;
// 把当前节点的右子树设置成右子树的右子树
5.right=right.right;把当前节点的左子树设置为新节点
6.left=newLeft;
注:根据java的垃圾回收机制。如果值没有引用指向时, 那么就会被收回。*/// 创建AVL树
class AVLTree {private Node root;public Node getRoot() {return root;}public void setRoot(Node root) {this.root = root;}// 1. 添加节点方法public void add(Node node) {if (root == null) {root = node;} else {root.add(node);}}// 2. 中序遍历public void infixOrder() {if (root != null) {root.infixOrder();} else {System.out.println("二叉排序树为空,不能遍历。");}}// 3.1 查找要删除的节点public Node search(int value) {if (root == null) {return null;} else {return root.search(value);}}// 3.2 查找父节点public Node searchParent(int value) {if (root == null) {return null;} else {return root.searchParent(value);}}// 编写方法:// 1.返回的 以 node 为根节点的二叉排序树的最小节点的值// 2.删除node 为根节点的二叉排序树的最小节点/*** @param node 传入的节点(当做二叉排序树的根节点)* @return 返回的 以 node 为根节点的二叉排序树的最小节点的值*/public int delRightTreeMin(Node node) {Node target = node;// 循环的查找左子节点,就会找到最小值while (target.left != null) {target = target.left;}// 这时target就指向了最小节点// 删除最小节点delNode(target.value);return target.value;}// 3.3 删除节点public void delNode(int value) {if (root == null) {return;} else {// 1. 需求先去找要删除的节点 targetNodeNode targetNode = search(value);// 可能这个节点不存在, 这个节点没有找到if (targetNode == null) {return;}// 如果我们发现单前这颗二叉排序树只有一个节点if (root.left == null && root.right == null) {root = null;return;// 直接置空就行了}// 去找targetNode的父节点Node parent = searchParent(value);// 如果删除的是叶子节点if (targetNode.left == null && targetNode.right == null) {// 判断targetNode 是父节点的左子节点, 还是右子节点if (parent.left != null && parent.left.value == value) {// 是左子节点parent.left = null;} else if (parent.right != null && parent.right.value == value) {// 是右子节点parent.right = null;}} else if (targetNode.left != null && targetNode.right != null) { // 删除有两颗子树的节点int minVal = delRightTreeMin(targetNode.right);targetNode.value = minVal;} else { // 删除只有一颗子树的节点// 如果要删除的节点有左子节点if (targetNode.left != null) {if (parent != null) {// 如果targetNode 是parent 的左子节点if (targetNode.left.value == value) {parent.left = targetNode.left;} else { // targetNode 是parent 的右子节点parent.right = targetNode.left;}} else {root = targetNode.left;}} else { // 如果要删除的节点有左子节点if (parent != null) {// 如果targetNode 是parent 的左子节点if (parent.left.value == value) {parent.left = targetNode.right;} else {// 如果targetNode 是parent 的右子节点parent.right = targetNode.right;}} else {root = targetNode.right;}}}}}
}// 节点创建
class Node {int value;Node left;Node right;@Overridepublic String toString() {return "Node{" +"value=" + value +", left=" + left +", right=" + right +'}';}public int getValue() {return value;}public void setValue(int value) {this.value = value;}public Node getLeft() {return left;}public void setLeft(Node left) {this.left = left;}public Node getRight() {return right;}public void setRight(Node right) {this.right = right;}public Node(int value) {this.value = value;}// 1. 添加节点的方法// 递归的形式添加节点, 注意需要满足二叉排序树的要求public void add(Node node) {if (node == null) {return;}// 判断传入的节点的值, 和当前的子树的根节点的值比较if (node.value < this.value) {// 如果当前节点左子节点为nullif (this.left == null) {this.left = node;} else {// 递归的向左子树添加this.left.add(node);}} else {// 添加的节点的值大于当前节点的值if (this.right == null) {this.right = node;} else {// 递归的向右子树添加this.right.add(node);}}//当添加完一个节点后, 如果右子树的高度 - 左子树的高度 > 1, 左旋转if(rightHeight() - leftHeight() > 1) {// 如果它的右子树的左子树的高度大于它的右子树的高度if(right != null && right.leftHeight() > right.rightHeight()) {// 先对右子节点进行右旋转right.rightRotate();// 然后在对当前节点进行左旋转leftRotate();// 左旋转} else {// 直接进行左旋转即可leftRotate();}return;// 必须要。防止重复处理}// 当添加完一个节点后, 如果左子树的高度 - 右子树的高度 > 1, 右旋转if(leftHeight() - rightHeight() > 1) {// 如果他的左子树的右子树高度大于它的左子树的高度if(left != null && left.rightHeight() > left.leftHeight()) {// 先对当前节点的左节点(左子树) -> 左旋转left.leftRotate();// 再对单前节点的进行右旋转rightRotate();} else {// 直接进行右旋转即可rightRotate();}rightRotate();// 右旋转}}// 2. 中序遍历public void infixOrder() {if (this.left != null) {this.left.infixOrder();}System.out.println(this);if (this.right != null) {this.right.infixOrder();}}// 返回单前节点的高度, 以该节点为根节点的树的高度public int height() {return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;}// 返回左子树的高度public int leftHeight() {if (left == null) {return 0;}return left.height();}// 返回右子树的高度public int rightHeight() {if (right == null) {return 0;}return right.height();}// 左旋转方法private void leftRotate() {// 创建新的节点, 以当前的根节点的值Node newNode = new Node(value);// 把新的节点左子树设置成为当前节点的左子树newNode.left = left;// 把新的节点的右子树设置成单前节点右子树的左子树newNode.right = right.left;// 把单前节点的值替换右子节点的值value = right.value;// 把当前节点右子树设置成为单前节点的右子树的右子树right = right.right;// 把当前节点的的左子树(左子节点)设置成新的节点left = newNode;}// 右旋转private void rightRotate() {Node newNode = new Node(value);newNode.right = right;newNode.left = left.right;value = left.value;left = left.left;right = newNode;}// 3. 删除节点// 3.1 查找要删除的节点/*** @param value 希望删除的节点的值* @return 如果找到,返回该节点;否则,返回null*/public Node search(int value) {if (value == this.value) {// 找到的就是该节点return this;} else if (value < this.value) {// 如果查找的是值小于当前节点, 向左子树递归// 如果左子节点为空if (this.left == null) {return null;}return this.left.search(value);} else {// 如果查找的是值大于当前节点, 向右子树递归if (this.right == null) {return null;}return this.right.search(value);}}// 3.2 查找要删除节点的父节点/*** @param value 要找到节点的值* @return 返回的是要删除的节点的父节点;如果没有,就返回null*/public Node searchParent(int value) {if ((this.left != null && this.left.value == value) ||(this.right != null && this.right.value == value)) {return this;} else {// 如果查找的值小于当前节点的值,并且当前节点的左子节点不为空if (value < this.value && this.left != null) {return this.left.searchParent(value);// 向左子树递归查询} else if (value >= this.value && this.right != null) {return this.right.searchParent(value);} else {return null;}}}
}








