您现在的位置是:主页 > news > 广州推广型网站建设/怎么设计一个网页
广州推广型网站建设/怎么设计一个网页
![]() admin2025/5/5 1:55:52【news】
admin2025/5/5 1:55:52【news】
简介广州推广型网站建设,怎么设计一个网页,做网站出路,建设部网站官网施工合同文本2021-11-11每日刷题打卡 力扣——二叉搜索树 538. 把二叉搜索树转换为累加树和1038. 把二叉搜索树转换为累加树和剑指 Offer II 054. 所有大于等于节点的值之和 给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Grea…
2021-11-11每日刷题打卡
力扣——二叉搜索树
538. 把二叉搜索树转换为累加树和1038. 把二叉搜索树转换为累加树和剑指 Offer II 054. 所有大于等于节点的值之和
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
节点的左子树仅包含键 小于 节点键的节点。
节点的右子树仅包含键 大于 节点键的节点。
左右子树也必须是二叉搜索树。
注意:本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同
示例 1:
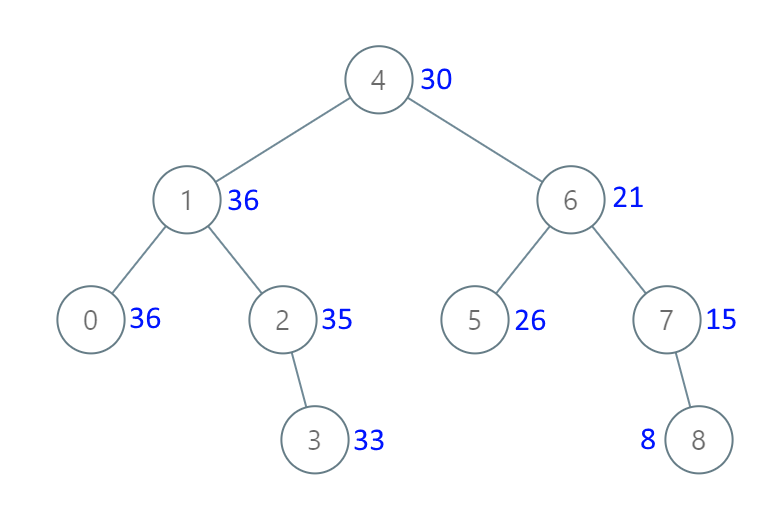
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
准备一个vector容器v,然后对root中序遍历,每遍历到一个节点时,先用这个节点的值对v中所有元素相加,然后再把这个节点的值插入v中,这样最好得到的是所有大于等于当前节点的和了,再遍历一遍root,把节点值用v中的值替换掉即可。
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<int>v;TreeNode* convertBST(TreeNode* root) {dfs(root);int i=0;dfs2(root,i);return root;}void dfs(TreeNode* root){if(!root)return;dfs(root->left);for(int& i:v)i+=root->val;v.push_back(root->val);dfs(root->right);}void dfs2(TreeNode*& root,int& i){if(!root)return;dfs2(root->left,i);root->val=v[i++];dfs2(root->right,i);}
};
剑指 Offer 33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/ \
2 6
/
1 3
示例 1:
输入: [1,6,3,2,5]
输出: false
后序遍历的特点是:[左子树] [右子树] [根节点],所以可知根节点是最后一位,然后左子树总比根节点小,右子树总比根节点大,所以我们在遍历 postorder时可以准备两个vector容器v1、v2来分别存左子树和右子树的节点值(顺便要提前判断一下postorder的size,如果小于等于1,说明必是一个后序遍历,返回true),开始遍历 postorder,把前面遍历到的所有小于根节点的值存入v1中,当遇到第一个大于根节点的值时停止插入v1,而后所有的值都插入v2,这个过程中也要比较,如果有存在小于根节点的值,说明这不是一个合格的二叉搜索数的后序序列,直接返回false,如果一直遍历到结尾也没问题,那么就进行下一次递归,把v1和v2分别送去递归,当所有递归结束后,我们就得到了bool类型的结果。
class Solution {
public:bool flag;bool verifyPostorder(vector<int>& postorder) {return dfs(postorder);}bool dfs(vector<int>&v){int n=v.size();if(n<=1)return true;int j=0;vector<int>v1;vector<int>v2;for(int i=0;i<n;i++){if(v[i]>=v[n-1]){j=i;break;}v1.push_back(v[i]);}for(int i=j;i<n-1;i++){if(v[i]<v[n-1]){return false;}elsev2.push_back(v[i]);}return dfs(v1)&&dfs(v2);}
};
AcWing——算法基础
788. 逆序对的数量 - AcWing题库
给定一个长度为 n 的整数数列,请你计算数列中的逆序对的数量。
逆序对的定义如下:对于数列的第 i 个和第 j 个元素,如果满足 i<j 且 a[i]>a[j],则其为一个逆序对;否则不是。
输入格式
第一行包含整数 nn,表示数列的长度。
第二行包含 nn 个整数,表示整个数列。
输出格式
输出一个整数,表示逆序对的个数。
数据范围
1≤n≤100000
数列中的元素的取值范围 [1,1^9][1,109]。
输入样例:
6
2 3 4 5 6 1
输出样例:
5
这题用的是归并排序来解,你可能有点不理解为什么是归并,这里举个例子。比如有一个序列 15 4 2 3 6,我们最后一步归并会把它变成
1 4 5 |(mid)| 2 3 6 然后比较左右两边的序列,把小的存到数组里,对比1和2,1小,不构成逆序对;然后对比4和2,2小,此时在左边的数组里,因为4右边的数都比4大,所以2能和4以及4右边的全部数组成逆序对,逆序对的数量就为mid-4的下标+1,然后对比4和3……所以我们可以利用归并来求得逆序对的数量,当左边的数组小时我们不多做操作,右边的小时逆序对的数量要加上mid-左边数组当前索引+1。
#include<iostream>
using namespace std;
const int N=1e6+5;
int n;
long long res=0;
int arr[N],tmp[N];void merge_sort(int l,int r)
{if (l >= r)return;int mid = (l + r) / 2;merge_sort(l, mid);merge_sort(mid + 1, r);int i = l, j = mid + 1, k = 0;while (i <= mid && j <= r){if (arr[i] <= arr[j])tmp[k++] = arr[i++];else{tmp[k++] = arr[j++];res += mid - i + 1;}}while (i <= mid)tmp[k++] = arr[i++];while (j <= r)tmp[k++] = arr[j++];for (int i = l, j = 0; i <= r; i++, j++)arr[i] = tmp[j];}int main()
{scanf("%d",&n);for(int i=0;i<n;i++)scanf("%d",&arr[i]);merge_sort(0,n-1);cout<<res;return 0;
}
789. 数的范围 - AcWing题库
给定一个按照升序排列的长度为 n 的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 00 开始计数)。
如果数组中不存在该元素,则返回 -1 -1。
输入格式
第一行包含整数 n 和 q,表示数组长度和询问个数。
第二行包含 n 个整数(均在 1∼100001∼10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1 -1。
数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例:
3 4
5 5
-1 -1
二分查找,查找两次,第一次找数的起始位,第二次找数的终止位
#include<iostream>
using namespace std;
const int N=100010;
int n,m;
int nums[N];
int main()
{scanf("%d%d",&n,&m);for(int i=0;i<n;i++)scanf("%d",&nums[i]);while(m--){int x;scanf("%d",&x);int l=0,r=n-1;int mid=(l+r)/2;while(l<r){if(nums[mid]>=x)r=mid;else l=mid+1;mid=(l+r)/2;}if(nums[l]!=x){cout<<"-1 -1"<<endl;continue;}elsecout<<l<<" ";l=0,r=n-1;mid=(l+r+1)/2;while(l<r){if(nums[mid]<=x)l=mid;else r=mid-1;mid=(l+r+1)/2;}cout<<l<<endl;}return 0;
}








