您现在的位置是:主页 > news > 慈溪企业网站建设/重庆快速排名优化
慈溪企业网站建设/重庆快速排名优化
![]() admin2025/5/2 17:04:47【news】
admin2025/5/2 17:04:47【news】
简介慈溪企业网站建设,重庆快速排名优化,网站的整体风格,西安个人做企业网站目录n的阶乘 (清华上机)题目描述代码汉诺塔问题题目:代码:Fibonacci数列 (上交复试)题目代码:二叉树:题目:代码:n的阶乘 (清华上机) …
目录
- n的阶乘 (清华上机)
- 题目描述
- 代码
- 汉诺塔问题
- 题目:
- 代码:
- Fibonacci数列 (上交复试)
- 题目
- 代码:
- 二叉树:
- 题目:
- 代码:
n的阶乘 (清华上机)
不敢相信这是清华上机
题目描述
输入一个整数n,输出n的阶乘
代码
递归写法:
#include <cstido>
Factorial(int n){if(n==1){return 1;}else{return Factorial(n-1)*n;}
} int main(){int n;scanf("%d",&n);printf("%d\n",Factorial(n));
}
循环写法
int main(){int n;int sum = 1;scanf("%d",&n);for(int i=1;i<=n;i++){sum = sum*i;}printf("%d",sum);
}
汉诺塔问题
题目:
约19世纪末,在欧州的商店中出售一种智力玩具,在一块铜板上有三根杆,最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到右边的杆上,条件是一次只能移动一个盘,且不允许大盘放在小盘的上面。
现在我们改变游戏的玩法,不允许直接从最左(右)边移到最右(左)边(每次移动一定是移到中间杆或从中间移出),也不允许大盘放到下盘的上面。
Daisy已经做过原来的汉诺塔问题和汉诺塔II,但碰到这个问题时,她想了很久都不能解决,现在请你帮助她。现在有N个圆盘,她至少多少次移动才能把这些圆盘从最左边移到最右边?
Input
包含多组数据,每次输入一个N值(1<=N=35)。
Output
对于每组数据,输出移动最小的次数。
Sample Input
1
3
12
Sample Output
2
26
531440
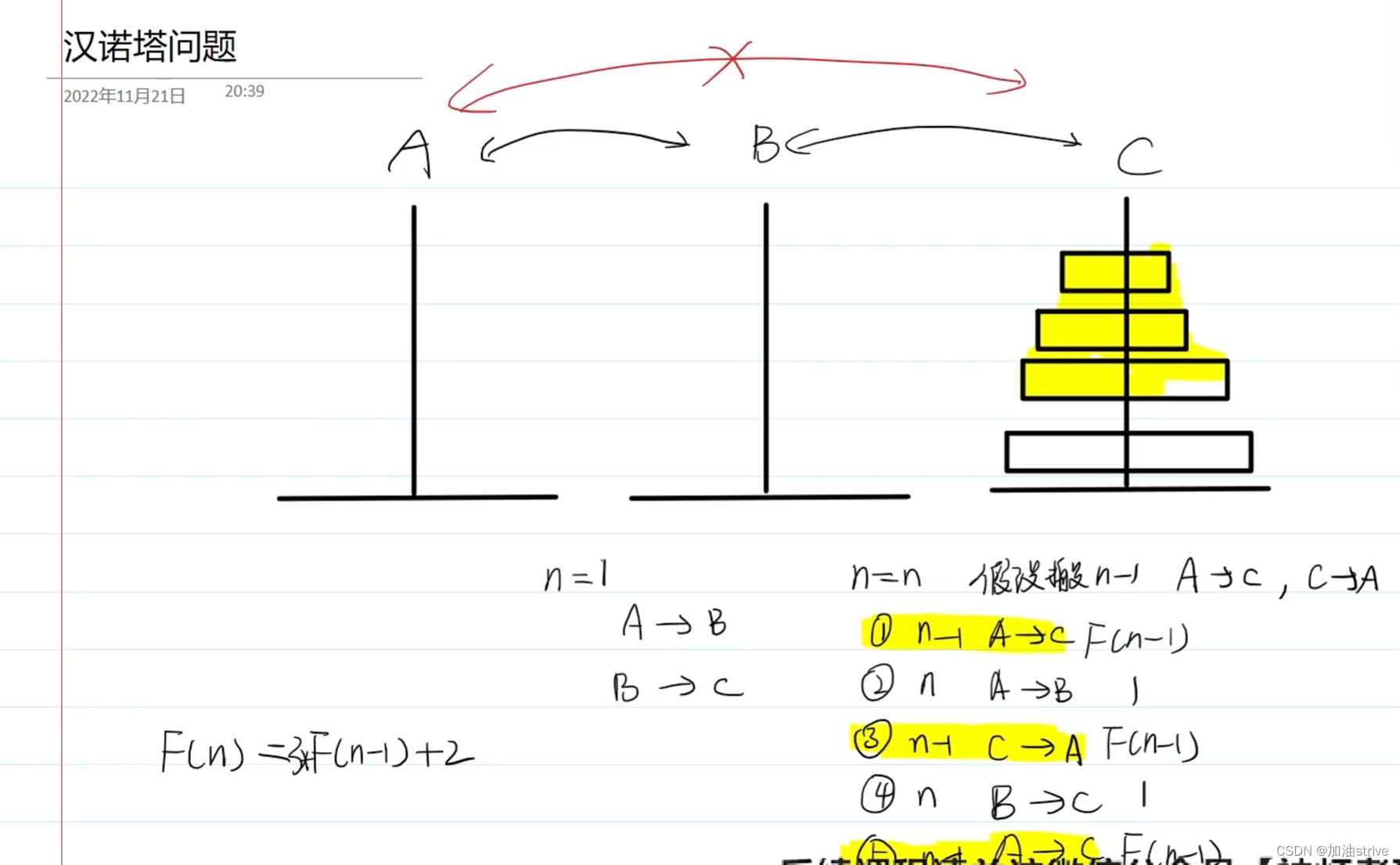
代码:
#include <cstdio>
//现在有N个圆盘,她至少多少次移动才能把这些圆盘从最左边移到最右边?
long long hanoi(int n){if(n==1) return 2;else return 3*hanoi(n-1)+2;
}int main(){int n;while(scanf("%d",&n)!=EOF){printf("%lld",hanoi(n));}
}
Fibonacci数列 (上交复试)
题目
描述
The Fibonacci Numbers{0,1,1,2,3,5,8,13,21,34,55…} are defined by the recurrence: F0=0 F1=1 Fn=Fn-1+Fn-2,n>=2 Write a program to calculate the Fibonacci Numbers.
输入描述:
Each case contains a number n and you are expected to calculate Fn.(0<=n<=30) 。
输出描述:
For each case, print a number Fn on a separate line,which means the nth Fibonacci Number.
示例1
输入:
1
输出:
1
代码:
#include <cstdio>int Fibonacci(int n){if(n==1){return 1;}else if(n==0){return 0;}else{return Fibonacci(n-1)+Fibonacci(n-2);}
}//斐波那契数列
int main(){int n;while(scanf("%d",&n)!=EOF){printf("%d\n",Fibonacci(n));}
}
二叉树:
题目:
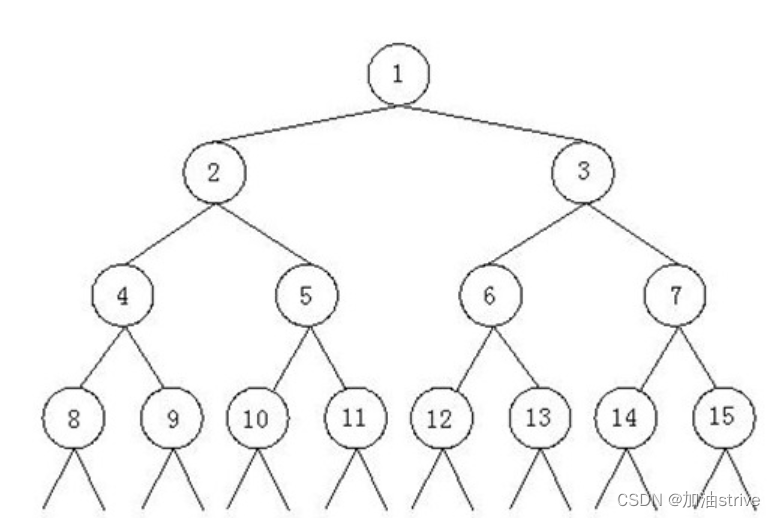
如上所示,由正整数1,2,3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是,结点m所在的子树中一共包括多少个结点。 比如,n = 12,m = 3那么上图中的结点13,14,15以及后面的结点都是不存在的,结点m所在子树中包括的结点有3,6,7,12,因此结点m的所在子树中共有4个结点。
输入描述:
输入数据包括多行,每行给出一组测试数据,包括两个整数m,n (1 <= m <= n <= 1000000000)。
输出描述:
对于每一组测试数据,输出一行,该行包含一个整数,给出结点m所在子树中包括的结点的数目。
示例1
输入:
3 12
0 0
输出:
4
分析:
- 首先:该树是一颗完全二叉树,若root节点是数字p,那么左节点是数字2p
右节点是数字2p+1; - 如果子树存在 tree(m) = tree(2m)+tree(2m+1);
也就是说,该子树的节点数量= 左子树节点数量+右子树节点数量 +1(根节点) - 如果子树根不存在,则tree(m)为0;
代码:
#include <cstdio>// m表示当前节点 n表示节点总数
int tree(int m,int n){// 如果当前节点的序号大于节点总数 if(m > n){return 0;}else{return 1+tree(2*m,n)+tree(2*m+1,n);}
}int main(){int m,n;while(scanf("%d%d",&m,&n)!=EOF){if(m==0) break;printf("%d\n",tree(m,n));}
}







