十大排序算法
- 十大排序算法
- 简单的排序算法
- 插入排序
- 冒泡排序
- 选择排序
- 高效的比较排序算法
- 希尔排序
- 快速排序
- 归并排序
- 堆排序
- 牺牲空间的线性排序算法
- 计数排序
- 桶排序
- 基数排序
- 综合分析
- 简单的排序算法
简单的排序算法
Θ(n^2)
插入排序
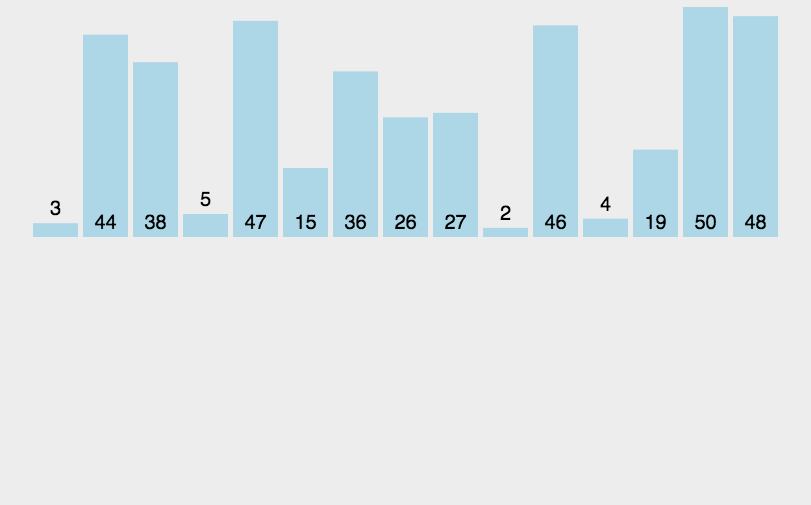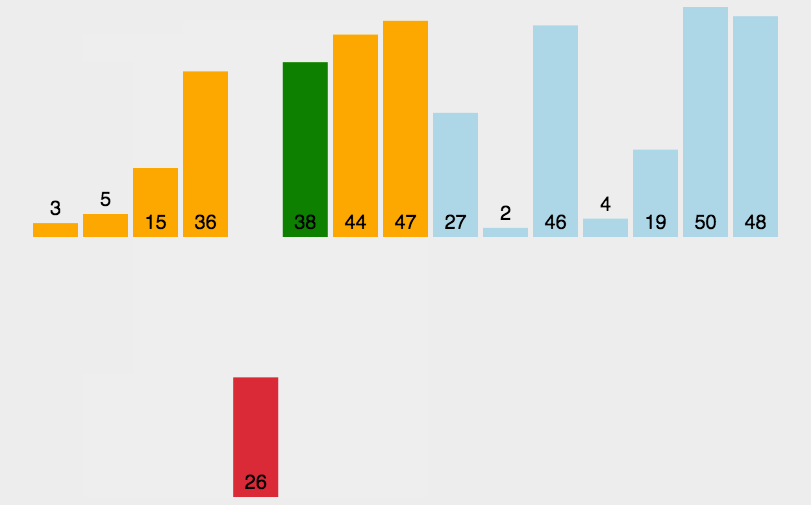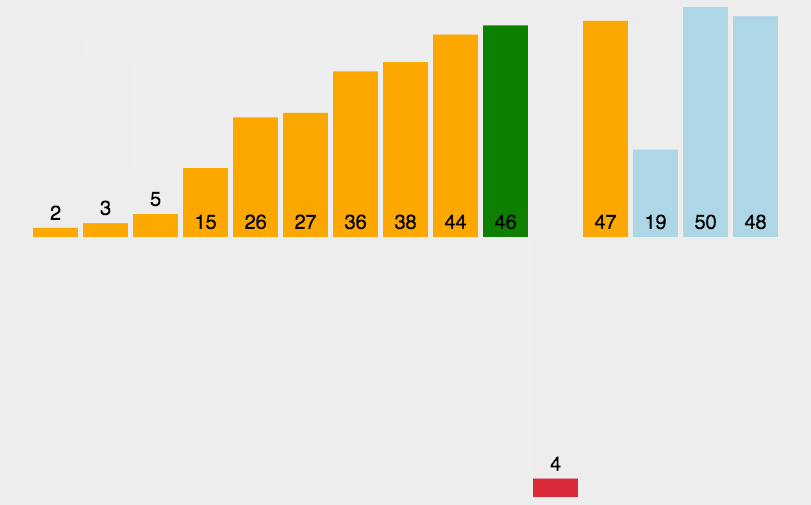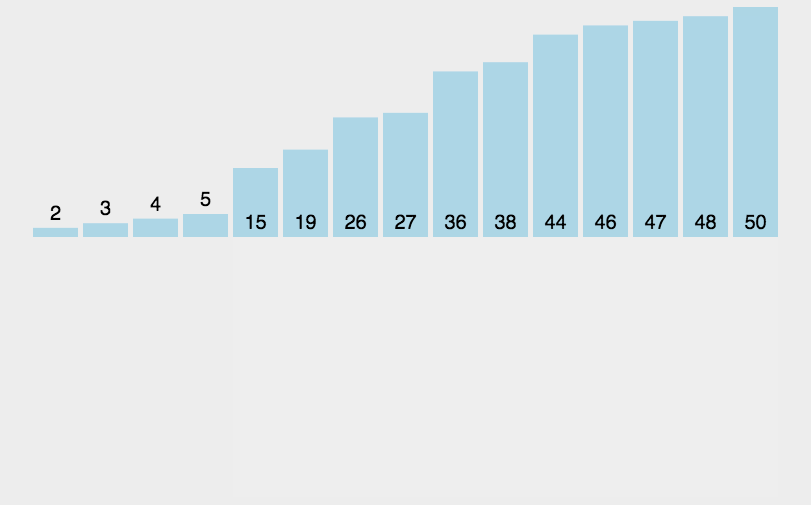
- 动画演示
-
原理
将数组看成两部分,一部分为已排序好的数组,后面的部分为未排序数组,每次从后面的数组中取出元素与前面的有序元素一一比较,若小于则向前移动,直到找到正确的位置插入。遍历后面的数组直到整个数组排序完成。
-
代码
// 准备工作,交换函数 public static void exc(int[] a,int i, int j) {if (a[i]!=a[j]) {a[i]^=a[j];a[j]^=a[i];a[i]^=a[j];}} // 插入排序 public static void insertSort(int[] a, int n) {for (int i = 1; i < n; i++) {for (int j = i; j>0&&a[j-1]>a[j]; j--) {exc(a, j, j-1);}}} -
分析
时间复杂度
- 平均: n×n/4 次比较,n×n/4 次交换
- 最好: n-1 次比较,0次交换
- 最坏: n×n/2 次比较, n×n/2 交换
评价:
插入排序与数组的逆序度有关,最好情况为 O(n),所以经常与快速排序一起出现,详见C语言的quickSort的实现
冒泡排序
-
动画演示
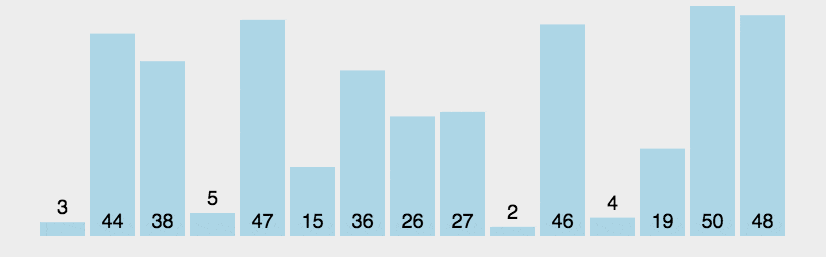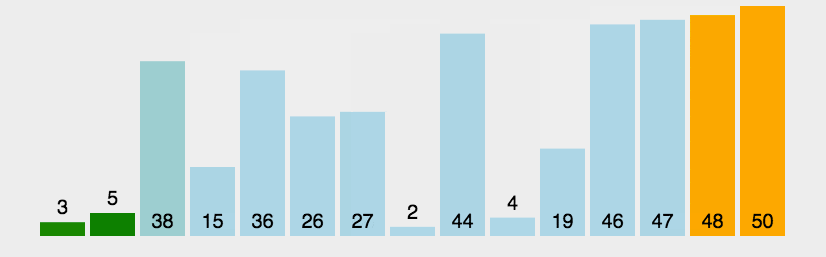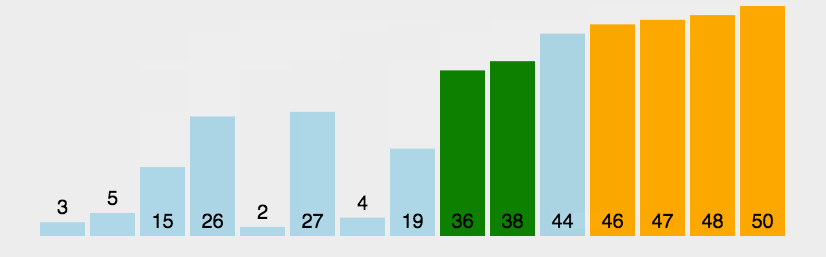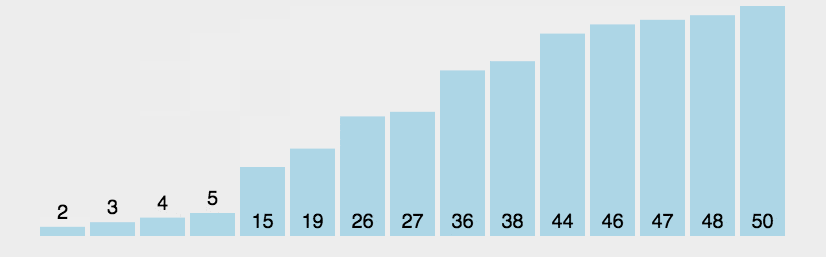
-
原理
就像泡泡一样,不断把大的数字往上浮,遍历完整个数组排序即完成。
-
代码
public static void bubbleSort(int[] a, int n) {boolean flag = true;for (int i = 0; i < n-1&&flag; i++) {flag = false;for (int j = 0; j < n-i-1; j++) {if (a[j]>a[j+1]) {exc(a, j, j+1);flag=true;}}}} -
分析
时间复杂度:
- 平均情况下:冒泡比较的次数约是插入排序的两倍,移动次数一致。
- 平均情况下: 冒泡比较的次数与选择排序是一样的,移动次数是O(n^2)。
评价:
大家也看到上述代码有个标记变量 flag,这是冒泡排序的一种改进,如果在第二次循环中没有发生交换说明排序已经完成,不需要再循环下去了。
选择排序
-
动画演示
-
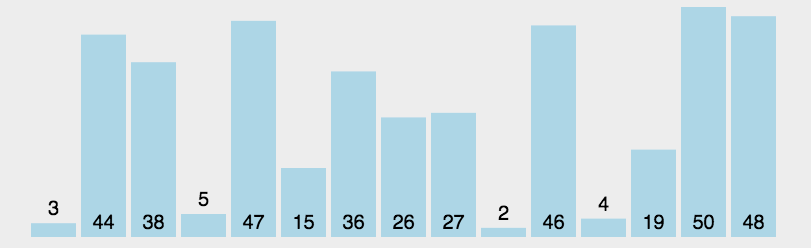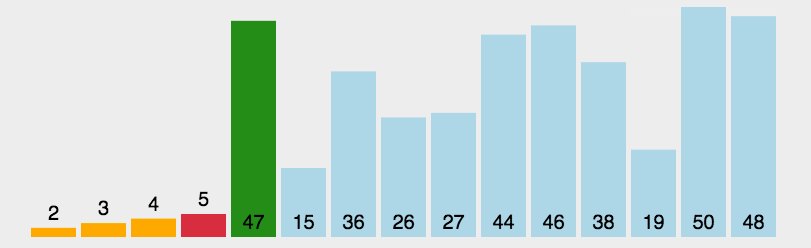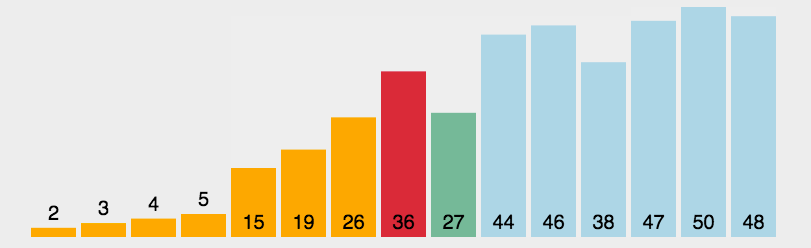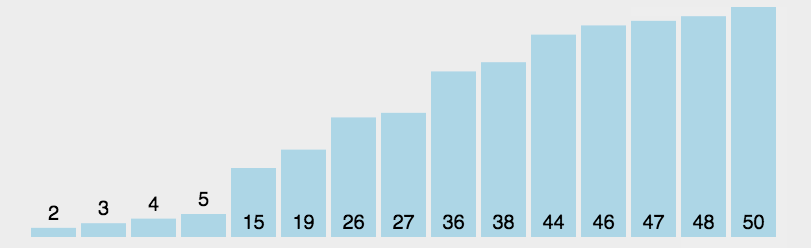
原理
选择排序的原理很简单,就是从需要排序的数据中
选择最小的(从小到大排序),然后放在第一个,选择第二小的放在第二个…… -
代码
// 选择排序,稳定public static void selectSort(int[] a,int n) {for (int i = 0; i < n; i++) {int min=i;for (int j = i+1; j < n; j++) {if(a[min]>a[j]){min = j;}}if (min!=i) {exc(a, i, min);}}} -
分析
时间复杂度:
-
比较的次数: (n-1)+(n-2)+...+1= n(n-1)/2
-
交换的次数: n
评价:
- 运行时间与输入无关,因为前一次的操作,不能为后面提供信息
- 数据的移动次数是最小的
-
高效的比较排序算法
Θ(nlogn)
希尔排序
-
图片演示
-
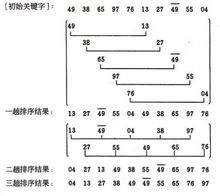
原理
希尔排序是基于插入排序进行改进,又称之为递减增量排序。在前面中我们知道,插入排序是将小的元素往前挪动位置,并且每次只移动一个位置。那么希尔排序是怎么解决这个问题的呢?
希尔排序的理念和梳排序的理念有点类似。在梳排序中,我们比较距离相差为
step的两个元素来完成交换。在希尔排序中,我们的做法也是类似。我们在数组中每隔h取出数组中的元素,然后进行插入排序。当h=1时,则就是前面所写的插入排序了。 -
代码
// 6. 希尔排序public static void shellSort(int[] a, int n) {int h =1;while (h<n/3) {// 数组 1,4,13,40...h = h*3+1;}while (h>=1) {for (int i = h; i < n; i++) {for(int j=i;j>=h&&a[j-h]>a[j];j-=h){exc(a, j, j-h);}}h/=3;}} -
分析
是第一个突破时间复杂度O(n^2)的算法
思路--计算步长,对每次分组进行直接插入排序,减小逆序度
算法时间复杂度在插入排序和快速排序之间
快速排序
-
动画演示
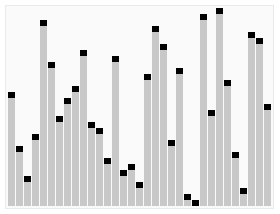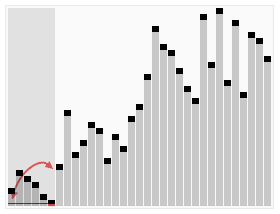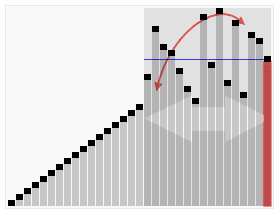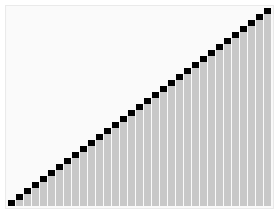
-
原理
快速排序使用了,
Divide and Conquer(分治)策略,不断地把数组分为较大和较小的两个子序列,然后对每个子序列进行递归,直到不可再分。思路就是在拆分的同时进行排序 与归并排序不同。 -
步骤:
-
挑选基准值:从数列中挑出一个元素,称为“基准”(pivot),
-
分割:重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(与基准值相等的数可以到任何一边)。在这个分割结束之后,对基准值的排序就已经完成。
-
递归排序子序列:递归地将小于基准值元素的子序列和大于基准值元素的子序列排序。
递归到最底部的判断条件是数列的大小是零或一,此时该数列显然已经有序。
-
-
代码
// 第一部分public static int partition(int[] a,int l,int h) {int mid = l+((h-l)>>1);int pivot = a[mid];exc(a, l, mid);int i = l;int j = h+1;while (true) {while (a[++i]<pivot) {if(i==h) break;}while (a[--j]>pivot) {if(j==l) break;}if (i>=j) {break;}exc(a, i, j);}exc(a, l, j);return j;}public static void quickSort(int[] a, int n) {quickSort(a, 0, n-1);}// 第二部分public static void quickSort(int[] a, int lo, int h) {if (lo>=h) {return;}int j = partition(a, lo, h);quickSort(a, lo, j-1);quickSort(a, j+1, h);} -
分析
快速排序的最坏时间复杂度为O(n^2),平均时间复杂度为 O(n logn),快速排序基本上被认为是比较排序算法中,平均性能最好的。多种语言皆实现了快速排序的类库。
归并排序
-
动画演示
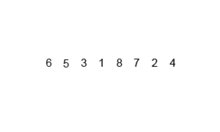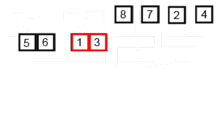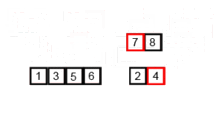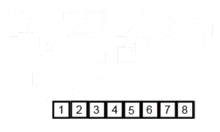
-
原理
采用分治法:
- 分割:递归地把当前序列平均分割成两半。
- 集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。
- 与快速排序不同的是,归并是拆分完成后,在合并阶段进行排序,而
快速排序是边拆分边排序
-
代码
// 第一部分 合并public static void merge(int[] a, int low, int mid, int high) {// 第一种写法int i = low;int j = mid + 1;int k = 0;int[] a2 = new int[high - low + 1];while (i <= mid && j <= high) {if (a[i] < a[j]) {a2[k] = a[i];i++;k++;} else {a2[k] = a[j];j++;k++;}}while (i <= mid) {a2[k] = a[i];i++;k++;}while (j <= high) {a2[k] = a[j];j++;k++;}for (k = 0, i = low; i <= high; k++, i++) {a[i] = a2[k];}}public static void mergeSort(int[] a, int n) {mergeSort(a, 0, n - 1);} // 第二部分 递归 public static void mergeSort(int[] a, int low, int high) {if (low >= high)return;int mid = (high + low) / 2;mergeSort(a, low, mid);mergeSort(a, mid + 1, high);merge(a, low, mid, high);} -
分析
归并排序是一种稳定的且十分高效的排序。时间复杂度总是 O(nlogn),不论好坏,但缺点是,它不是原地排序,占用额外的空间,空间复杂度为 O(n)
堆排序
-
动画演示
-
原理
堆排序是借助堆这一数据结构实现的排序
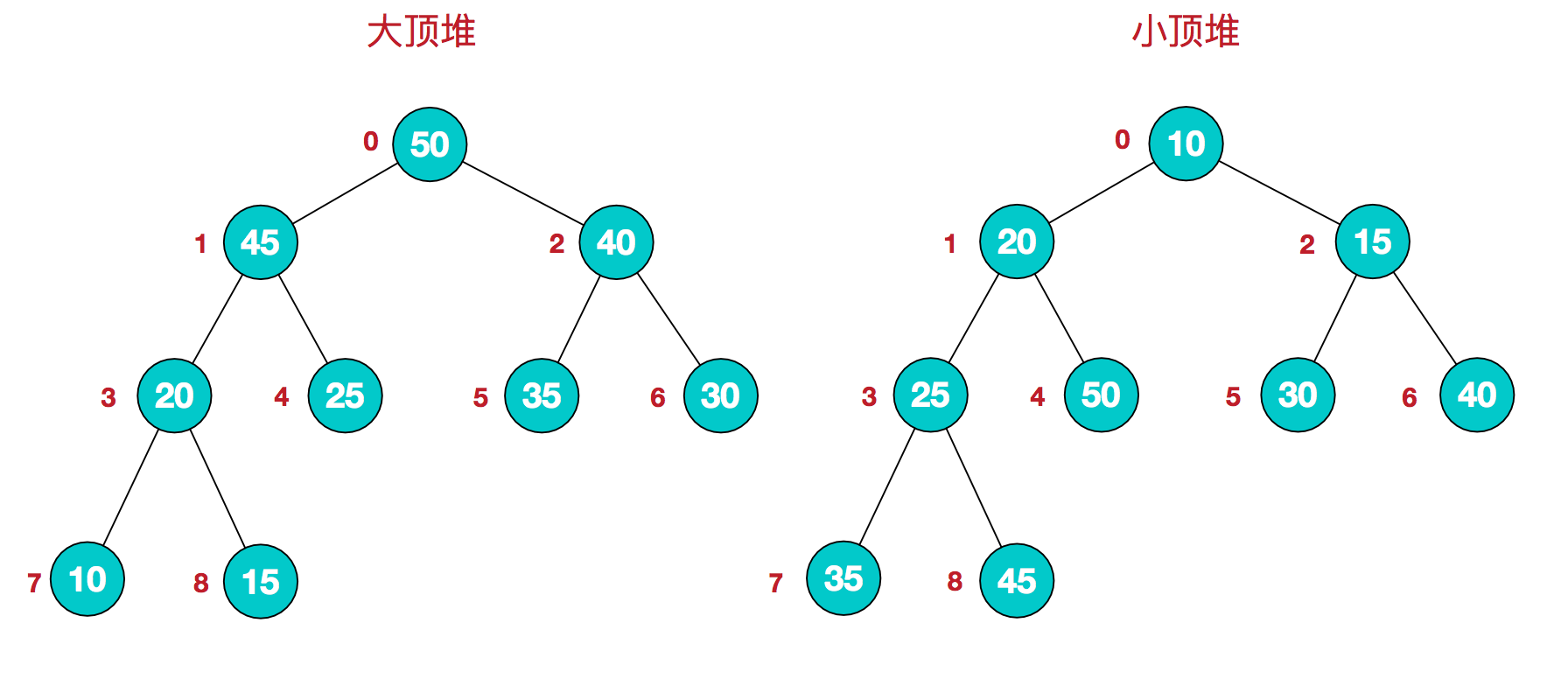
我们利用大顶堆(堆顶元素最大)实现排序,在一个堆中,位置k的结点的父元素的位置是
(k+1)/2-1,而它的两个子节点的位置分别是2k+1和2k+2,这样我们就可以通过计算数组的索引在树中上下移动。思路: 不断把堆顶的元素与最后的元素交换位置,重新堆化,不断得到第k(=1,2,3...)大的元素。相当于一个将大的元素 sink(下沉) 的过程。
-
代码
// 建堆 public static void buildHeap(int[] a, int n) {for (int i = n / 2; i >= 0; i--) {heapify(a, n - 1, i);}} // 堆化 public static void heapify(int[] a, int n, int i) {while (true) {int maxPos = i;if (i * 2 + 1 <= n && a[i] < a[2 * i + 1]) {maxPos = i * 2 + 1;}if (i * 2 + 2 <= n && a[maxPos] < a[i * 2 + 2]) {maxPos = i * 2 + 2;}if (i == maxPos) {break;}exc(a, i, maxPos);i = maxPos;}}public static void heapSort(int[] a, int n) {buildHeap(a, n);int k = n - 1;while (k > 0) {// 交换堆顶元素,把第1,2,3...大元素放到底部exc(a, 0, k);--k;heapify(a, k, 0);}} -
分析
- 时间复杂度一直都是 O(nlogn),不论最好最坏情况。
- 缺点:
- 不稳定算法
- 堆排序的每次排序其数组逆序度都比其他算法高
- 对内存访问不友好(不连续)
牺牲空间的线性排序算法
Θ(n)
计数排序
-
动画演示
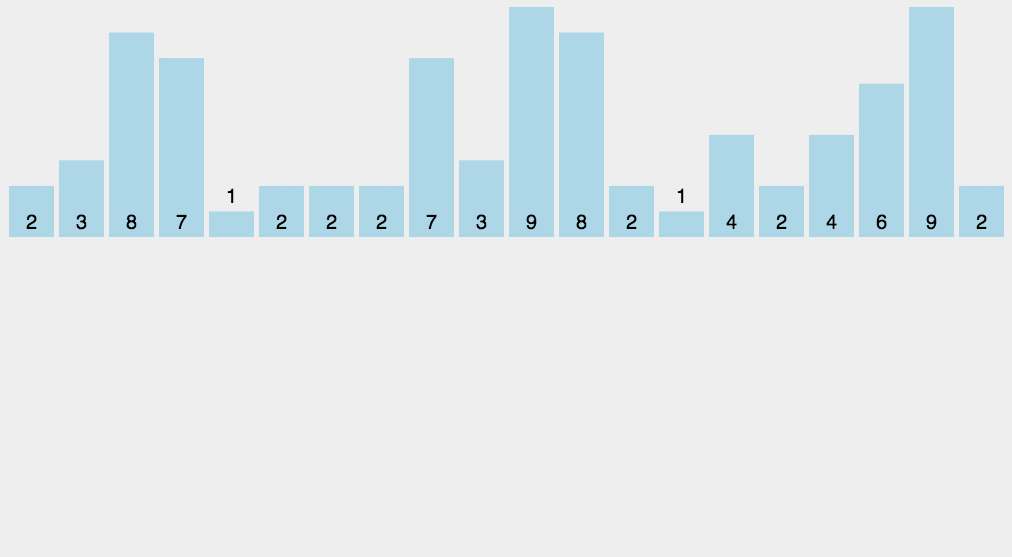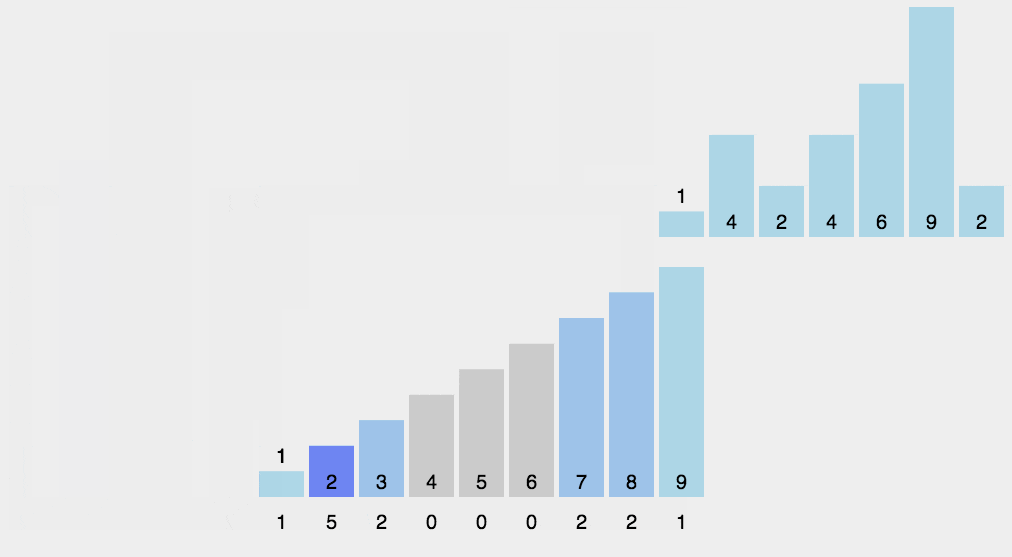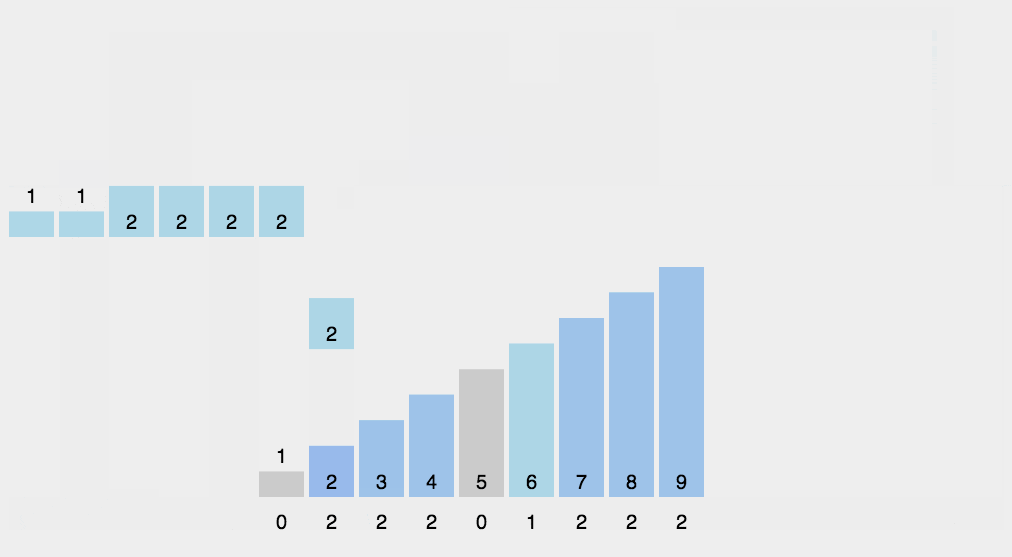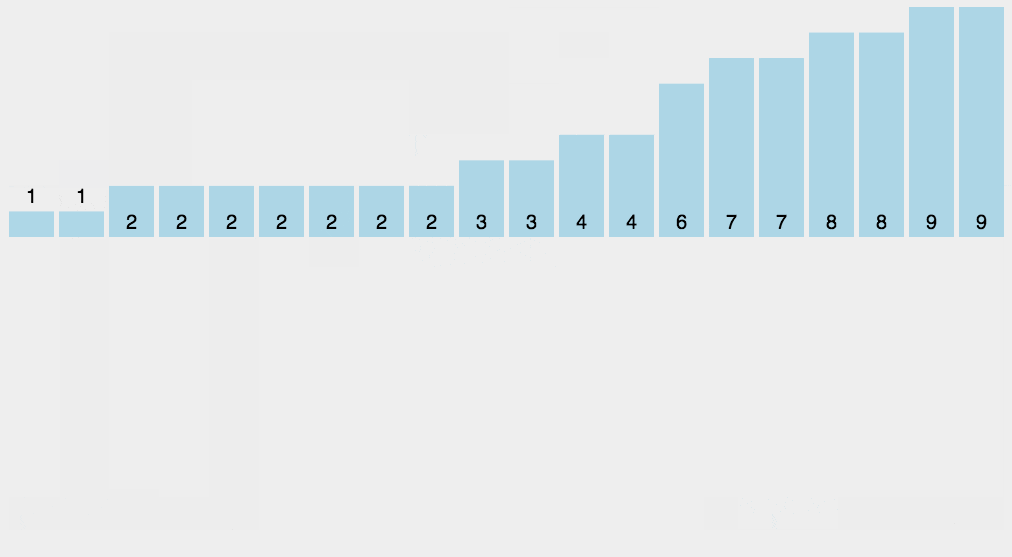
-
原理
计数排序使用一个额外的数组C,其中 C 中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C 来将A中的元素排到正确的位置。
tips:当然,如果数据比较集中的话,我们大可不必创建那么大的数组,我们找出最小和最大的元素,以最小的元素作为基底以减小数组的大小。
-
代码
// 非比较排序public static void countSort(int[] a, int n) {int max = a[0];for (int i = 0; i < n; i++) {if (a[i] > max) {max = a[i];}}int[] c = new int[max + 1];int indexArray = 0;for (int i = 0; i < n; i++) {c[a[i]]++;}for (int i = 0; i <= max; i++) {if (c[i] != 0) {a[indexArray] = i;c[i]--;indexArray++;}}}
桶排序
-
图片演示
-
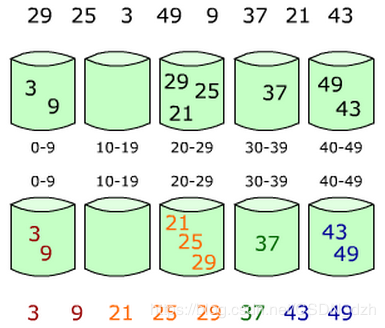
原理
桶排序的基本思想是假设数据在[min,max]之间均匀分布,其中min、max分别指数据中的最小值和最大值。那么将区间[min,max]等分成n份,这n个区间便称为n个桶。将数据加入对应的桶中,然后每个桶内单独排序。由于桶之间有大小关系,因此可以从大到小(或从小到大)将桶中元素放入到数组中。
-
代码
public static void bucketSort(int[] a, int n, int bucketSize) {int max = a[0];int min = a[1];for (int v : a) {if (v > max) {max = v;} else if (v < min) {min = v;}}// 桶的大小int bucketCount = (max - min) / bucketSize + 1;int bucket[][] = new int[bucketCount][bucketSize];int indexArr[] = new int[bucketCount];// 将数字放到对应的桶中for (int v : a) {int j = (v - min) / bucketSize;if (indexArr[j] == bucket[j].length) {ensureCapacity(bucket, j);}bucket[j][indexArr[j]++] = v;}// 每个桶快排// 也可以使用插入保证稳定性int k = 0;for (int i = 0; i < bucketCount; i++) {if (indexArr[i] == 0) {continue;}quickSort(bucket[i], indexArr[i]);for (int j = 0; j < indexArr[i]; j++) {a[k++] = bucket[i][j];}}}// 扩容函数private static void ensureCapacity(int[][] bucket, int j) {int[] tempArr = bucket[j];int[] newArr = new int[tempArr.length * 2];for (int k = 0; k < tempArr.length; k++) {newArr[k] = tempArr[k];}bucket[j] = newArr;} -
分析
桶排序是线性排序的一种,桶排序的核心就是根据数据的范围 (m) ,把数据 (大小为n),尽可能均匀得放到
K个桶里,每个桶再各自实现排序,然后把桶从小到大的列出来,即完成排序。- 时间复杂度 O(N+C),其中C=N*(logN-logK),空间复杂度为 O(N+K)
- 更适用于外部排序,尤其是当 N很大,而M较小时,比如高考排名,分数是固定的,从 0-750分,考生人数很多,用桶排序就能很快得出排名。
基数排序
-
动画演示

-
原理
在日常的使用中,我们接触基数排序比较少,它也是桶排序的一种变形。
它的具体实现分为 LSD (Least sgnificant digital) , MSD (Most sgnificant digital) 两种方法,上面的演示是第一种(LSD),从低位到高位,根据每一位上的数字将元素放入桶中,再按顺序取出,直到比较完最高位,完成排序。
-
代码
/*** * @param x 每一位上的值* @param d 第d位* @param dg 辅助数组* @return 对应的桶的标号*/public static int getDigit(int x, int d, int[] dg) {return (x / dg[d - 1] % 10);}/*** * @param a 待排序数组* @param n 数组长度*/public static void radixSort(int[] a, int n) {// 最大的数int max = 0;int j = 0, i = 0;// 默认十进制final int radix = 10;for (int val : a) {if (val > max) {max = val;}}// 求最大位数int N;if (max == 0) {N = 1;} else {N = (int) Math.log10(max) + 1;}// 设置辅助数组int dg[] = new int[N + 1];for (i = 1, dg[0] = 1; i < N + 1; i++) {dg[i] = 10 * dg[i - 1];}// 初始化桶int bucket[][] = new int[radix][n];int indexArr[] = new int[radix];for (int d = 1; d <= N; d++) {for (int var : a) {j = getDigit(var, d, dg);bucket[j][indexArr[j]++] = var;}int count = 0;for (i = 0; i < radix; i++) {if (indexArr[i] != 0) {for (int k = 0; k < indexArr[i]; k++) {a[count++] = bucket[i][k];}indexArr[i] = 0;}}}} -
分析
时间复杂度为 O(k*n),空间复杂度为O(n),当处理较大(位数多)的数字排序时,比计数排序更好用。
综合分析
-
我们可以看出基于比较的排序算法,他的时间复杂度的最好上界是逼近 O(nlogn) 的,这是因为,比较排序可以看成是决策树,而数组共有 n! 种排列方式,根据 斯特林公式 比较排序的时间复杂度的最好上界是接近于 nlogn的
-
我们可以看出基于非比较排序的线性时间排序的思路,大致相同,都是找到与元素匹配的桶,完成排序。都是空间换时间的思想。
文章最后,感谢大家的阅读,文中若有错漏之处,请在留言区积极指出,十分欢迎大家一起交流讨论!
另外感谢朋友们的支持,友情链接 。








