绵阳网络公司网站建设/网络平台推广是干什么

谈论算法，典型的问题除了排序，还有查找。

查找就是，从一个数据集合中查找某个数，如果找到了就返回该数据在数据集中的索引，否则返回 -1。

最简单的方法就是从头到尾依次查找。

但这有个问题，顺序查找时间复杂度是$O(n)$，如果要从 1 亿个数据中查找某个数，最坏的情况要查找 1 亿次。

那么有没有更快速的算法呢？

答案是有的，这篇文章讲的二分查找就是这样一种，它的时间复杂度是$O(lo{g}_n)$ 。

猜数字

我们小时候都玩过这样的游戏。

对方在心里默念一个数字。

然后，叫你猜。

你说： 42.

他说： 小了。

你说： 78

他说： 大了

你说： 64

他说： 小了

你说： 70

他微笑不语。

实际上，二分查找的逻辑和这个无异。

算法图例

假如要从下面的有序数组中查找 25 。

arr = [1,3,16,23,25,32,79]

二分查找的思路就是每一次都和数组中的中间数据比较，不断缩小候选数据集的范围

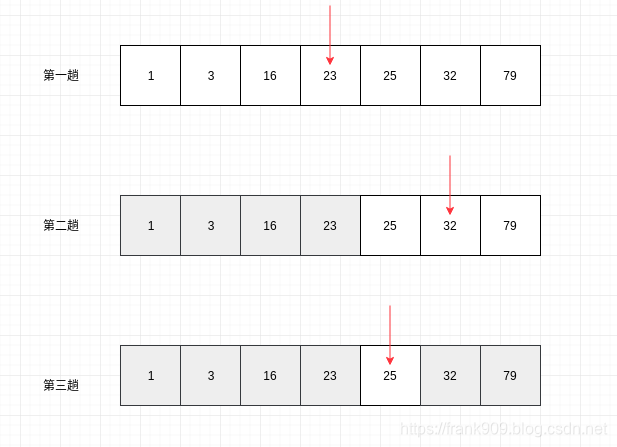
上面的图例清晰明了。

因为每次查找都缩减了范围，所以数据集会折半。

折半的概念用数学符号表示就是$lo{g}_n$,当然是以 2 对底数。

Python 代码

def binary_search(arr,value):result = -1low = 0high = arr.__len__()while low <= high:middle = int ((high - low)/2) + lowif arr[middle] == value:return middle elif arr[middle] < value:# searching in right sub listlow = middle + 1elif arr[middle] > value:# searching in left sub listhigh = middle - 1return resultif __name__ == "__main__":arr = [1,3,16,23,25,32,79]print("=======================")print(arr)result = binary_search(arr,25)print("=======================")print(result)result = binary_search(arr,16)print("=======================")print(result)result = binary_search(arr,15)print("=======================")print(result)

代码结果：

=======================
[1, 3, 16, 23, 25, 32, 79]
=======================
4
=======================
2
=======================
-1

代码比较简单，核心就是控制 low 和 high 两个游标不停地缩小选择范围。

如果什么都没有找到就返回 -1.

值得注意的是，二分查找法适用与有序数组。如果是无序的就不能操作。并且如果数据用链表形式也比较麻烦。